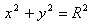Кто открыл уравнение окружности

1. Уравнение окружности.
2. Исторические данные.
3. Повторение пройденного материала.

Видео:Уравнение окружности (1)Скачать

Уравнение окружности

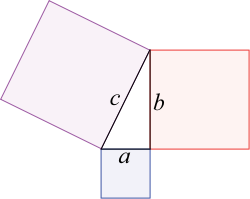
Самым простым из способов, представляющих уравнения окружности, является теорема Пифагора.

Вы уже знаете, что теорема Пифагора имеет как геометрическую формулировку, так и алгебраическую.

Геометрическая формулировка звучит так:

В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Алгебраическая формулировка звучит так:

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

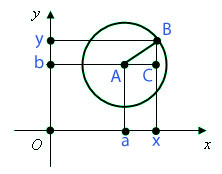
Давайте возьмем окружность, центром которой является точка A (a; b) и радиус R. Теперь давайте на этой окружности возьмем произвольную точку В (x; y). В этом случае мы с вами можем применить теорему Пифагора.

В итоге, как видно с рисунка, мы с вами получили прямоугольный треугольник, который имеет стороны: АВ, ВС и СА.

В том случае, когда центр окружности расположен в начале координат, то есть, a = 0 и b = 0, то мы получаем уравнение окружности, которое принимает такой вид:

Обратно: любая точка В, координаты которой удовлетворяет данному уравнению окружности, принадлежат окружности.

Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Немного истории

А знаете ли вы, что оказывается термины «окружность» и «круг» получили свои названия еще во времена Древней Греции. Для древних греков окружность и круг были венцом совершенства, ведь они уже в те времена пришли к выводу, что окружность в каждой своей точке устроена таким образом, что позволяет ей двигаться самой по себе. Также они обратили внимание на то, что из всех фигур, которые имеют одинаковую длину периметра, только у круга наибольшая площадь.

Древние философы придавали огромное значение окружности, ведь она является одной из древнейших геометрических фигур. Если следовать учению Аристотеля, то все планеты и звезды нашей вселенной движутся по самой совершенной линии, которой является окружность. Да и еще на протяжении сотни лет ученые астрономы были уверены, что все планеты движутся по окружности. И лишь только в XVII веке учением Коперника, Галилея, Кеплера и Ньютона это суждение было опровергнуто.

Аристотель

Николай Коперник

Галилео Галилей

Иоганн Кеплер

Исаак Ньютон

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Повторение ранее изученного материала

Даже в древние времена круглые предметы вызывали огромный интерес у человека, так как тогда отсутствовали какие-либо технические сооружения, и для постройки знаменитых египетских пирамид приходилось использовать бревна круглой формы. Немного позже для перемещения огромных глыб, вместо бревен стали использовать колеса, так как они были легче в использовании.

Видео:ПРОСТОЙ СЕКРЕТ ДЛЯ НАЧИНАЮЩИХ! Реши алгебру за 12 минут — Уравнение ОкружностиСкачать

Геометрические примитивы

А теперь давайте вспомним, какие примитивные фигуры вы уже изучили и дадим им определения.

Вы уже знаете, что любой фигурой называют произвольное множество точек на плоскости.

К таким геометрическим фигурам можно отнести точку, прямую, отрезок, луч, треугольник, круг, квадрат и др.

Также вам известно, что точка и прямая являются основными геометрическими фигурами на плоскости. Но в геометрии этим фигурам не дается определения, и они являются неопределяемыми геометрическими фигурами на плоскости.

Как правило, точки обозначаются заглавными латинскими буквами: А, В, С, D …. А вот прямые, обозначаются латинскими строчными буквами: а, b, с, d ….

«Точка» является одним из основных понятий в геометрии, но определения она не имеет. По теории Евклида, точкой является то, что нельзя разделить.

«Прямая» также является одним из главных геометрических понятий. Она представляет собой линию, которая незамкнутая, не искривленная и протяженная с двух сторон, у которой поперечное сечение стремится к нулю, а продольная проекция на плоскость даёт точку.

«Треугольник» является также простейшей геометрической фигурой, которая имеет три стороны и три угла. Можно сказать, что это такая часть плоскости, которая ограничена тремя точками, и тремя отрезками, которые попарно соединяют эти точки.

«Прямоугольник» является параллелограммом, с четырьмя углами, каждый из которых равен 90 градусам.

«Окружность» — это такая геометрическая фигура, у которой каждая точка равноудалена от центра окружности.

Видео:УРАВНЕНИЕ ОКРУЖНОСТИ 8 и 9 класс геометрияСкачать

Связь окружности с другими фигурами

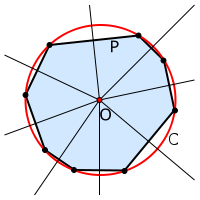
Так как вы уже изучали тему «Окружность», то вам известно, что описанной окружностью многоугольника является такая окружность, которая охватывает все вершины этого многоугольника.

Если вы внимательно рассмотрите рисунок, то увидите, что центром пересечения серединных перпендикуляров окружности является точка О.

А вот вписанной в многоугольник окружностью называют такую окружность, которая расположена внутри данного многоугольника и которая касается всех прямых, проходящих через его стороны.

Видео:УРАВНЕНИЕ ОКРУЖНОСТИСкачать

Прямоугольная система координат

Изображенная на рисунке система координат называется декартовой или прямоугольной. Первое свое название эта система координат получила благодаря имени своего создателя, а вторая, благодаря прямому углу, который равен 90°.

Видео:УРАВНЕНИЯ ОКРУЖНОСТИ И ПРЯМОЙ 9 класс геометрияСкачать

Окружность и круг

А теперь давайте с вами вспомним все определения, которые непосредственно касаются таких понятий, как «окружность» и «круг».

Окружностью называют такую замкнутую прямую линию, у которой все точки равноудалены от центра.

А кругом является та часть плоскости, которая ограниченная этой окружностью.

Но мы с вами также знаем, что каждая окружность имеет диаметр. Им называют отрезок, соединяющий две точки окружности. Диаметр проходит через центр этой окружности и является максимальным расстоянием между точками этой фигуры.

Радиус окружности делит диаметр пополам, а также соединяет центр окружности с любой его точкой.

В отличие от диаметра, хорда не проходит через центр окружности, а располагается около нее.

В окружности присутствует и такое понятие, как круговой сектор. Это часть круга, которая ограничивается дугой и двумя радиусами. Эти радиусы соединяют концы дуги с центром круга.

Ну и, как правило, в геометрии для построения окружности используют циркуль.

Видео:Уравнение окружности | Геометрия 7-9 класс #90| ИнфоурокСкачать

Интересный факт

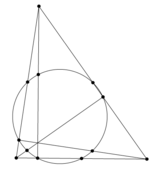
Окружность девяти точек

Такой простой, на первый взгляд многоугольник, который является треугольник издавна не оставлял равнодушными многих ученых математиков. Уделил свое внимание этой фигуре и такой знаменитый математик, как Леонард Эйлер. Он вывел и доказал теорему окружности девяти точек. В геометрии треугольника это обозначает, что есть окружность, которая проходит через середины всех имеющихся сторон треугольника. Такая окружность получила название окружности «Эйлера», «Фейербаха» или окружности шести точек.

Окружностью девяти точек она называется благодаря следующей теореме:

В 1765 году Леонард Эйлер представил доказательство того, что основания высот и середины сторон расположены на одной окружности. Благодаря этому доказательству и появилось название «окружность шести точек».

Но это доказательство еще носит имя Карла Фейербаха, так как он первым его опубликовал в 1821 году вместе с теоремой, которой дал свое имя.

Видео:Составить уравнение окружности. Геометрия. Задачи по рисункам.Скачать

Урок по геометрии по теме: «Уравнение фигуры. Уравнение окружности»
презентация к уроку по геометрии (9 класс)

Презентации по геометрии за 9 класс по теме: » Уравнение фигуры. Уравнение окружности»

Видео:УРАВНЕНИЕ ОКРУЖНОСТИ. ЗАДАНИЕ 18 (С5). АРТУР ШАРИФОВСкачать

Скачать:

Предварительный просмотр:

Видео:Уравнение окружности и формула расстояния между точками на плоскостиСкачать

Подписи к слайдам:

Уравнение фигуры. Уравнение окружности составила учитель математики Веселова С.М.

1.Как называется геометрическая фигура, состоящая из множества всех точек, равноудаленных от данной точки? 2. Как называется точка равноудаленная от всех точек окружности? O 1. Окружность 2. Центр окружности

3.Как называется хорда, проходящая через центр окружности? O 3. Диаметр B A

4. Как называется отрезок, соединяющий центр окружности с точкой на окружности? O 4. Радиус M r

5.Чему равно расстояние между точками А и В?

Какая фигура является графиком уравнения? С. у = 2х-1 В. у = А. у = Рис. 1 Рис. 2 Рис. 3 А В С 3 1 2

Уравнение у=2х-1 является уравнением прямой т. А (0;-1) и т. В(2;3) лежат на прямой т. С (2;2) не лежит на прямой Уравнением фигуры F, заданной на плоскости xy , называют уравнение с двумя переменными x и y, обладающее следующими свойствами: 1) если точка принадлежит фигуре F, то ее координаты являются решением данного уравнения; 2) любое решение (x; y) данного уравнения является координатами точки, принадлежащей фигуре F.

пример А (2;4) – центр, R = 3, то ( х – 2 ) 2 + ( у – 4 ) 2 = 3 2 ; ( х – 2 ) 2 + ( у – 4 ) 2 = 9 . уравнение окружности

Пример 1: Напишите уравнение окружности (0;0) – центр окружности, R- радиус ( х – а ) 2 + ( у – b ) 2 = R 2 . ( х – 0 ) 2 + ( у – 0 ) 2 = R 2 , х 2 + у 2 = R 2 − уравнение окружности с центром в начале координат. Пример: 2 О (0;0) – центр, R = 5 , тогда х 2 + у 2 = 5 2 ; х 2 + у 2 = 25 . Для того чтобы составить уравнение окружности, нужно: 1) узнать координаты центра; 2) узнать длину радиуса; 3) подставить координаты центра ( а ; b ) и длину радиуса R в уравнение окружности ( х – а ) 2 + ( у – b ) 2 = R 2 .

(Задание выполняется Устно) Уравнение окружности Центр радиус ( x – 3 ) 2 + ( y – 2) 2 = 16 C ( 3; 2) r = 4 ( x – 1 ) 2 + ( y + 2) 2 = 4 C ( 1;-2) r = 2 ( x + 5 ) 2 + ( y – 3) 2 = 25 C ( -5; 3) r = 5 x 2 + ( y + 2) 2 = 2 C ( 0;-2) x 2 + y 2 = 9 C ( 0; 0) r = 3

Уравнение окружности Центр радиус ( x – 1 ) 2 + ( y – 2) 2 = 6 4 C ( 1; 2) r = 8 ( x – 1 ) 2 + ( y + 2) 2 = 0,64 C ( 1;-2) r = 0,8 ( x + 5 ) 2 + y 2 = 1,44 C ( -5; 0) r = 1,2 x 2 + y 2 = 5 C ( 0; 0) ( x + 6) 2 + ( y + 2) 2 = 7 C ( -6;-2)

Решение задач с записью в тетради № 330 ( а,б ), № 332

Что называют уравнением фигуры, заданной на плоскости ху ? Какой вид имеет уравнение окружности с центром в точке (а; b) и радиусом R ? Какой вид имеет уравнение окружности с центром в начале координат и радиусом R ?

П.9 читать, знать все определения и формулы наизусть, № 329, № 331, № 333

Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

окружность

Определение: Окружность — это линия второго порядка, которая представляет собой геометрическое место точек плоскости, равноудаленных от одной заданной точки, называемой центром.

Если центр находится в начале координат, то окружность задается каноническим уравнением второй степени вида: х2+у2=R2 , где R — радиус окружности; х,у — текущие координаты точек, лежащих на окружности.

Для вывода данного уравнения возьмем на окружности произвольную точку М(х;у). Отрезок ОМ=R является гипотенузой в прямоугольном треугольнике ОМР, а катеты определяются координатами х и у точки М. Уравнение окружности получается по теореме Пифагора: х2+у2=R2, которое называется каноническим уравнением окружности с несмещенным центром.

Если центр окружности находится в точке С(х0;у0), то уравнение окружности со смещенным центром будет иметь

Построение окружности выполняется с помощью циркуля.

Видео:Уравнение окружностиСкачать

эллипс

Определение: Эллипс — это линия второго порядка, которая представляет собой геометрическое место точек плоскости, сумма расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная и равная большой оси эллипса.

Эллипс с несмещенным центром задается каноническим уравнением второй степени вида:

где а и в — полуоси, х,у — текущие координаты точек, лежащих на эллипсе. Центр симметрии находится в начале координат. Осями симметрии служат координатные оси.

При рассмотрении эллипса возможны два случая:

• 1. Если ав, то а называется большая полуось, лежащая на координатной оси Ох, а в — малая полуось, лежащая на координатной оси Оу;
• 2. Если ав, то а называется малая полуось, лежащая на координатной оси Ох, а в-большая полуось, лежащая на координатной оси Оу.

Фокусы F1 и F2 всегда лежат на большой оси эллипса, причем симметрично относительно центра симметрии на расстоянии:

где величина «с» определяет фокусное расстояние.

Для характеристики формы эллипса вводится эксцентриситет.

Определение: Эксцентриситетом эллипса называется отношение фокусного расстояния к длине его большой полуоси:

=, если ав и =, если ва.

Значение эксцентриситета меняется в пределах 0??1. При этом форма эллипса изменяется от окружности (е=0, при а=в=R) и, вытягиваясь, вырождается в прямую (е=1, при а>>в).

Уравнение эллипса выводится из его основного свойства, представленного в определении. Возьмём на эллипсе произвольную точку М(х;у). Расстояния r1 и r2 от фокусов F1 и F2 до точки М(х;у) называются фокальными радиусами.

В соответствии с определением сумма фокальных радиусов есть величина постоянная, равная большой оси эллипса: r1 + r2 = 2а (при ав) — основное свойство эллипса. Для вывода уравнения эллипса необходимо выразить фокальные радиусы r1 и r2 через координаты точки М(х;у) и фокусов F1(с;0) и F2(-с;0)и подставить в это равенство.

Если центр симметрии смещен и находится в точке С(х0;у0), то уравнение эллипса со смещенным центром имеет вид:

Построение эллипса рассмотрим ниже на примерах.

Пример. Определить вид, параметры и построить линию, заданную уравнением:

Решение: 1. Это эллипс с несмещенным центром вида:

2. Найдем параметры: — большая полуось на оси Ох;

— малая полуось на оси Оу;

Фокусы F1(4.6;0) и F2(-4.6;0) лежат на большой оси, совпадающей с осью Ох, симметрично, на расстоянии с=4.6 относительно начала координат.

• 3. Построение эллипса (см. рисунок выше) выполним по этапам:
• 1) строим систему координат Оху;
• 2) на координатных осях симметрично относительно начала координат откладываем большую и малую полуоси (а=5, в=2) и показываем вершины эллипса А1,А2,В1,В2;
• 3) через вершины эллипса параллельно координатным осям строим осевой прямоугольник;
• 4) вписываем эллипс в осевой прямоугольник;
• 5) на большой оси, совпадающей с осью Ох, симметрично относительно начала координат показываем фокусы F1(4.6;0) и F2(-4.6;0).

📺 Видео

№969. Напишите уравнение окружности с диаметром MN, если: а) М (-3; 5),Скачать

Составляем уравнение окружностиСкачать

Уравнение окружности. Практика. Урок 7. Геометрия 9 классСкачать

Геометрия 9 класс (Урок№9 - Уравнение линии на плоскости. Уравнение окружности. Уравнение прямой.)Скачать

Уравнение окружности ? Окружность в системе координат / Функция окружностиСкачать

8 класс. Геометрия. Уравнение окружности.Скачать