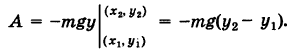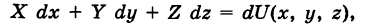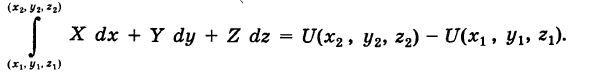Если дан криволинейный интеграл, а кривая, по которой происходит интегрирование — замкнутая (называется контуром), то такой интеграл называется интегралом по замкнутому контуру и обозначается следующим образом:

Область, ограниченную контуром L обозначим D. Если функции P(x, y) , Q(x, y) и их частные производные 


Таким образом, вычисление криволинейного интеграла по замкнутому контуру сводится к вычислению двойного интеграла по области D.
Формула Грина остаётся справедливой для всякой замкнутой области, которую можно проведением дополнительных линий на конечное число простых замкнутых областей.
Пример 1. Вычислить криволинейный интеграл

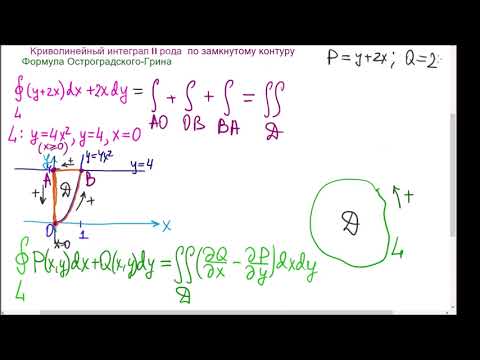
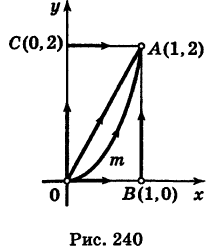
если L — контур треугольника OAB , где О(0; 0) , A(1; 2) и B(1; 0) . Направление обхода контура — против часовой стрелки. Задачу решить двумя способами: а) вычислить криволинейные интегралы по каждой стороне треугольника и сложить результаты; б) по формуле Грина.
а) Вычислим криволинейные интегралы по каждой стороне треугольника. Сторона OB находится на оси Ox , поэтому её уравнением будет y = 0 . Поэтому dy = 0 и можем вычислить криволинейный интеграл по стороне OB :
Уравнением стороны BA будет x = 1 . Поэтому dx = 0 . Вычисляем криволинейный интеграл по стороне BA :
Уравнение стороны AO составим, пользуясь формулой уравнения прямой, проходящей через две точки:

Таким образом, dy = 2dx . Вычисляем криволинейный интеграл по стороне AO :
Данный криволинейный интеграл будет равен сумме интегралов по краям треугольника:

б) Применим формулу Грина. Так как 


Как видим, получили один и тот же результат, но по формуле Грина вычисление интеграла по замкнутому контуру происходит значительно быстрее.
Пример 2. Пользуясь формулой Грина, вычислить криволинейный интеграл

где L — контур OAB , OB — дуга параболы y = x² , от точки О(0; 0) до точки A(1; 1) , AB и BO — отрезки прямых, B(0; 1) .
Решение. Так как функции 



Пример 3. Пользуясь формулой Грина, вычислить криволинейный интеграл

Решение. Линия y = 2 − |x| состоит из двух лучей: y = 2 − x , если x ≥ 0 и y = 2 + x , если x .
Имеем функции 



Пример 4. С помощью формулы Грина вычислить криволинейный интеграл

если L — окружность 
Решение. Функции 




- Криволинейный интеграл вдоль треугольника
- Контакты
- Криволинейные интегралы — определение и вычисление с примерами решения
- Криволинейные интегралы
- Криволинейный интеграл первого рода
- Физический смысл криволинейного интеграла второго рода
- Условие независимости криволинейного интеграла второго рода от вида пути интегрирования
- Работа потенциальной силы
- 📹 Видео
Видео:Криволинейный интеграл II рода вдоль плоской кривойСкачать

Криволинейный интеграл вдоль треугольника
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
 |
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Двойные и тройные интегралы
- Делимость чисел в математике
- Обыкновенные дроби
- Отношения и пропорции
- Уравнения поверхности и линии в пространстве
- Общее уравнение плоскости
- Угол между плоскостями
- Понятие о производной вектор-функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📹 Видео
Формула ГринаСкачать

Криволинейный интеграл 1 родаСкачать

Криволинейный интеграл по длине дуги ➜ Криволинейный интеграл 1-го родаСкачать

Формула Остроградского - ГринаСкачать
Криволинейный интеграл 1-го рода ★ Криволинейный интеграл по длине дуги ★ ∫(x+y)dsСкачать

Формула ГринаСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Криволинейный интеграл 2 родаСкачать

Криволинейный и двойной интеграл. Формула Грина.Ч1Скачать

Криволинейные интегралыСкачать

Криволинейный интеграл 1 рода.Скачать
Формула Стокса.ЦиркуляцияСкачать

Циркуляция векторного поля. Вычисление при при помощи криволинейного интеграла.Скачать

Непосредственное вычисление циркуляцииСкачать

Криволинейный интеграл II рода по пространственной кривойСкачать

Криволинейный интеграл первого родаСкачать












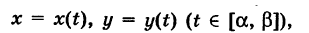
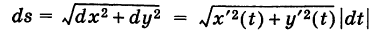
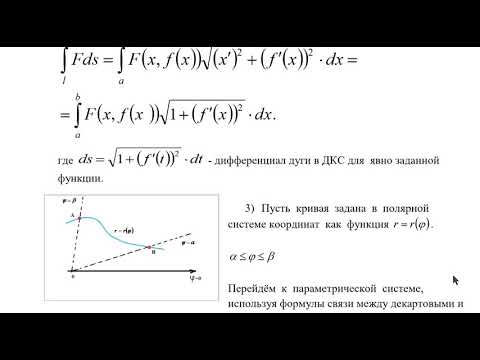
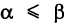 , то dt > 0 и
, то dt > 0 и 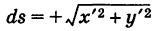 ; если же
; если же  , то dt 2 . Так как парабола проходит через точку
, то dt 2 . Так как парабола проходит через точку 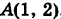 , то 2 = k — 1 2 и, значит, k = 2, т. е. у = 2х 2 . Отсюда dу = 4х dx и
, то 2 = k — 1 2 и, значит, k = 2, т. е. у = 2х 2 . Отсюда dу = 4х dx и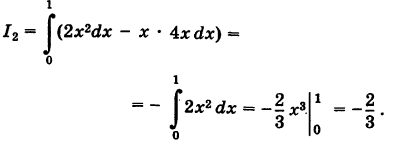
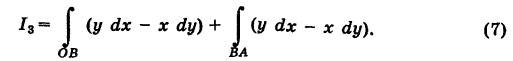
 , то
, то  = 0. Далее, уравнение ВА записывается так: х = 1
= 0. Далее, уравнение ВА записывается так: х = 1 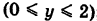 ; поэтому х'(у) = 0. Из формулы (7) получаем
; поэтому х'(у) = 0. Из формулы (7) получаем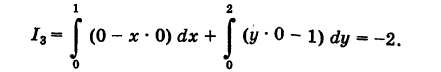
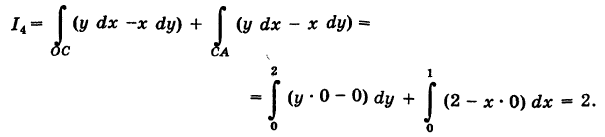
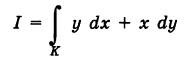
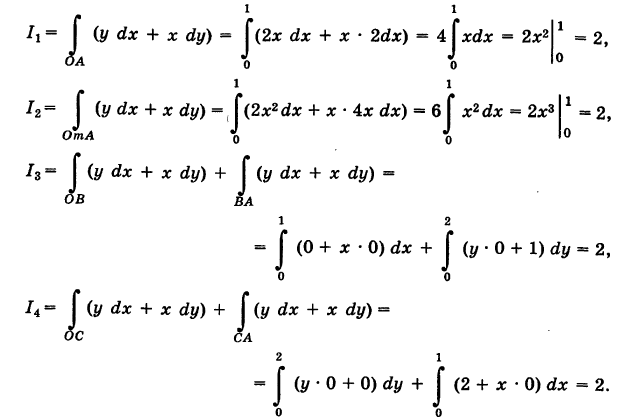
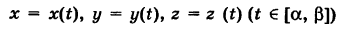
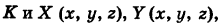
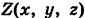 — тройка функций, непрерывных на кривой К, то под соответствующим криволинейным интегралом второго рода понимается интеграл
— тройка функций, непрерывных на кривой К, то под соответствующим криволинейным интегралом второго рода понимается интеграл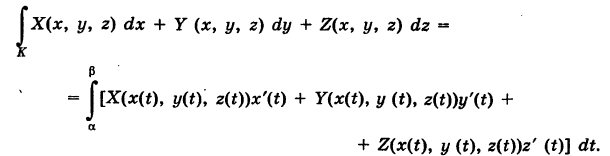
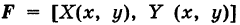 — непрерывно меняющаяся переменная сила и
— непрерывно меняющаяся переменная сила и
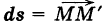 бесконечно малый вектор перемещения из текущей точки М (х, у) кривой К в бесконечно близкую точку
бесконечно малый вектор перемещения из текущей точки М (х, у) кривой К в бесконечно близкую точку 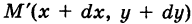 (мы здесь пренебрегаем бесконечно малыми высшего порядка по сравнению с ds). Имеем ds = . Так как на бесконечно малом пути ds непрерывную силу F можно считать постоянной, то элементарная работа силы равна
(мы здесь пренебрегаем бесконечно малыми высшего порядка по сравнению с ds). Имеем ds = . Так как на бесконечно малом пути ds непрерывную силу F можно считать постоянной, то элементарная работа силы равна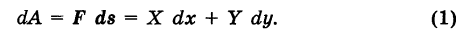
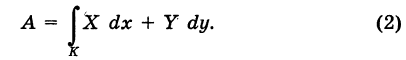
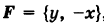 , точка приложения которой описывает параболу ОВ (рис. 242)
, точка приложения которой описывает параболу ОВ (рис. 242)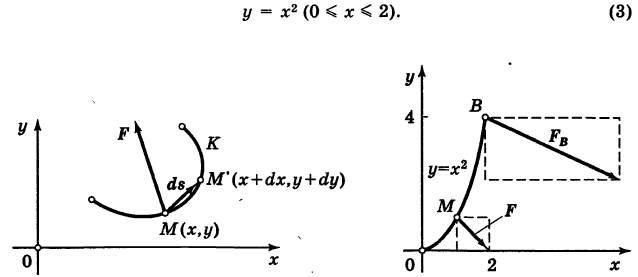
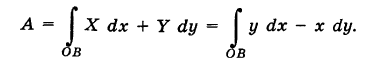
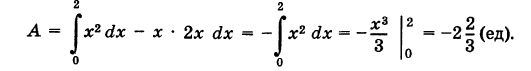
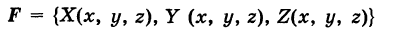
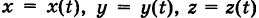 выражается криволинейным интегралом второго рода
выражается криволинейным интегралом второго рода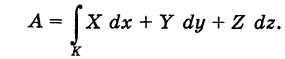
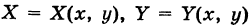 — непрерывные функции в области G (рис. 243). Рассмотрим две произвольные точки
— непрерывные функции в области G (рис. 243). Рассмотрим две произвольные точки 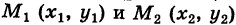 области и всевозможные пути
области и всевозможные пути 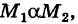
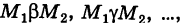 соединяющие эти точки (М1 — начало пути, М2 — конец пути) и не выходящие за пределы области G. Может случиться, что
соединяющие эти точки (М1 — начало пути, М2 — конец пути) и не выходящие за пределы области G. Может случиться, что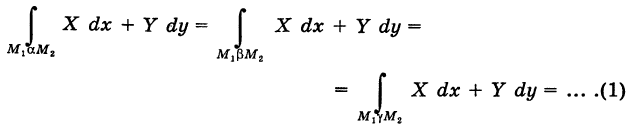
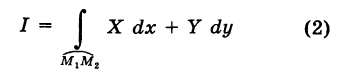
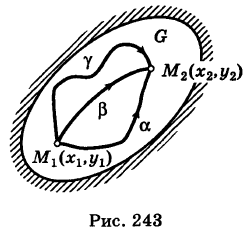
 и его конечную точку М2
и его конечную точку М2  пути. Поэтому здесь употребляется обозначение
пути. Поэтому здесь употребляется обозначение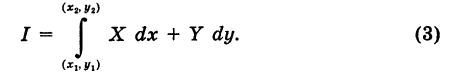
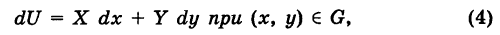
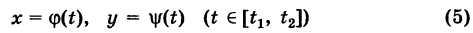
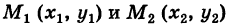 , причем
, причем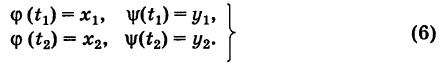
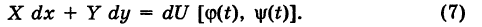
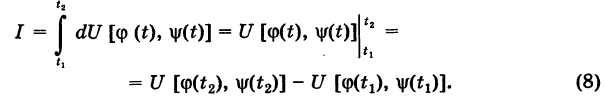
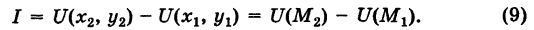
 , и, следовательно, интеграл I не зависит от вида пути, соединяющего точки
, и, следовательно, интеграл I не зависит от вида пути, соединяющего точки 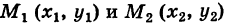
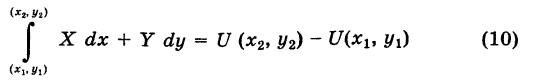
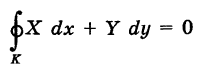
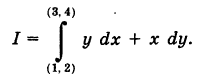
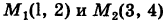 , имеем
, имеем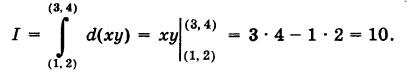
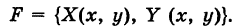
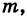 находящуюся на расстоянии г от притягивающего центра, согласно закону Ньютона действует сила
находящуюся на расстоянии г от притягивающего центра, согласно закону Ньютона действует сила 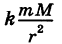 (k — гравитационная постоянная), направленная к притягивающему центру. Другим примером силового поля служит электрическое поле Кулона.
(k — гравитационная постоянная), направленная к притягивающему центру. Другим примером силового поля служит электрическое поле Кулона.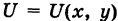 такая, что
такая, что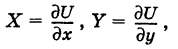
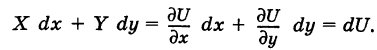
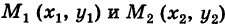 , имеем
, имеем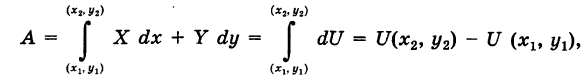
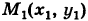 в положение
в положение 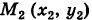 (рис. 244).
(рис. 244).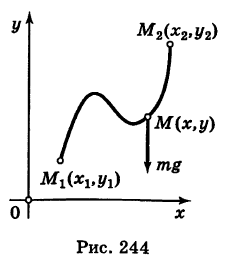
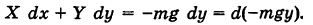
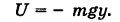
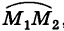 , равна
, равна