Корень из трех на числовой окружности

Сейчас я вам что покажу, закачаетесь. Обязательно загляните под кат, самые интересные картинки я припрятал там.

Я продолжаю рассказ о применении философской геометрии на практике. Прошлая часть была обзорная, она говорила о том, что многие века геометрия использовалась для поиска универсальных идеальных законов природы. Эти законы повсеместно использовались в произведениях искусства, архитектуре и духовной жизни.

Сегодня я расскажу про замечательную пропорцию «корень из трех». Я покажу ее сакральный смысл, а под катом продемонстрирую пример из современного дизайна, который повергнет вас в шок 😉

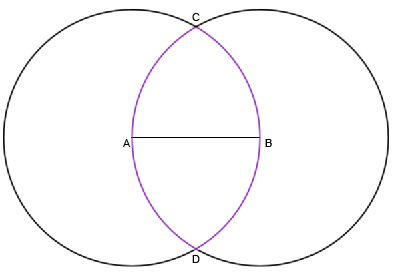
Начнем с построения пропорции. Возьмем отрезок AB.

Примем его за радиус и построим окружность с центром в A.

Теперь построим вторую окружность с тем же радиусом, но с центром в B.

У нас получилась фигура ACBD, имеющая огромное значение для наших предков. Она называется Vescica Piscis (пузырь рыбы). Самый простой и важный пример — она давно является символом христианства.

Я продолжу под катом. Спорим, никогда не догадаетесь чем там все закончится 🙂

Ну вот, раз мы уже под катом, начну сыпать картинки. Мы остановились на Vescica Piscis и символе христианства. Вот Христос вписан в эту фигуру.

Вот здесь изображено много символической рыбы.

Кстати, впервые я про это узнал, купив вот такую подвеску в Кафедральном соборе Уппсалы. Так что символ вполне используется и сейчас.

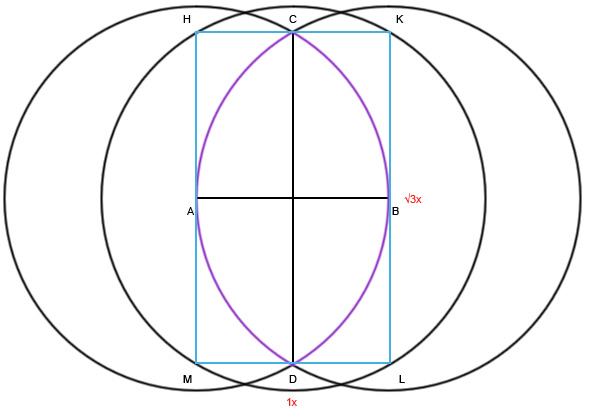
Но чем же так примечательна фигура? Давайте вернемся к построениям. Соединим точки C и D, а из места их пересечения нарисуем еще одну окружность с радиусом AB. Нарисуем прямоугольник HKLM.

Этот прямоугольник обладает замечательным свойством. Его высота относится к ширине ровно как корень их трех (√3 / 1). Корень из трех — это одно из основных иррациональных чисел, но основе которых строилось множество картин, зданий и просто предметов.

Но если вы думаете, что это все старо, уныло и протухло, то вы ошибаетесь. Я обещал сюрприз. Готовы? Только громко не смейтесь.

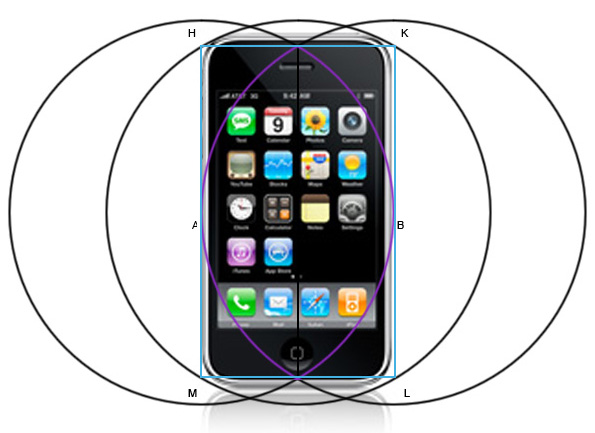
Да-да, это он. iPhone не идеально помещается в этот прямоугольник, но его размеры чрезвычайно близки. Мне кажется что это не совпадение вот почему.
Корень из трех — это примерно 1.732050…
Отношение сторон айфона первого поколения (115×61) примерно равно 1.88524.
iPhone 3G (115.5×61.8) — 1.8599
iPod Touch (110×61.8) — 1.779

Смотрите, они стремятся к идеалу! Мешать им могут только тысячи технических причин.

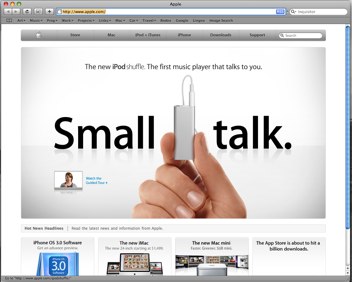
Удивлены? Смущены? Не верите? Сейчас будет больше. Зайдем на apple.com

Хм… Что-то мне этот центральный блок напоминает. А ну ка…

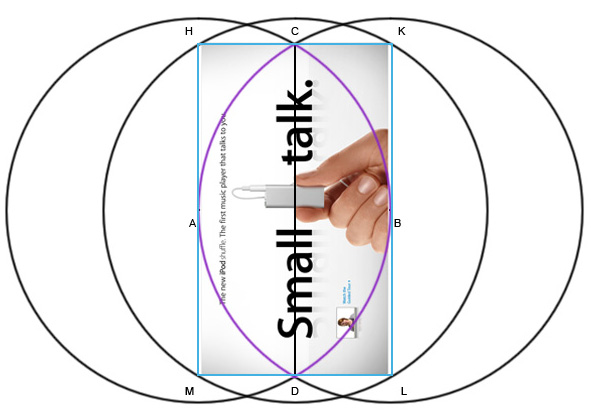
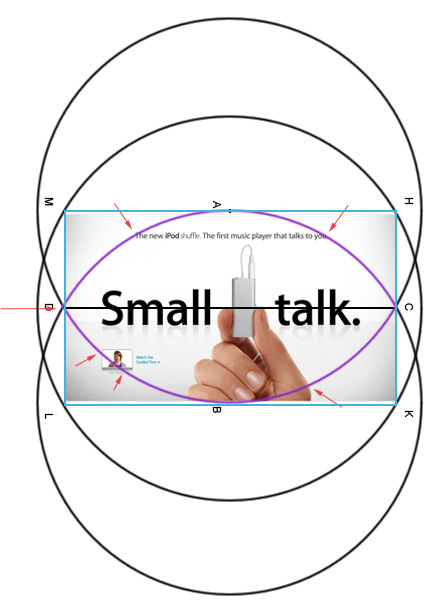
Ага! Вот вы и попались. Давайте ка посмотрим поближе.

Обратите внимание как потрясающе дизайны Apple используют эту разметочную сетку. Этому геометрическому построению я даже не знаю сколько сотен лет. Оно использовалось в иконах, храмах, скульптурах. Современные дизайнеры мастерски используют его в обычных коммерческих вещах и оно продолжает безотказно работать. Их вещи покупают вопреки всякому смыслу.

Что же это мистика? Расчет? Геометрия? Философия? Нам остается только практиковаться и пытаться узнать это самим

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Корень из трех на числовой окружности

Вопрос по алгебре:

Корень из -3 на числовой окружности покажите

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Речь идет о комплексных числах
√-3=√3i=√3(cosП/2+isinП/2)

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Алгебра.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.

Видео:Тригонометрическая окружность. Как выучить?Скачать

Корень из трех на окружности

Видео:Отбор корней по окружностиСкачать

Корень из трех на окружности

Вопрос по алгебре:

Корень из -3 на числовой окружности покажите

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Речь идет о комплексных числах
√-3=√3i=√3(cosП/2+isinП/2)

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Алгебра.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.

Видео:Как искать точки на тригонометрической окружности.Скачать

Философская геометрия, Часть 2. Корень из трех и его практическое применение

Сейчас я вам что покажу, закачаетесь. Обязательно загляните под кат, самые интересные картинки я припрятал там.

Я продолжаю рассказ о применении философской геометрии на практике. Прошлая часть была обзорная, она говорила о том, что многие века геометрия использовалась для поиска универсальных идеальных законов природы. Эти законы повсеместно использовались в произведениях искусства, архитектуре и духовной жизни.

Сегодня я расскажу про замечательную пропорцию «корень из трех». Я покажу ее сакральный смысл, а под катом продемонстрирую пример из современного дизайна, который повергнет вас в шок 😉

Начнем с построения пропорции. Возьмем отрезок AB.

Примем его за радиус и построим окружность с центром в A.

Теперь построим вторую окружность с тем же радиусом, но с центром в B.

У нас получилась фигура ACBD, имеющая огромное значение для наших предков. Она называется Vescica Piscis (пузырь рыбы). Самый простой и важный пример — она давно является символом христианства.

Я продолжу под катом. Спорим, никогда не догадаетесь чем там все закончится 🙂

Ну вот, раз мы уже под катом, начну сыпать картинки. Мы остановились на Vescica Piscis и символе христианства. Вот Христос вписан в эту фигуру.

Вот здесь изображено много символической рыбы.

Кстати, впервые я про это узнал, купив вот такую подвеску в Кафедральном соборе Уппсалы. Так что символ вполне используется и сейчас.

Но чем же так примечательна фигура? Давайте вернемся к построениям. Соединим точки C и D, а из места их пересечения нарисуем еще одну окружность с радиусом AB. Нарисуем прямоугольник HKLM.

Этот прямоугольник обладает замечательным свойством. Его высота относится к ширине ровно как корень их трех (√3 / 1). Корень из трех — это одно из основных иррациональных чисел, но основе которых строилось множество картин, зданий и просто предметов.

Но если вы думаете, что это все старо, уныло и протухло, то вы ошибаетесь. Я обещал сюрприз. Готовы? Только громко не смейтесь.

Да-да, это он. iPhone не идеально помещается в этот прямоугольник, но его размеры чрезвычайно близки. Мне кажется что это не совпадение вот почему.
Корень из трех — это примерно 1.732050…
Отношение сторон айфона первого поколения (115×61) примерно равно 1.88524.
iPhone 3G (115.5×61.8) — 1.8599
iPod Touch (110×61.8) — 1.779

Смотрите, они стремятся к идеалу! Мешать им могут только тысячи технических причин.

Удивлены? Смущены? Не верите? Сейчас будет больше. Зайдем на apple.com

Хм… Что-то мне этот центральный блок напоминает. А ну ка…

Ага! Вот вы и попались. Давайте ка посмотрим поближе.

Обратите внимание как потрясающе дизайны Apple используют эту разметочную сетку. Этому геометрическому построению я даже не знаю сколько сотен лет. Оно использовалось в иконах, храмах, скульптурах. Современные дизайнеры мастерски используют его в обычных коммерческих вещах и оно продолжает безотказно работать. Их вещи покупают вопреки всякому смыслу.

Что же это мистика? Расчет? Геометрия? Философия? Нам остается только практиковаться и пытаться узнать это самим

Видео:Алгебра 10 класс. 20 сентября. Числовая окружность #6 координаты точекСкачать

Тригонометрический круг: вся тригонометрия на одном рисунке

Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.

Вот что мы видим на этом рисунке:

Видео:Задание №13. Как отбирать корни в тригонометрической окружности? 🤔Скачать

А теперь подробно о тригонометрическом круге:

Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.

Мы отсчитываем углы от положительного направления оси против часовой стрелки.

Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.

Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Всё это легко увидеть на нашем рисунке.

Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :

Простым следствием теоремы Пифагора является основное тригонометрическое тождество:

Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).

Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.

Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.

Легко заметить, что

Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:

где — целое число. То же самое можно записать в радианах:

Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,

📸 Видео

3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать

Отбор корней по окружностиСкачать

10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

Корень в столбик sqrt3Скачать

Графические параметры. Интенсив 2024Скачать

Три способа отбора корней в задании 13 ЕГЭ профильСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Корень из двух – первая математическая трагедия // Vital MathСкачать

Как отбирать корни с помощью числовой окружности? Тригонометрические уравнения Часть 6 из 6Скачать

СЛОЖИТЕ ДВА КОРНЯСкачать

Точки на числовой окружностиСкачать

Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

3 СПОСОБА ОТБОРА КОРНЕЙ В ЗАДАНИИ #12 (по окружности, неравенством и подбором)Скачать