Простейшие геометрические фигуры карандашом – начальная стадия рисования любого объекта. Об этом свидетельствует компьютерное моделирование. Как и компьютерные трехмерные объекты включают в себя множество фигур, изображение делится на формы.
Видео:Урок 06. Конус. Как сделать супер ОБЪЕМНЫЙ рисунок на примере конусаСкачать

Особенности построения геометрических фигур
Рисунок геометрических фигур карандашом имеет такие этапы:
| № | Этап | Описание |
| 1 | Анализ модели | Необходимо представить фигуру как каркас из точек и линий. Прорисовывание невидимых линий – главный методологический прием, помогающий рисовать сложные модели. |
| 2 | Наметка линий и вершин | Для этого нужно совершать легкие скользящие движения карандашом, не надавливая на него слишком сильно. |
| 3 | Обозначение видимых ребер | Следует детально прорисовать линии, которые видимы зрителю. Например, если изображается шар или конус, то детально прорисовываются края формы. |
| 4 | Штриховка | С ее помощью можно отобразить расположение теней. |
Штриховка
Штриховка – важный элемент в изображении трехмерных объектов. С ее помощью художник передает тень.
Правила, которые следует запомнить начинающему творцу, следующие:
- Штриховка выполняется только по форме предмета. Иногда можно совмещать штриховки, что способствует усилению тени.
- Заполнение штрихом следует начинать с теневых областей. Если это куб, то штрихами должна быть заполнена 1 из его граней, а границей светотени станут ребра куба. В случае с шаром, цилиндром и конусом границы не четкие, а более размытые.
- Предпочтение лучше отдавать вертикальной штриховке. Начинать следует от ближней части и затем следовать дальше – вглубь рисунка, при этом уменьшая нажим карандашом. От этого штрих светлеет и становится заметно, как поверхность постепенно уходит вдаль.
- Освещенную область нужно начинать штриховать от себя.
Свет и тень
Любая тень образуется, если имеется источник света. Художник должен заранее определить, где именно располагается этот источник и с какой стороны падают на предмет лучи. Если при рисовании возникают трудности со светотенью, следует потренироваться на простом варианте.
Применять можно одну из 2-х техник – штриховку или растушевку. Перед работой рекомендуется включить свет, который будет направлен на предмет. Также важно, чтобы в помещении не было других, более ярких источников света.
Начинающий художник должен запомнить, что существуют следующие участки на рисунке:
| Участок | Описание |
| Блик | Часть рисунка, отражающая свет лампы или солнечного луча. |
| Свет | Области, освещенные лучами под прямым углом. |
| Полутень | Области, располагающиеся между светом и тенью. Их еще называют промежуточными. |
| Тень | Это не освещенные области. |
| Рефлекс | Это освещаемый участок, который получается от предметов поблизости. Огромную роль играет яркость падающего света: чем он ярче, тем более насыщенной будет тень. |
| Падающая тень | Тень от фигуры на то, что находится вокруг. Например, на горизонтальную поверхность, где располагается фигура или стена возле нее. |
Важно уметь находить границу между светом и тенью. Ее форма зависима от рисуемого изображения. К примеру, на шаре эта граница одна, а на кубе – другая. Проблема поиска границы заключена в том, что она обычно размытая. Изредка она бывает четкой: чем ярче свет, тем четче граница.
Например:
- если посмотреть на шар, находящийся под яркими прямыми лучами, можно заметить, что граница светотени имеет изгиб и похожа на овал;
- в случае с цилиндром граница превратится в прямую линию;
- на кубе эта граница проходит прямо по ребру.
В изобразительном искусстве применяется прием, носящий название – «кьяроскуро». Он основан на противопоставлении освещенной и затененной областей. При искусственном освещении образуется среда, где свет становится слишком ярким, а тень – очень темной, что придает насыщенности и резкости.
Видео:подготовка к поступлению в художственное училище. рисуем базу конусСкачать

Рисование в перспективе: куб
Рисунок геометрических фигур карандашом следует начинать с куба.
Обычно применяется белая гипсовая модель, на которой отчетливо видна светотень. Модель лучше приобрести или сделать самостоятельно, фотографию использовать не рекомендуется.
Для изображения необходимо:
- Наметить местоположение фигуры. Разместить ее немного выше центра листа, при этом она должна быть подвинута в сторону теневой области. Это способствует равновесию композиции.
- Провести первую вертикальную линию. Это будет ближайшее к зрителю ребро куба. Засечками нужно ограничить высоту куба.
- Изобразить основание фигуры. Начинать необходимо с видимых линий, точно определив углы их наклона.
- Нарисовать линии, располагающиеся вверху. Перед этим необходимо вспомнить принципы линейной перспективы. Один из них гласит: видимый размер фигур при удалении становится меньше. Линия горизонта располагается на уровне глаз, однако при изменении положения головы эта линия может подняться или опуститься.

- Определить, как сократились боковые грани фигуры.
- Нарисовать дальние линии, не забывая про линии, которые не видны.
- После выполнения и проверки построения выделить ближайшие линии. Чем они ближе, тем более темными их следует сделать.
- Выполнить штриховку. Сначала заполнить штрихом теневые области, а затем перейти к освещенной поверхности. Ближний угол следует оставлять незаштрихованным, а дальнюю часть заполнить легким штрихом.
- Подчеркнуть объем формы, сделав тональные акценты.
Видео:Как начертить КОНУС С ВЫРЕЗОМ (чертеж + аксонометрия)Скачать

Рисование геометрических тел вращения
Геометрические тела вращения начинают рисовать только после освоения изображения куба. Изначально фигуры изображают по отдельности, после – пробуют натюрморт.
Для успеха прорисовывания сложных форм, начинают с изображения простых. Модели можно приобрести в магазине или изготовить своими силами. Для этого используется картон или толстая бумага.
Фигуры нельзя заменять их фотографиями: срисовывание объемных фигур с плоской поверхности лишено смысла и не несет пользы.
Конус
Слово «конус» имеет греческое происхождение. Оно переводится как «сосновая шишка». Такое название фигуре дали потому, что она похожа на шишку или на колпак.
Если же выражаться математическим языком, эта фигура является симметричным телом, которое образуется вследствие объединения лучей, берущих начало из 1-й точки (вершины конуса) и проходящих через плоскую поверхность.
Основанием является круг. Если установить модель конуса основанием на горизонтальную поверхность и посмотреть на нее сбоку, она предстанет перед глазами как треугольник.
Однако в зависимости от угла, под которым смотрят на фигуру, нижняя ее часть, может превращаться в полукруг, поэтому при изображении конуса следует учитывать угол зрения. Также важно, с которой стороны на фигуру падает свет для последующего наложения штриховки.

Рисовать карандашом объемную геометрическую фигуру конуса следует следующим образом:
- Наметить место и размеры фигуры, которая не должна быть очень маленькой или, наоборот, большой. Конус располагается выше середины листа: его верхняя часть оптически более легкая, за счет большего свободного пространства.
- Наметить верхнюю часть фигуры и провести горизонтальную линию. Она будет исполнять роль оси основания.
- Обозначить ширину основания засечками.
- Провести вертикаль по центру фигуры.
- Соединить вершины с основанием.
- Визуально сделать крайние линии удаленными от зрителя, сделав их светлее.
- Строить эллипс: для передачи объема ближняя часть овала должна быть более темной.
- Продолжить работу над объемом. Для этого найти границу тени и света в вершине фигуры и проходящую к основанию. Верхняя часть линии должна быть четкой, а ее отдаленный край – более светлым.
- Осуществить штриховку, двигаясь по вертикали от вершины и доводя до основания. Чтобы лучше передать форму, ввести штрихование и по горизонтали.
- Обозначить контраст света и тени, сделав верхнюю часть более светлой. От горизонтальной поверхности, на которой установлена фигура, подсветить теневую часть.
Цилиндр
Цилиндр имеет 2 основания – внизу и вверху. Оба они имеют форму круга и абсолютно равны по размеру. Образующая цилиндра – вертикаль, расположенная перпендикулярно основанию.

Рисунок геометрических фигур карандашом в форме цилиндра выполняется в следующем порядке:
- На листе обозначить местоположение объекта и легкой штриховкой выявить объем формы. Не нужно слишком надавливать на карандаш, особенно когда рисуются вспомогательные линии. Применение ластика лучше сводить к минимуму.
- Определить высоту и ширину фигуры.
- Провести ось. Она должна делить фигуру пополам.
- Проконтролировать, чтобы верхний эллипс был чуть меньше. При взгляде на модель легко заметить, что верхнее основание развернуто меньше.
- Перейти к работе со светотенью. Граница ее прорисовывается по вертикали от одного основания к другому. Учитывая плавность изменения формы, сделать границу размытой. Штрих следует вертикально. Области, которые удаляются, на свету темнеют, а в тени становятся светлыми. Верхний эллипс попадает в область полутени, если источник света находится сбоку.
- Уточнить форму. Для этого используется штриховка в горизонтальном направлении. Поскольку верхняя часть приближена к свету, она должна быть немного светлее.
Шар считается простейшей фигурой, недаром такую форму под воздействием сил природы приобретают все планеты и звезды. Однако изобразить шар – задача не из простых.
Первые трудности могут возникнуть с рисованием окружности, затем приходится сталкиваться с серьезными проблемами, появляющимися при штриховке.
Перед работой модель шара рекомендуется осветить мягким светом. В этом случае не будет резких теней, что значительно упростит задачу.
Последовательность рисования шара следующая:
- Изобразить окружность, которая станет основой фигуры. В центре бумаги провести прямую, а в центре этой прямой поставить точку. Через нее провести еще 1 прямую, перпендикулярную 1-й. При проведении этих линий не нужно сильно давить на карандаш.
Крайние точки линий нужно соединить так, чтобы образовалась окружность. - Наложить тени. Нужно определить, откуда попадает свет, и поставить точку в самой освещенной части. Ширину тени необходимо отметить штриховкой.
- Провести диаметр через центр фигуры перпендикулярно лучам света.
- На основании диаметра изобразить эллипс. Он обозначает границы светотени.
- Поверхность фигуры условно разделить на несколько областей в зависимости от степени освещенности. Самая светлая область – это блик, ее можно оставить не закрашенной. Вокруг нее – светлое пятно, а далее постепенно переходить к тени. Изображать тень нужно дугообразными штрихами.




Для рисования натюрмортов из геометрических фигур необходимо:
- Подготовить 3-4 фигуры с разными характеристиками. Например, это может быть куб, шар и цилиндр.
- Расставить фигуры и подготовить драпировку ткани, на которой они стоят.
- Выставить спокойное, рассеянное освещение.
- Выбрать ракурс для срисовывания. Лучше, если он будет фронтальным.
- Определиться с расположением рисунка и приступить к работе.
Для начинающего художника рисование геометрических фигур карандашом подобно обучению алфавита для тех, кто изучает язык. Такая тренировка поможет в дальнейшем при создании сложных фигур и композиций на бумаге.
Видео:«КАК РИСОВАТЬ ШЕСТИГРАННУЮ ПИРАМИДУ?» Цикл уроков от Дениса Чернова | Урок №2 | AkademikaСкачать

Видео о рисовании геометрических фигур
Рисунок геометрических фигур карандашом:
Видео:Построение конусаСкачать

Конус и треугольник рисунок
Так как все образующие конуса равны, то его осевым сечением является равнобедренный треугольник, боковыми сторонами которого являются образующие конуса, а основанием — диаметр конуса. При этом все осевые сечения конуса — равные равнобедренные треугольники . На рисунке 168 осевым сечением конуса является треугольник ABP ( АР = ВР ). Угол АPВ называют углом при вершине осевого сечения конуса .
Конус, в осевом сечении которого правильный треугольник, называется равносторонним конусом.
Если секущая плоскость проходит через вершину конуса, пересекает конус, но не проходит через его ось, то в сечении конуса также получается равнобедренный треугольник (см. рис. 168: △ DCP ).
Так как конус — тело вращения, то любое сечение конуса плоскостью, перпендикулярной его оси (т. е. параллельной основанию конуса), есть круг, а сечение боковой поверхности конуса такой плоскостью — окружность этого круга; центром круга (окружности) является точка пересечения оси конуса и секущей плоскости (рис. 169).
Если секущая плоскость не параллельна плоскости основания конуса и не пересекает основание, то сечением боковой поверхности конуса такой плоскостью является эллипс (рис. 170). Поэтому эллипс называют коническим сечением .

О конических сечениях можно прочитать в очерках «Элементарная геометрия», «Проективная геометрия» в конце этой книги.
ЗАДАЧА (3.047). Высота конуса равна радиусу R его основания. Через вершину конуса проведена плоскость, отсекающая от окружности основания дугу: а) в 60 ° ; б) в 90 ° . Найти площадь сечения.
Решени е. Рассмотрим случай а). Пусть плоскость α пересекает поверхность конуса с вершиной Р по образующим РА и РВ (рис. 172); △ АВР — искомое сечение. Найдём площадь этого сечения.
Хорда АВ окружности основания стягивает дугу в 60 ° , значит, △ AOB — правильный и АВ = R .
Если точка С — середина стороны АB, то отрезок PC — высота треугольника АВР. Поэтому S △ ABP = 



Тогда S △ ABP = 

Ответ: а) 
18.3. Касательная плоскость к конусу
Определение. Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса перпендикулярно осевому сечению, проведённому через эту образующую.
Говорят, что плоскость α касается конуса по образующей РА (рис. 173): каждая точка образующей РА является точкой касания плоскости α и данного конуса.
Через любую точку боковой поверхности конуса проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности конуса можно провести лишь одну плоскость, касательную к данному конусу в этой точке.
18.4. Изображение конуса
Для изображения конуса достаточно построить: 1) эллипс, изображающий окружность основания конуса (рис. 174); 2) центр О этого эллипса; 3) отрезок ОР, изображающий высоту конуса; 4) касательные прямые РА и PB из точки Р к эллипсу (их проводят с помощью линейки на глаз).
Для достижения наглядности изображения невидимые линии изображают штрихами.
Необходимо заметить, что отрезок АВ, соединяющий точки касания образующих и окружности основания конуса, ни в коем случае не является диаметром основания конуса, т. е. этот отрезок не содержит центра О эллипса. Следовательно, △ АBP — не осевое сечение конуса. Осевым сечением конуса является △ ACP, где отрезок AC проходит через точку О, но образующая PC не является касательной к окружности основания.
18.5. Развёртка и площадь поверхности конуса
Пусть l — длина образующей, R — радиус основания конуса с вершиной Р .
Поверхность конуса состоит из боковой поверхности конуса и его основания. Если эту поверхность разрезать по одной из образующих, например по образующей PA (рис. 175), и по окружности основания, затем боковую поверхность конуса развернуть на плоскости (рис. 176, a ), то получим развёртку поверхности конуса (рис. 176, б ), состоящую из: а) кругового сектора, радиус которого равен образующей l конуса, а длина дуги сектора равна длине окружности основания конуса; б) круга, радиус которого равен радиусу R основания конуса. Угол сектора развёртки боковой поверхности конуса называют углом развёртки конуса ; его численная величина равна отношению длины окружности основания конуса к его образующей (радиусу сектора развёртки):
α = 
За площадь боковой поверхности конуса принимается площадь её развёртки. Выразим площадь боковой поверхности конуса через длину l его образующей и радиус R основания.
Площадь боковой поверхности — площадь кругового сектора радиуса длины l — вычисляется по формуле
S бок = 
где α — величина угла (в радианах) сектора — развёртки. Учитывая, что α = 
Таким образом, доказана следующая теорема.
Теорема 27. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. ▼
Площадь полной поверхности конуса равна сумме площадей его боковой поверхности и основания, т. е.
S кон = π Rl + π R 2 . (3)
Следствие. Пусть конус образован вращением пря м оугольного треугольника ABC вокруг катета АС (рис. 177). Тогда S бок = π • BC • АВ. Если D — середина отрезка АВ, то AB = 2 AD, поэтому
S бок = 2 π ВС • AD. (4)
Проведём DE ⟂ АB ( E ∈ l = AС ) . Из подобия прямоугольных треугольников ADE и ACB (у них общий угол А ) имеем


Тогда соотношение (4) принимает вид
S бок = (2 π • DE ) • AC, (6)
т. е. площадь боковой поверхности конуса равна произведению высоты конуса на длину окружности, радиус которой равен длине серединного перпендикуляра, проведённого из точки на оси конуса к его образующей.
Это следствие будет использовано в п. 19.7.
18.6. Свойства параллельных сечений конуса

Теоремa 28. Если конус пересечён плоскостью, параллельной основанию, то: 1) все образующие и высота конуса делятся этой плоскостью на пропорциональные части; 2) в сечении получается круг; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.
Доказательств о. 1) Пусть конус с вершиной Р и основанием F пересечён плоскостью α , параллельной плоскости β основания конуса и расположенной между Р и β (рис. 178).
Проведём высоту РО конуса, где точка О — центр круга F. Так как РО ⟂ β , α || β , то α ⟂ РО. Значит, в сечении конуса плоскостью α получается круг с центром в точке O 1 = α ∩ РО. Обозначим этот круг F 1 .
Рассмотрим гомотетию 
Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия 



где k — коэффициент гомотетии 
А поскольку гомотетия является подобием, то круг F 1 , являющийся параллельным сечением конуса, подобен его основанию.
Вследствие того что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии и k = PO 1 : Р О , где РO 1 и PO — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то
S сечен : S основ = k 2 = 
18.7. Вписанные в конус и описанные около конуса пирамиды
Определение. Пирамида называется вписанной в конус, если у них вершина общая, а основание пирамиды вписано в основание конуса. В этом случае конус называется описанным около пирамиды.
Для построения изображения правильной пирамиды, вписанной в конус:
— строят изображение основания пирамиды — правильного многоугольника, вписанного в основание конуса;
— соединяют отрезками прямых вершину конуса с вершинами построенного многоугольника;
— выделяют видимые и невидимые (штрихами) линии изображаемых фигур.
На рисунках 179—182 изображена вписанная в конус пирамида, в основаниях которой лежит:
— прямоугольный треугольник (см. рис. 179);
Видео:Как научиться рисовать конус. Объяснение за 5 минут. УРОК 7Скачать

Что такое конус: определение, элементы, виды
В данной публикации мы рассмотрим определение, основные элементы и виды одной из самых распространенных фигур в пространстве – конуса. Представленная информация сопровождается соответствующими рисунками для лучшего восприятия.
Видео:Натюрморт из геометрических предметовСкачать

Определение конуса
Далее мы будем рассматривать самый распространенный вид конуса – прямой круговой. Остальные возможные варианты фигуры перечислены в последнем разделе публикации.
Итак, прямой круговой конус – это трехмерная геометрическая фигура, полученная путем вращения прямоугольного треугольника вокруг одного из своих катетов, который в данном случае будет являться осью фигуры. Ввиду этого иногда такой конус называют конусом вращения.
Конус на рисунке выше получен в результате вращения прямоугольного треугольника ACD (или BCD) вокруг катета CD.
Видео:Как начертить конус в объемеСкачать
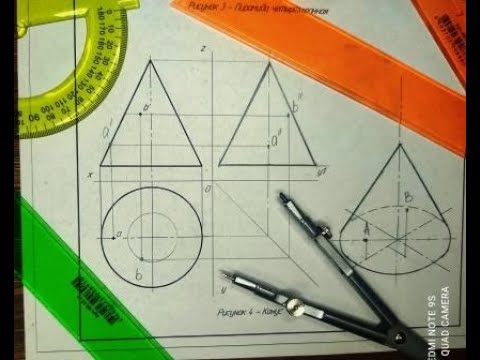
Основные элементы конуса
- R – радиус круга, являющегося основанием конуса. Центр круга – точка D, диаметр – отрезок AB.
- h (CD) – высота конуса, одновременно являющаяся осью фигуры и катетом прямоугольных треугольников ACD или BCD.
- Точка C – вершина конуса.
- l (CA, CB, CL и CM) – образующие конуса; это отрезки, соединяющие вершину конуса с точками на окружности его основания.
Между образующей конуса, его высотой и радиусом основания есть взаимосвязь (согласно теореме Пифагора):
Развёртка конуса – боковая поверхность конуса, развернутая в плоскость; является круговым сектором.
- длина дуги сектора равняется длине окружности основания конуса (т.е. 2πR );
- α – угол развёртки (или центральный угол);
- l – радиус сектора.
Примечание: Основные свойства конуса мы рассмотрели в отдельной публикации.
🎦 Видео
Урок ИЗО в школе. 6 класс. Урок № 11. «Натюрморт из геометрических тел».Скачать

Конус. 11 класс.Скачать

ТЕМА 5. ПОСТРОЕНИЕ ШЕСТИГРАННОЙ ПРИЗМЫ, КОНУСА И ЧЕТЫРЕХГРАННОЙ ПИРАМИДЫ.Скачать

Геометрия 11 класс (Урок№7 - Конус.)Скачать

Урок №7. Рисунок | Рисунок 3-х геометрических тел, контрастных по форме и тону на светлом фонеСкачать

Построение линии пересечения поверхности конуса с проецирующей плоскостьюСкачать

Конус с вырезомСкачать
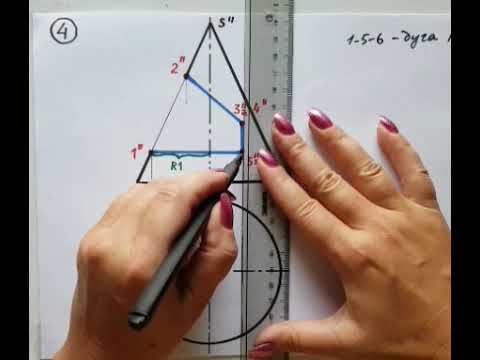
УРОК 3.КАК НАРИСОВАТЬ ПРИЗМУ,ПИРАМИДУ.Обучение рисунку.Урок рисования карандашом.построение поэтапноСкачать

Академический рисунок кубаСкачать

Здравствуйте. Тема «Геометрические фигуры» от 22.12.20 натюрморт, карандашСкачать

Как научиться ложить штрих по форме предмета? Рисуем основные фигуры. Шаг за шагом.Скачать

ТЕМА 2. ПОСТРОЕНИЕ КУБА, ЦИЛИНДРА, ШАРАСкачать


















