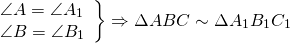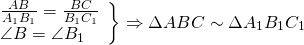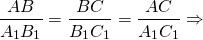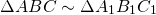Когда три треугольника подобны (2 видео)

Подобные треугольники

Содержание

Определение
Признаки подобия треугольников
Свойства подобных треугольников
Примеры наиболее часто встречающихся подобных треугольников
Признаки подобия треугольников
Подобные треугольники
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
💥 Видео

Видео:№561. Докажите, что два равносторонних треугольника подобны.Скачать

Определение

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.

Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.

Видео:№560. Подобны ли треугольники ABC и A1B1C1, если: а) АВ = 3 см, ВС=5 см, СА=7 см, А1В1=4,5см,Скачать

Признаки подобия треугольников

I признак подобия треугольников

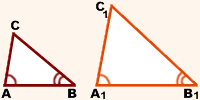
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II признак подобия треугольников

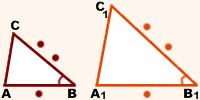
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Свойства подобных треугольников

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Отношение периметров подобных треугольников равно коэффициенту подобия.
Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.

Видео:8 класс, 22 урок, Первый признак подобия треугольниковСкачать

Примеры наиболее часто встречающихся подобных треугольников

1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.

2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –

3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

Здесь вы найдете подборку задач по теме «Подобные треугольники» .

Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Признаки подобия треугольников

Признаки подобия треугольников позволяют доказать, что треугольники являются подобными, на основании 2-3 равенств (вместо 6 по определению).

В школьном курсе геометрии, как правило, изучают три признака подобия произвольных треугольников.

( подобие треугольников по двум углам)

Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

( подобие треугольников по двум сторонам и углу между ними)

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.

( подобие треугольников по трём сторонам)

Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.

Есть еще 4-й признак подобия треугольников —

( подобие треугольников по двум сторонам и наибольшему углу)

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а наибольший угол одного равен наибольшему углу другого, то такие треугольники подобны.

Доказав, что треугольники подобны, можно использовать свойства подобных треугольников.

Для доказательства подобия прямоугольных треугольников используют другие признаки. Их мы запишем в следующий раз.

Подобие правильных и подобие равнобедренных треугольников рассмотрим позже.

Признаки подобия треугольников широко используются при решении задач как в курсе планиметрии, так и в курсе стереометрии. Например, на основании подобия прямоугольных треугольников доказывается свойство биссектрисы треугольника.

Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Подобные треугольники

Подобные треугольники — это треугольники, у которых все три угла равны, а все стороны одного треугольника в одно и то же число раз длиннее (или короче) сторон другого треугольника, то есть треугольники подобны если их углы равны, а сходственные стороны пропорциональны.

Сходственные стороны — это стороны двух треугольников, лежащие против равных углов.

Рассмотрим два треугольника ABC и A₁B₁C₁, у которых ∠A = ∠A₁, ∠B = ∠B₁, ∠C = ∠C₁:

Стороны AB и A₁B₁, BC и B₁C₁, CA и C₁A₁, лежащие напротив равных углов, называются сходственными сторонами. Следовательно, отношения сходственных сторон равны:

AB	=	BC	=	AC	= k,
A₁B₁		B₁C₁		A₁C₁

k — это коэффициент подобия ( число, равное отношению сходственных сторон подобных треугольников). Если k = 1, то треугольники равны, то есть равенство треугольников – это частный случай подобия.

Подобие треугольников обозначается знаком

: ABC

A₁B₁C₁.

Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Если обозначить площади двух подобных треугольников буквами S и S₁, то:

S	= k 2 .
S₁

Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Первый признак подобия треугольников

Если два угла одного треугольника равны двум углам другого, то треугольники подобны.

то ABC

A₁B₁C₁.

Видео:Геометрия Подобны ли два треугольника, если стороны одного относятся как 3:8:9, а стороны другогоСкачать

Второй признак подобия треугольников

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то треугольники подобны.