Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
КАРТА – СХЕМА УЧЕБНОГО ЗАНЯТИЯ
продолжительность — 90 минут
Тема занятия: Декартово произведение и разбиение множеств на классы
расширить знания студентов с темы действия с множествами, рассмотреть Декартово произведение, разбиение множеств на классы;
способствовать развитию памяти, внимания, логического мышления;
создать условия для применения полученных знаний при выполнении расчетных заданий.
Необходимое аппаратное и программное обеспечение:
Карточки с заданиями самостоятельной работы
Стойлова АП. Математика : учебник для студ. учреждений высш.образования / Л.П. Стойлова. — 4-е изд., стер. — М. : Издательский центр «Академия», 2014.
Стойлова АП. Математика : учебник для студ. учреждений высш.образования / Л.П. Стойлова. — 4-е изд., стер. — М. : Издательский центр «Академия», 2014.
Тип и вид учебного занятия:
ОРГАНИЗАЦИОННАЯ СТРУКТУРА УРОКА
Содержание и виды деятельности преподавателя
1. Организационный этап
Приветствие, выявление отсутствующих, информирование о теме и целях занятия.
2. Актуализация ЗУН
— Что такое множество? Что означает задать множество?
— Способы задания множеств
— Что такое подмножество?
-какие действия выполняем над множествами?
— Что такое пересечение? Объединение?
— Какие свойства пересечения, объединения?
Самостоятельная работа (с взаимопроверкой)
Найдите: а) А∩В; б) А∩С; в) С∩В.
Найдите: а) АUВ; б) АUС; в) СUВ.
Найдите а)(А∩В)∩С; б) )(А


3. Изучение нового материала
— разбиение множеств на классы
4. Первичное закрепление
Практическое выполнение заданий
5. Информация о домашнем задании
Методические рекомендации для самостоятельной работы
6. Подведение итогов урока
Подведение итогов работы группы, отдельных студентов.
Корректирование пробелов знаний.
В начальных классах ученики решают задачу: используя цифры 1, 2, 3 образовать всевозможные двузначные числа.
Путем перебора дети получают:
Запись каждого числа состоит из двух цифр, причем существенен порядок их следования. Например, из цифр 1, 2 образованы числа 12 и 21.
В том случае, когда важен порядок следования элементов множества, в математике говорят об упорядоченных наборах элементов. В данной задаче – упорядоченные пары (а; b), образованные из элементов а и b. Это (1; 2), (1; 3), (1; 4) и т.д. Первый элемент а называют первой координатой пары, элемент b – второй.
Значит, в нашей задаче мы оперировали множеством А=<1, 2, 3> и образовывали всевозможные пары.
Рассмотрим другой пример. Пусть А=, B=. Образуем всевозможные пары (а;b) так, что а

Декартовым произведением множеств А и В называется множество пар, первая компонента которых принадлежит множеству А, вторая множеству В. Обозначают А



Операцию нахождения декартового произведения множеств А и В называют декартовым умножением этих множеств.
Рассмотрим следующий пример. Известно, что А
Перечислим элементы, принадлежащие множеству А
А= <a, b, c,d>, B=A. Декартово произведение А
(a, d), (b, a), (b, b), (b, c), (b, d), (c, a), (c, b), (c, c), (c, d), (d, a), (d, b) ,(d, c), (d, d)>.
Количество пар в декартовом прoизведении А


В математике рассматривают не только упорядоченные пары, но и наборы из трех, четырех и т.д. элементов. Такие упорядоченные наборы называют кортежами. Так, набор (1, 5, 6) есть кортеж длины 3, так как в нем три элемента.
Используя понятие кортежа, можно определить понятие декартового произведения n множеств.
Декартовым произведением множеств А








Пусть даны множества А





(2, 5, 8),(3, 3, 7), (3, 4, 7), (3, 3, 8), (3, 4, 8), (3, 5, 7), (3, 5, 8)>.
Понятие разбиения множества на классы
Понятие множества и операций над множествами позволяют уточнить представление о классификации.
Классификация – это действие распределения объектов по классам на основании сходств внутри класса и их отличия от других объектов. Классификация широко применяется в математике.
Например, натуральные числа делятся на четные и нечетные; углы бывают острые, тупые и прямые и т.д.
Любая классификация связана с разбиением некоторого множества объектов на подмножества.
Считают, что множество Х разбито на классы Х


1) подмножества Х


2) объединение этих подмножеств совпадает с множеством Х.
Если не выполнено хотя бы одно из этих условий, классификацию считают неправильной.
Например: а) Множество треугольников Х разбито на три класса: остроугольные, прямоугольные и тупоугольные. Действительно, выделенные подмножества попарно не пересекаются, а их объединение совпадает с множеством Х; b) Из множества треугольников Х выделили подмножества равнобедренных, равносторонних и разносторонних треугольников. Так как множества равнобедренных и равносторонних треугольников пересекаются, значит, не выполнено первое условие классификации, и разбиения множества Х на классы мы не получили.
Так как разбиение множества на классы связано с выделением его подмножеств, то классификацию можно выполнять при помощи свойств элементов множеств.
Рассмотрим, например, множество натуральных чисел. Его элементы обладают различными свойствами. Нас интересуют числа со свойством «быть кратным 3». Это свойство позволяет выделить из множества N подмножество, состоящее из чисел, кратных 3. Тогда про остальные натуральные числа можно сказать, что они не кратны 3, т.е. получаем еще одно подмножество множества N. Так как выделенные подмножества не пересекаются, а их объединение совпадает с множеством N, то имеем разбиение данного множества на два класса.
Вообще, если на множестве Х задано одно свойство, то это множество разбивается на два класса. Первый – это класс объектов, обладающих данным свойством, а второй – дополнение первого класса до множества Х. Во втором классе содержатся такие объекты множества Х, которые заданным свойством не обладают. Такую классификацию называют дихотомической.
Рассмотрим ситуацию, когда для элементов множества заданы два свойства. Например, свойства натуральных чисел: «быть кратным 3» и «быть кратным 5». При помощи этих свойств из множества N можно выделить два подмножества: А – множество чисел, кратных 3 и В – множество чисел, кратных 5. Эти множества пересекаются, но ни одно из них не является подмножеством другого (рис. 13). Разбиения на подмножества А и В в данном случае на произошло. Но круг, изображающий множество N, можно рассматривать как состоящий из четырех непересекающихся областей. Каждая область изображает некоторое подмножество множество N. Множество I состоит из чисел, кратных 3 и 5, множество I – из чисел, кратных 3 и не кратных 5, множество III – из чисел, кратных 5 и не кратных 3, множество IV – из чисел, не кратных 3 и не кратных 5. Объединение этих четырех множеств есть множество N.
Таким образом, выделение двух свойств привело к разбиению множества N натуральных чисел на четыре класса.
Не следует думать, что задание двух свойств элементов множества всегда приводит к разбиению этого множества на четыре класса. Например, при помощи таких двух свойств «быть кратным 3» и «быть кратным 6» множество натуральных чисел разбивается на три класса (рис. 14): I – класс чисел, кратных 6; II – класс чисел, кратных 3, но не кратных 6; III – класс чисел, не кратных 3.
Примеры
Приведем несколько примеров разбиения:
1. Множество четырехугольников 
трапеции и прямоугольники. Данные подмножества попарно не пересекаются, а их объединения совпадают с множеством 
2. Множество четырехугольников 
квадраты, параллелограммы, прямоугольники. Так как прямоугольник и квадрат – частные случаи параллелограмма, то данные подмножества пересекаются, значит, не выполнено первое условие классификации, и разбиение множества 
3. Дано множество прямых 

4. Дано множество 




5. Множество 












Решение. Элементами множества А1´ А2 ´А3 будут кортежи длины 3 такие, что первая их компонента принадлежит множеству А1, вторая – множеству А2, третья – множеству А3.
Пример 2. Пусть на множестве Х= задано отношение «меньше» (т.е. первый элемент меньше второго, второй меньше третьего). Записать декартово произведение XX. Из этого множества следует выбрать элементы, которые должны удовлетворять отношению «меньше».
Декартово произведение X Х может быть записано в виде множества из упорядоченных пар:
Из этого множества выбираются элементы, которые удовлетворяют отношению «меньше». В результате получится новое множество из упорядоченных пар:
В новом множестве все пары являются элементами декартова произведения XX. Отношение «меньше» на множестве Х является подмножеством декартова произведения XX. Бинарное отношение на множестве Х есть подмножество декартова произведения W XX.
2) Декартово произведение двух множеств X Y .
Пусть заданы два множества: X = , Y = .
Записать декартово произведение X Y .
Декартово произведение двух множеств равно:
Аналогично можно найти декартово произведение трёх множеств: X Y Z .
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Видео:95 Разбиение множества на классы эквивалентностиСкачать

Понятие разбиения множества на классы
Понятие множества и операций над множествами позволяют уточнить представление о классификации.
Классификация – это действие распределения объектов по классам на основании сходств внутри класса и их отличия от других объектов. Классификация широко применяется в математике.
Например, натуральные числа делятся на четные и нечетные; углы бывают острые, тупые и прямые и т.д.
Любая классификация связана с разбиением некоторого множества объектов на подмножества.
Считают, что множество Х разбито на классы Х


1) подмножества Х


2) объединение этих подмножеств совпадает с множеством Х.
Если не выполнено хотя бы одно из этих условий, классификацию считают неправильной.
Например: а) Множество треугольников Х разбито на три класса: остроугольные, прямоугольные и тупоугольные. Действительно, выделенные подмножества попарно не пересекаются, а их объединение совпадает с множеством Х; b) Из множества треугольников Х выделили подмножества равнобедренных, равносторонних и разносторонних треугольников. Так как множества равнобедренных и равносторонних треугольников пересекаются, значит, не выполнено первое условие классификации, и разбиения множества Х на классы мы не получили.
Так как разбиение множества на классы связано с выделением его подмножеств, то классификацию можно выполнять при помощи свойств элементов множеств.
Рассмотрим, например, множество натуральных чисел. Его элементы обладают различными свойствами. Нас интересуют числа со свойством «быть кратным 3». Это свойство позволяет выделить из множества N подмножество, состоящее из чисел, кратных 3. Тогда про остальные натуральные числа можно сказать, что они не кратны 3, т.е. получаем еще одно подмножество множества N. Так как выделенные подмножества не пересекаются, а их объединение совпадает с множеством N, то имеем разбиение данного множества на два класса.
Вообще, если на множестве Х задано одно свойство, то это множество разбивается на два класса. Первый – это класс объектов, обладающих данным свойством, а второй – дополнение первого класса до множества Х. Во втором классе содержатся такие объекты множества Х, которые заданным свойством не обладают. Такую классификацию называют дихотомической.
Рассмотрим ситуацию, когда для элементов множества заданы два свойства. Например, свойства натуральных чисел: «быть кратным 3» и «быть кратным 5». При помощи этих свойств из множества N можно выделить два подмножества: А – множество чисел, кратных 3 и В – множество чисел, кратных 5. Эти множества пересекаются, но ни одно из них не является подмножеством другого (рис. 13). Разбиения на подмножества А и В в данном случае на произошло. Но круг, изображающий множество N, можно рассматривать как состоящий из четырех непересекающихся областей. Каждая область изображает некоторое подмножество множество N. Множество I состоит из чисел, кратных 3 и 5, множество I – из чисел, кратных 3 и не кратных 5, множество III – из чисел, кратных 5 и не кратных 3, множество IV – из чисел, не кратных 3 и не кратных 5. Объединение этих четырех множеств есть множество N.

Не следует думать, что задание двух свойств элементов множества всегда приводит к разбиению этого множества на четыре класса. Например, при помощи таких двух свойств «быть кратным 3» и «быть кратным 6» множество натуральных чисел разбивается
на три класса (рис. 14): I – класс чисел, кратных 6; II – класс чисел, кратных 3, но не кратных 6; III – класс чисел, не кратных 3.
Видео:Разбиение множества на классыСкачать

Понятие разбиения множества на классы
Дата добавления: 2014-09-06 ; просмотров: 8134 ; Нарушение авторских прав
Понятие множества и операций над множествами позволяют уточнить наше представление о классификации.
Любая классификация связана с разбиением некоторого множества объектов на подмножества.
3) объединение подмножеств совпадает с множеством А.
Если не выполнено хотя бы одно свойство, то классификацию считают неправильной.
Например, если множество треугольников разбить на остроугольные, прямоугольные и тупоугольные, то разбиение будет выполнено верно, т.к. выполнены все условия, данные в определении.
Если из множества треугольников выделить подмножества равносторонних, равнобедренных и разносторонних треугольников, то разбиения мы не получим, т.к. множество равносторонних треугольников является подмножеством равнобедренных треугольников, т.е. не выполняется второе условие разбиения множества на классы.
Пример 1. Пусть А – множество двузначных чисел. Рассмотрим на этом множестве свойство «быть четным».
|
|
Множество А разбилось на два подмножества:
А1 – множество четных чисел,
А2 – множество нечетных чисел, при этом
Т.о. задание одного свойства приводит к разбиению этого множества на 2 класса.
Пример 2. Пусть А – множество треугольников. Рассмотрим на данном множестве два свойства: «быть прямоугольным» и «быть равнобедренным». При помощи этих свойств из множества треугольников можно выделить 2 подмножества: В – множество прямоугольных треугольников и С – множество равнобедренных треугольников. Эти множества пересекаются, но ни одно из них не является подмножеством другого.
По рисунку видно, что получилось 4 класса:
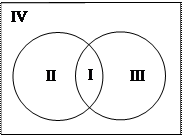
II – В Ç 
III – 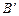
IV – 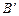
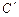
Т.о. с помощью двух свойств множество разбилось на 4 класса, таких, что их пересечение пусто, а их объединение составляет множество А.
Следует отметить, что задание двух свойств приводит к разбиению множества на 4 класса не всегда.
Пример 3. Пусть А – множество треугольников. Рассмотрим на данном множестве два свойства: «быть прямоугольным» и «быть остроугольным». При помощи этих свойств из множества треугольников можно выделить 2 подмножества: В – множество прямоугольных треугольников и С – множество остроугольных треугольников. Эти множества не пересекаются. По рисунку видно, что при помощи этих свойств множество треугольников разбивается на три класса:
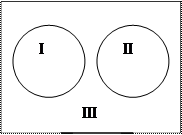
II – множество остроугольных треугольников;
III – множество не прямоугольных, не остроугольных треугольников.
Контрольные вопросы
1. При каких условиях считают, что множество разбито на классы?
2. Как определить число элементов в объединении двух или трех конечных множеств?
📹 Видео
Отношение эквивалентности как разбиение множестваСкачать

Разбиение множества на классы эквивалентности.Скачать

9 класс, 2 урок, Множества и операции над нимиСкачать

Множество. Элементы множества. 5 класс.Скачать

3.3 Отношение эквивалентности | Роман Попков | ИТМОСкачать

РазбиенияСкачать

Что такое классы эквивалентностиСкачать

Отношение эквивалентности, отношение порядкаСкачать

Разбиение множества на классы Подготовка к контрольной работеСкачать

Пересечение множеств. Объединение множеств. 5 класс.Скачать

Алгоритмы. Разбиение множества. Теория.Скачать

Отношения эквивалентностиСкачать

Отношение эквивалентности. Фактор-множество. Отношение порядка. 2020 г.Скачать

Разбиение множеств на равные части.Скачать

Операции над множествамиСкачать

Математика. 3 класс. Множества. ПодмножестваСкачать

Площади треугольников разбиенияСкачать

Урок 48. Множество Элементы множества Пустое множество (6 класс)Скачать

