Кинематическое движение точки по окружности

Положение частицы, движущейся по окружности, можно задать углом 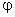, который образует радиус-вектор с каким-либо неизменным направлением, например, осью X.

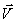
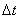
Введем для движения частицы по окружности по аналогии с линейной скоростью угловую скорость и ускорение. Угловая скорость характеризует быстроту изменения угла поворота радиус-вектора, поэтому угловой скоростью называется производная угла поворота радиус-вектора, определяющего положение материальной точки, по времени.Пусть за время точка М повернулась на угол (рис. 1.18), тогда угловая скорость

.

Направление вектора угловой скорости определяется по правилу правого винта. Если рукоятку винта поворачивать по направлению движения точки, то его поступательное движение покажет направление вектора угловой скорости.

При вращении частицы с постоянной по модулю скоростью угловую скорость называют также угловой частотой вращения. Она показывает, на какой угол поворачивается радиус-вектор, определяющий положение материальной точки, за единицу времени. Величина 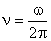дает число оборотов в единицу времени и называется частотой. Время, за которое частица совершает полный оборот, называется периодом вращения .

Вектор угловой скорости может изменяться как за счет изменения скорости вращения тела, так и за счет поворота оси вращения в пространстве. Изменение вектора угловой скорости со временем характеризуется угловым ускорением. Пусть за время вектор получает приращение . Тогда угловое ускорение определится как

.

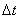
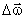
Вектор углового ускорения частицы при неизменной ориентации оси вращения параллелен этой оси и направлен вдоль вектора или против него в зависимости от того, увеличивается или уменьшается угловая скорость.

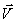
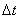
Отдельные точки вращающегося тела имеют различные линейные скорости , при этом скорость каждой из точек непрерывно изменяет свое направление. Можно показать, что модуль линейной скорости точки зависит от угловой скорости и от расстояния от этой точки до оси вращения. Пусть за малый промежуток времени тело повернулось на угол . Точка, находящаяся на расстоянии от оси вращения, проходит при этом путь . Модуль линейной скорости точки равен

.

Таким образом, модули линейной и угловой скорости связаны соотношением

.

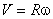
2. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
И ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА

«Ньютон был первым, кто попытался сформулировать элементарные законы, которые определяют временной ход широкого класса процессов в природе с высокой степенью полноты и точности, и оказал своими трудами глубокое и сильное влияние на всё мировоззрение в целом. Самой судьбой Ньютон был поставлен на поворотном пункте умственного развития человечества». А. Эйнштейн

Исаак Ньютон (Isaak Newton), 1643–1727

Выдающийся английский учёный, заложивший основы современного естествознания, создатель классической физики, член Лондонского королевского общества и его президент с 1703г. Работы Ньютона относятся к механике, оптике, астрономии, математике. В двадцать с небольшим лет Ньютон сумел заложить фундамент почти для всего существенного, что кем когда-либо было сделано.

Ньютону было свойственно исключительное трудолюбие. Отрешившись от всего, что происходит вокруг, порой без сна и отдыха, он трудился с невероятной интенсивностью. Ему понадобилось всего 18 месяцев, чтобы завершить большую часть одной из самых выдающихся книг в истории науки «Математические начала натуральной философии», которую теперь обычно называют просто «Начала». Это сочинение было написано в 1687 г. Именно в «Началах» Ньютон сформулировал закон всемирного тяготения, заложил основы классической механики и сформулировал её основные законы. Он одним из первых построил теорию движения небесных тел, создав, таким образом, основы небесной механики. Много лет спустя А. Эйнштейн, обращаясь к Ньютону, писал: «Прости меня, Ньютон: ты нашёл единственный путь, возможный в твоё время для человека величайшей научной творческой способности и силы мысли. Понятия, созданные тобой, и сейчас остаются ведущими в нашем физическом мышлении, хотя мы теперь и знаем, что если будем стремиться к более глубокому пониманию взаимосвязей, то мы должны будем заменить эти понятия другими, стоящими дальше от сферы непосредственного опыта».

Кинематика дает описание движения, не задавая вопроса о том, почему тело движется именно так, а не иначе. Динамика изучает движение тел в связи с причинами, которые обусловливают тот или иной характер движения. С точки зрения кинематики все системы отсчета равноправны, то есть выбор любой из них допустим для описания движения. Иначе обстоит дело в динамике – разделе механики, изучающем движение, основываясь на анализе его причин.

В основе классической механики лежат три закона динамики, сформулированные Ньютоном. Законы Ньютона, как и все остальные физические законы, возникли в результате обобщения большого количества опытных фактов. Правильность их подтверждается согласием с опытом тех следствий, которые из них вытекают.

Видео:Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Движение по окружности

Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.

Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.

Если угол поворота мал, то ∆ l ≈ ∆ s .

Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Угловая скорость

При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.

Определение. Угловая скорость

Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .

ω = ∆ φ ∆ t , ∆ t → 0 .

Единица измерения угловой скорости — радиан в секунду ( р а д с ).

Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:

Видео:Физика - движение по окружностиСкачать

Нормальное ускорение

При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.

При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.

a n = ∆ v → ∆ t , ∆ t → 0

Модуль центростремительного ускорения можно вычислить по формуле:

a n = v 2 R = ω 2 R

Докажем эти соотношения.

Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .

В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.

По определению ускорения:

a → = ∆ v → ∆ t , ∆ t → 0

Взглянем на рисунок:

Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .

Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:

R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R

При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:

a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .

При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.

Запись центростремительного ускорения в векторной форме выглядит следующим образом:

Здесь R → — радиус вектор точки на окружности с началом в ее центре.

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Тангенциальное ускорение

В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.

Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.

a τ = ∆ v τ ∆ t ; ∆ t → 0

Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t

Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.

Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .

Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω

Видео:Кинематика за 8 минСкачать

I. Механика

Видео:Кинематика точки Движение по окружностиСкачать

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Видео:Физика | Равномерное движение по окружностиСкачать

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Видео:Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Видео:Кинематика: движение по окружности | Физика ЕГЭ 10 класс | УмскулСкачать

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Видео:Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Видео:Кинематика. Движение по окружности. Урок 4Скачать

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Видео:Лекция №1 "Кинематика материальной точки" (Булыгин В.С.)Скачать

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Видео:Физика 10 Равномерное движение точки по окружностиСкачать

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Видео:Вращательное движение. 10 класс.Скачать

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

🔍 Видео

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Кинематика. Движение по окружности. Лекция 1-2Скачать

Cложное движение точки. ТермехСкачать

КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

Термех. Кинематика. Сложное движение точкиСкачать

Кинематика. Решение задач на движение по окружности. Урок 5Скачать