| Фигура | Рисунок | Формулировка | ||||||||
| Прямоугольный треугольник | ||||||||||
| Равнобедренный прямоугольный треугольник | ||||||||||
| Прямоугольный треугольник с углом в 30° |
| Прямоугольный треугольник |
| Равнобедренный прямоугольный треугольник |
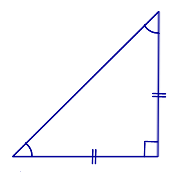 Определение равнобедренного прямоугольного треугольника: Равнобедренным прямоугольным треугольником называют такой прямоугольный треугольник, у которого равны катеты. Свойство углов прямоугольного треугольника: Острые углы равнобедренного прямоугольного треугольника равны 45° . |
| Прямоугольный треугольник с углом в 30° |
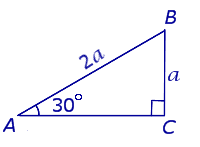 Свойство прямоугольного треугольника с углом в 30° : Катет прямоугольного треугольника, лежащий против угла в 30° , равен половине гипотенузы. Признак прямоугольного треугольника с углом в 30° : Если в прямоугольном треугольнике один из катетов равен половине гипотенузы, то этот катет лежит против угла в 30° . |
| Медиана, проведённая к гипотенузе прямоугольного треугольника |
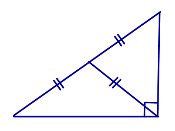 Свойство медианы, проведенной к гипотенузе прямоугольного треугольника: Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы. Признак прямоугольного треугольника: Если в треугольнике медиана равна половине стороны, к которой она проведена, то такой треугольник является прямоугольным. |
| Центр описанной окружности |
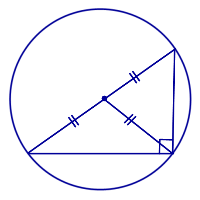 Свойство окружности, описанной около прямоугольного треугольника: Середина гипотенузы прямоугольного треугольника является центром описанной около него окружности. Признак прямоугольного треугольника: Если в треугольнике центр описанной окружности лежит на одной из сторон, то этот треугольник является прямоугольным треугольником, а центр описанной окружности совпадает с серединой гипотенузы. |
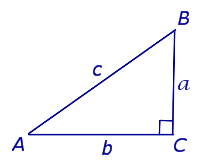 В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов Обратная теорема Пифагора: Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник является прямоугольным Содержание Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать  Прямоугольный треугольникПрямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚). Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника. Стороны, прилежащие к прямому углу, называются катетами . Признаки равенства прямоугольных треугольниковЕсли катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ). Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ). Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ). Свойства прямоугольного треугольника1. Сумма острых углов прямоугольного треугольника равна 90˚. 2. Катет, противолежащий углу в 30˚, равен половине гипотенузы. И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚. 3. Теорема Пифагора:
4. Площадь 5. Высота 6. Центр описанной окружности – есть середина гипотенузы. 7. Радиус 8. Медиана, проведенная к гипотенузе, равна ее половине 9. Радиус Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь. Видео:7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать  Свойства прямоугольного треугольникаВ данной публикации мы рассмотрим определение и свойства прямоугольного треугольника. Также разберем пример решения задачи для закрепления изложенного материала. Видео:№256. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего из катетовСкачать  Определение прямоугольного треугольникаПрямоугольным называют треугольник, в котором один из трех углов является прямым, т.е. равным 90°. Прямоугольный треугольник может быть равнобедренным – когда оба катета равны, а угол между каждым из них и гипотенузой составляет 45°. Видео:Длина гипотенузы прямоугольного треугольника ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать  Свойства прямоугольного треугольникаСвойство 1Сумма двух острых углов прямоугольного треугольника равняется 90°. α + β = 90° Сумма всех углов любого треугольника составляет 180°. Т.к. один угол равен 90°, на два других, также, остается 90°. Свойство 2Катет прямоугольного треугольника, расположенный напротив угла в 30°, равняется половине его гипотенузы. В нашем случае, катет AB лежит напротив ∠ACB = 30°. Следовательно: Если длина одного из катетов прямоугольного треугольника в два раза меньше длины его гипотенузы, значит угол напротив этого катета равняется 30°. Свойство 3Терему Пифагора можно, также, отнести к свойствам прямоугольного треугольника. Согласно ее формулировке, сумма квадратов катетов (a и b) равняется квадрату гипотенузы (c). Таким образом, гипотенуза прямоугольного треугольника больше любого из его катетов. Свойство 4Медиана, опущенная на гипотенузу прямоугольного треугольника (проведенная из вершины прямого угла), равняется половине гипотенузы. Свойство 5Середина гипотенузы прямоугольного треугольника – это центр описанной вокруг него окружности. Согласно свойству 4, рассмотренному выше, медиана BO равняется половине гипотенузы AC и, одновременно, радиусу окружности, описанной вокруг △ABC. Видео:Свойства прямоугольного треугольника. 7 класс.Скачать  Пример задачиВ качестве примера давайте рассмотрим второе свойство, представленное выше. Допустим у нас имеется прямоугольный треугольник ABC с прямым углом в вершине C. Катет BC расположен напротив угла в 30°. Нужно доказать, что BC в два раза меньше гипотенузы AB. Решение Нарисуем чертеж по условиям задачи, и зеркально отразим получившийся треугольник. Получаем △ABD, в котором ∠BAD равен 60° (30° + 30°). Т.к. все три угла данного треугольника равны, он является равносторонним. Следовательно, AD = AB = BD. Отрезки BC и CD равны между собой (зеркально отраженные), и каждый из них составляет половину BD. Как мы уже выяснили, BD равняется AB. Таким образом, BC в два раза меньше AB (или AB = 2BC). 📺 ВидеоКатеты и гипотенузаСкачать  Определение длины гипотенузыСкачать  Доказать, что сумма кубов катетов меньше куба гипотенузыСкачать  Высота, биссектриса, медиана. 7 класс.Скачать  Теорема Пифагора для чайников)))Скачать  Найдите площадь прямоугольного треугольника, если сумма его катетов равна 15, а гипотенуза равна 13Скачать  Площадь треугольника. Как найти площадь треугольника?Скачать  Как найти гипотенузу в прямоугольном треугольнике, минуя теорему Пифагора?Скачать  №485. Найдите катет прямоугольного треугольника, лежащий против угла 60°, если гипотенуза равна с.Скачать  Лайфхак нахождения катета в прямоугольном треугольникеСкачать  Почти никто не решил ➜ Найдите сторону треугольникаСкачать  Катеты прямоугольного треугольника равны 3 и 4. Найдите высоту, проведённую к гипотенузеСкачать  Катеты прямоугольного треугольника равны cosx и sin2. Найдите x, если гипотенуза равна 1Скачать 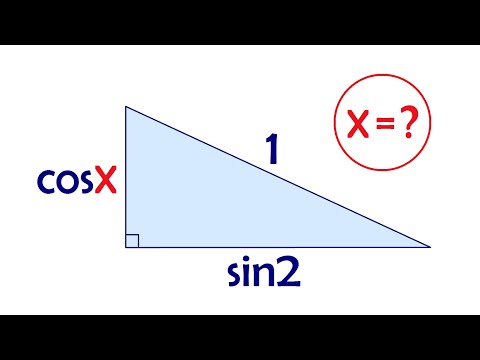 Геометрия Найдите меньший катет прямоугольного треугольника и его высоту, проведенную к гипотенузеСкачать  Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать  |



 Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).












