1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
| A ( ; ), B ( ; ), C ( ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. Содержание Видео:Уравнение прямой и треугольник. Задача про высотуСкачать  Расчет треугольника по координатам вершинЭтот онлайн калькулятор по введенным координатам вершин вычисляет параметры треугольника: длины сторон, углы, периметр и площадь. Этот онлайн калькулятор предназначен для быстрого вычисления ряда характеристик треугольника по координатам его вершин. Вы вводите координаты вершин A, B и C. Калькулятор рассчитывает по координатам следующие величины:
Если нужно что-то еще, пишите в комментариях, добавим. Формулы расчета значений треугольника описаны под калькулятором. Видео:Уравнения стороны треугольника и медианыСкачать  Решение треугольников онлайнС помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже. Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°. Видео:Вычисляем высоту через координаты вершин 1Скачать  Решение треугольника по трем сторонамПусть известны три стороны треугольника a, b, c (Рис.1). Найдем
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения
Пример 1. Известны стороны треугольника ABC: Решение. Из формул (1) и (2) находим:
И, наконец, находим угол C:
Видео:№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать  Решение треугольника по двум сторонам и углу между нимиПусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
Найдем сторону c используя теорему косинусов:
Далее, из формулы
Далее из (3) с помощью калькулятора находим угол A. Поскольку уже нам известны два угла то находим третий:
Пример 2. Известны две стороны треугольника ABC: Решение. Иcпользуя теорму косинусов найдем сторону c:
Из формулы (3) найдем cosA:
Поскольку уже нам известны два угла то находим третий:
Видео:Вычисление медианы, высоты и угла по координатам вершинСкачать  Решение треугольника по стороне и любым двум угламПусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
Так как, уже известны два угла, то можно найти третий:
Далее, для находждения сторон b и c воспользуемся тероемой синусов:
Пример 3. Известна одна сторона треугольника ABC: Решение. Поскольку известны два угла, то легко можно найти третий угол С:
Найдем сторону b. Из теоремы синусов имеем:
Найдем сторону с. Из теоремы синусов имеем: 🎦 Видео№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать  найти уравнение высоты треугольникаСкачать  По силам каждому ★ Найдите стороны треугольника на рисункеСкачать  Почти никто не решил ➜ Найдите сторону треугольникаСкачать  Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать  Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать  Найдите сторону треугольника, если другие его стороны равны 1 и 5Скачать  Аналитическая геометрия на плоскости. Решение задачСкачать  Нахождение стороны прямоугольного треугольникаСкачать  Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать  найти уравнения биссектрис углов между прямымиСкачать  Найдите сторону треугольника на рисункеСкачать  Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать  Уравнения прямой на плоскости | Векторная алгебраСкачать  Нахождение длины отрезка по координатамСкачать  | |||||||||||||||||||||||||||||||||
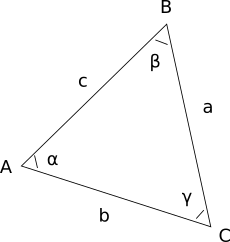Обозначения треугольника
.
.
Найти 
.
.
, 
.
.
.
.
и 
(Рис.2). Найти сторону c и углы A и B.
.
.
.
.
, 
.
, 
.
и углы 
(Рис.3). Найти стороны b и c и угол С.
