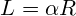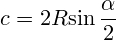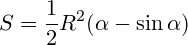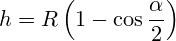Статья содержит два калькулятора, рассчитывающие параметры деления круга на равные по площади части радиусами и параллельными хордами
Ниже представлены два калькулятора, рассчитывающие параметры разделения круга на равные части. Сначала — традиционный калькулятор, который делит круг на равные части радиусами (примерно так, как режут пиццу или торт), под ним — нетрадиционный калькулятор, который делит круг на равные по площади части параллельными хордами. Оба калькулятора визуализируют результат рисунком. Методы расчета с формулами для обоих калькуляторов приведены ниже, под калькуляторами.
Деление круга на равные по площади части радиусами
Деление круга на равные по площади части параллельными хордами
Деление круга на равные части радиусами
Традиционный и очень простой метод деления круга — по факту, нарезка равных секторов. Метод и формулы очень просты:
- Определяем угловой размер каждого сектора в радианах, путем деления 360 градусов на нужное число секторов.
- Определяем размер дуги сектора, перемножая радиус на угол в радианах
- Определяем размер хорды по теореме косинусов (хорда является основанием равнобедренного треугольника с боковыми сторонами R и противолежащим углом альфа.
Собственно и всё — мы получили все характеристики для N равных секторов
Деление круга на равные части параллельными хордами
Этот способ более любопытен, чем предыдущий. Для простоты будем рассматривать верхнюю половину круга, так как с нижней все будет симметрично.
Задача состоит в определении x-вой координаты точек, через которые нужно проводить хорды (на рисунке это точки x1 и x2). Выведем для начала формулу площади куска, отсекаемого хордой слева.
Верхнюю полуокружность можно представить графиком функции y=f(x), где x — это координата вдоль оси абсцисс, а y — это функция, численно равная y координате соответствующей точки верхней полуокружности.
По теореме Пифагора получаем следующую функцию
Чтобы получить площадь фигуры, отсекаемой хордой слева, надо проинтегрировать эту функцию от -R до x. Первообразная функции равна:
Осталось определиться с константой. Нам надо, чтобы в точке с координатами -R площадь была равна нулю. Подставив -R вместо x в формулу выше, получаем
Итак, полное выражение
Теперь рассмотрим нахождение координат крайней левой точки. Нам известна площадь, которую она должна отсечь (напоминаю, речь идет о полуокружности)
Таким образом мы можем приравнять
Что дает нам такое финальное уравнение
Данное уравнение является трансцендентным, а поэтому находить координату первой точки придется численным методом, например, методом бисекции или методом Ньютона. Калькулятор использует метод Ньютона.
Вторая и последующие точки находится аналогично, путем изменения размера отсекаемой площади. Для второй точки это будет , для третьей и так далее.
Зная координаты точек, несложно рассчитать все остальные параметры, в частности, длину хорды.
Видео:Деление окружности на 3 частиСкачать

Сегмент круга
Данный калькулятор считает параметры сегмента круга, а именно:
- длину дуги (L),
- длину хорды (C),
- площадь (S),
- высоту (h),
Перед вами 2 калькулятора, чтобы рассчитать параметры сегмента:
1) сегмент круга решается с помощью радиуса (R) и угла (A).
2) сегмент круга находим с помощью высоты и длины хорды.
Видео:Деление окружностей на равные частиСкачать
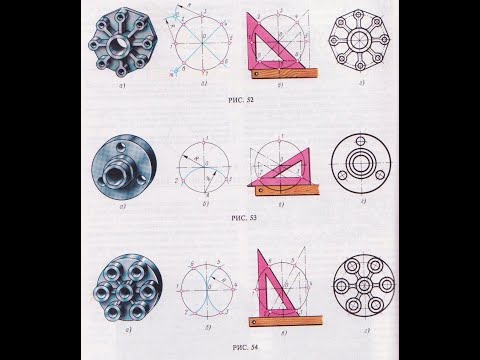
Деление окружности при помощи коэффициента
Для деления окружности на любое число равных частей часто пользуются приведённой в статье таблицей коэффициентов для длин хорд заданной окружности.
Деление окружности на произвольное число равных частей можно производить с помощью таблицы хорд
Для деления окружности на любое число равных частей пользуются коэффициентами, приведёнными в таблице. Длину L хорды, которую откладывают на заданной окружности.
Для получения длины хорды, нужно умножить диаметр окружности на коэффициент из таблицы.
Таблица позволяет делить окружность до 30 частей. Если требуется большее количество, то коэффициент несложно посчитать самостоятельно. Для этого делим 360 на нужное количество частей и берём синус этого числа (на большинстве калькуляторов есть такая функция). Полученный результат делим на два — это и есть наш коэффициент.
📺 Видео
Деление окружности на 3; 6; 12 равных частейСкачать

Деление окружности на равные части. Внимание!!! В таблице имеются ошибки. ПОЛЬЗУЙТЕСЬ ФОРМУЛОЙ!!!Скачать

Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Деление окружности на 12 равных частейСкачать

Деление окружности на n- равные частиСкачать

Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Деление окружности на 3, 4, 5, 6 и 7 равных частейСкачать

Деление окружности на 4 частиСкачать

Деление окружности на 5 частей с помощью циркуляСкачать
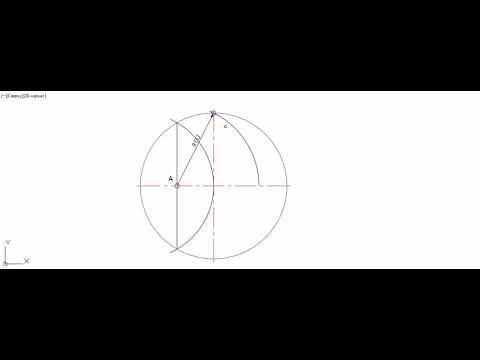
Деление окружности на 7 частейСкачать
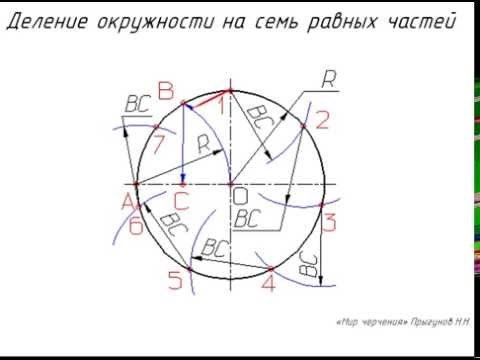
Деление окружностиСкачать

Деление окружности на равные части с помощью циркуляСкачать

Деление окружности на 6 равных частейСкачать

деление окружности на произвольное число частейСкачать
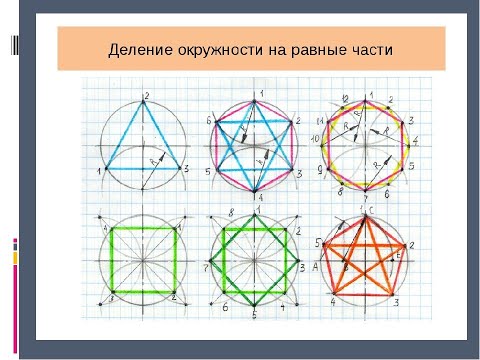
1 2 2 деление окружности на 5 равных частейСкачать

Деление окружности на N равных частей. Урок 8. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

1 2 3 деление окружности на 7 равных частейСкачать

1 2 1 деление окружностиСкачать