| Фигура | Рисунок | Формулировка | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Треугольник |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Большая сторона треугольника |  | Против большей стороны треугольника лежит больший угол | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Больший угол треугольника | Против большего угла треугольника лежит большая сторона | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Меньшая сторона треугольника |  | Против меньшей стороны треугольника лежит меньший угол | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Меньший угол треугольника | Против меньшего угла треугольника лежит меньшая сторона | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Длины сторон треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Углы треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внешний угол треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Больший угол треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Меньший угол треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Теорема косинусов |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Теорема синусов |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Треугольник | ||
 | ||
| Большая сторона треугольника | ||
 | Против большей стороны треугольника лежит больший угол | |
| Больший угол треугольника | ||
 | Против большего угла треугольника лежит большая сторона | |
| Меньшая сторона треугольника | ||
 | Против меньшей стороны треугольника лежит меньший угол | |
| Меньший угол треугольника | ||
 | Против меньшего угла треугольника лежит меньшая сторона | |
| Длины сторон треугольника | ||
 | ||
| Углы треугольника | ||
 | ||
| Внешний угол треугольника | ||
 | ||
| Больший угол треугольника | ||
 | ||
| Меньший угол треугольника | ||
 | ||
| Теорема косинусов | ||
 | ||
| Теорема синусов | ||
 | ||
| Треугольник |
 |
Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.
Определение . Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .

Свойство большей стороны треугольника:
Против большей стороны треугольника лежит больший угол

Свойство большего угла треугольника:
Против большего угла треугольника лежит большая сторона

Свойство меньшей стороны треугольника:
Против меньшей стороны треугольника лежит меньший угол

Свойство меньшего угла треугольника:
Против меньшего угла треугольника лежит меньшая сторона

Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.
a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.

Свойство углов треугольника:
Сумма углов треугольника равна 180°
Свойство внешнего угла треугольника:
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Свойство большего угла треугольника:
Величина большего угла треугольника не может быть меньшей, чем 60°.

где α – больший угол треугольника.

Свойство меньшего угла треугольника:
Величина меньшего угла треугольника не может быть большей, чем 60°.

где β – меньший угол треугольника.


Свойство меньшего угла треугольника:

Видео:наибольшая и наименьшая стороны треугольника. Углы треугольника #углы #треугольникСкачать

Существующие треугольники
Определение
Существующие треугольники — это такие треугольники,
существование которых можно доказать с помощью неравенств.
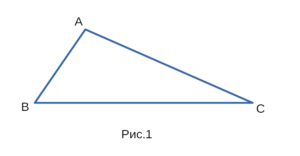
Например существование треугольника, изображенного на рисунке 1,
можно доказать с помощью неравенств: AB + BC > AC, AC + BC > AB, AB + AC > BC
Если эти три неравенства истинны значит треугольник существует,
иначе он не существует.
Также существование того или иного треугольника можно проверить с
помощью одного условия: Если большая сторона треугольника меньше
суммы двух других сторон, значит треугольник существует,
иначе он не существует.
Теорема
Для доказательства того, о чем мы говорили существует теорема под названием неравенство треугольника. Формулировка теоремы:
каждая сторона треугольника меньше суммы двух других сторон.
Докажем, что каждая сторона треугольника, изображенного на рисунке 2, меньше суммы двух других сторон:
Доказательство теоремы
- Проведем отрезок CD равный отрезку CB.
- △BCD — равнобедренный, значит ∠ CBD=∠CDB.
- Рассмотрим △ABD: ∠ ABD >∠ CBD, следовательно ∠ ABD >∠ CDB, то AB
Видео:Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Теорема о соотношении между сторонами треугольника. Доказательство
Во всяком треугольнике любая сторона меньше суммы двух других. Вот наш треугольник ABC. Утверждение теоремы состоит в том, что даже самая длинная его сторона AC — всё равно короче, чем сумма двух других сторон AB и BC. Для доказательства этого утверждения проведём высоту из вершины большего угла B. В каждом полученном прямоугольном треугольнике гипотенуза больше катета , и две гипотенузы в сумме больше большой стороны. Каждая из маленьких сторон (то есть AB или BC) — меньше, чем AC, и понятное дело, меньше суммы двух других сторон. ЧТД.
💡 Видео
Найдите сторону треугольника, если другие его стороны равны 1 и 5Скачать

Уравнения стороны треугольника и медианыСкачать

7 класс, 33 урок, Теорема о соотношениях между сторонами и углами треугольникаСкачать

Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Задача про соотношение сторон. Геометрия 7 класс.Скачать

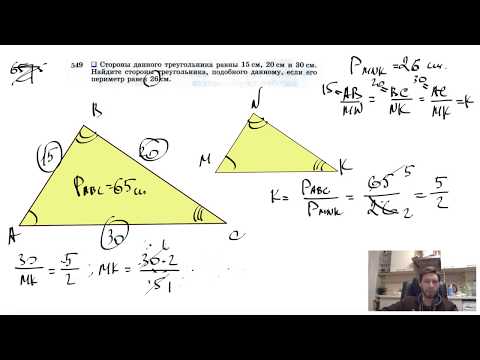
№549. Стороны данного треугольника равны 15 см, 20 см и 30 см. Найдите стороны треугольникаСкачать
ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Почему каждая сторона треугольника меньше суммы двух других сторон?Скачать

Найдите сторону треугольника на рисункеСкачать

№156. Периметр треугольника ABC равен 15 см. Сторона ВС больше стороны АВ на 2 см, а сторона ABСкачать

Геометрия Стороны треугольника равны 17 см 65 см и 80 см Найдите наименьшую высоту треугольникаСкачать

№237. Сравните стороны треугольника ABC, если: a) ∠A∠B∠C; б) ∠A∠B=∠C.Скачать

Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Неравенство треугольника ★ Любая сторона треугольника меньше суммы двух других сторонСкачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать