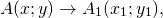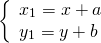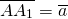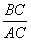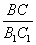Видео:Геометрия 9 класс (Урок№29 - Параллельный перенос.)Скачать

We are checking your browser. mathvox.ru
Видео:Параллельный перенос точки, отрезка, треугольника, четырехугольника. Геометрия 8 классСкачать

Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
Видео:9 класс, 32 урок, Параллельный переносСкачать

What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Cloudflare Ray ID: 6dd145755fde8e77 • Your IP : 85.95.188.35 • Performance & security by Cloudflare
Видео:11 класс, 12 урок, Параллельный переносСкачать

Параллельный перенос
Параллельный перенос — это преобразование плоскости, при котором точки смещаются в одном и том же направлении на одно и то же расстояние.
Строгое определение параллельного переноса даётся либо через декартовы координаты, либо через вектор.
1) Введём на плоскости декартовы координаты x, y.
Параллельный перенос — это такое преобразование фигуры F, при котором её произвольная точка (x;y) переходит в точку (x+a; y+b), где a и b — некоторые числа, одинаковые для всех точек (x;y) фигуры F.
Формулы параллельного переноса

то параллельный перенос задаётся формулами:
Говорят также, что A1 является образом точки A при параллельном переносе на вектор (a; b). Точка A называется прообразом.
2) Параллельный перенос на данный вектор ā называется отображение плоскости на себя, при котором каждая точка A отображается в такую точку A1, то вектор AA1 равен вектору ā:
Свойства параллельного переноса
1) Параллельный перенос есть движение (то есть параллельный перенос сохраняет расстояние).
2) При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.
3) При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя).
4) Каковы бы ни были точки A и A1, существует единственный параллельный перенос, при котором точка A переходит в точку A1.
В алгебре параллельный перенос широко используется для построения графиков функций.
Видео:Параллельный переносСкачать

Параллельный перенос, поворот плоскости и подобные треугольники
Корзина

Теоретический урок по предмету математики для решения задач по теме «Параллельный перенос, поворот плоскости и подобные треугольники».
Содержание данной онлайн страницы электронного справочника для школьников:
- – тема «Параллельный перенос» представлена на примере решения задач 145 — 148;
- – в контрольных работах с номерами 149 — 154 данной рабочей тетради по математике рассматривается поворот плоскости вокруг точки на угол;
- – повторение курса геометрии 9 класса в решениях приведено на примере заданий 155 — 173: углы треугольника, площадь треугольника через катеты и гипотенузу, вычисление радиуса описанной окружности, стороны ромба, подобные треугольники.
Видео:Параллельный перенос. Симметрия. Поворот | МатематикаСкачать

Параллельный перенос


Параллельным переносом на вектор 


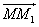

Задача 145.



A → A1 : 


B → B1 : 


Теорема:
При параллельном переносе на вектор 

f – параллельный перенос на вектор 
M 

N 



Точка M переводится движением в точку M1 с условием, что два вектора равны: M 



Точка N переводится движением в точку N1 с условием, что два вектора равны: N 



Следовательно, полученные отрезки параллельны MM1 || NN1 и построенные отрезки равны MM1 = NN1
Значит, четырехугольник MM1N1N – параллелограмм.
Поэтому MN = M1N1, значит f – движение.

Задача 146.
A 




B 




C 


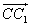


A 




B 




C 


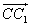



Задача 147.
точка D лежит на AC: D 
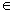
точка C лежит на AD: C 
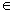
BC 
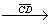
б) Доказать: ABB1D – равнобедренная трапеция
1) От точки B проведем прямую a, параллельную вектору 
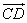

2) Точка B переводится движением в точку B1



3) Проведем прямую B1D, параллельную отрезку BC:
Рассмотрим четырехугольник BB1DC.
Т.к. основания BB1 || CD и боковые стороны BC || BD параллельны, то BB1DC – параллелограмм (по определению)
По свойству параллелограмма:
основания BB1 = CD и боковые стороны BC = BD равны, но AB = BC, тогда AB = B1D
Т.к. BB1 || AD параллельны и AB 
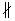
Т.к. AB = B1D, то ABB1D – равнобедренная трапеция.
Задача 148.
Дано: 
вектор 
окр (O;R) 

ΔABC 

EFPQ 

как показано на рисунке.
Видео:6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

Поворот плоскости вокруг точки на угол
Определение:




O – центр поворота
α – угол поворота
Задача 149.


α = 75° (против часовой стрелки)
O – центр поворота
1) A 
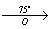


2) B 
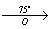


Теорема:
Поворот является движением.


α – угол поворота (против часовой стрелки)
точка O – центр поворота
Тогда треугольники равны ΔOMN = ΔOM1N1 по двум сторонам и углу между ними:




Тогда MN = M1N1, значит, f – движение.
Задача 150.
точка O – центр поворота


1) A 
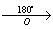


2) B 
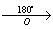


Задача 151.
точка A – центр поворота
α = 160° (против часовой стрелки)
1) B 
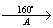


2) C 
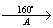


Задача 152.
точка O – центр поворота


1) A 
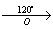


2) B 
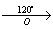


Задача 153.
точка C – центр окружности (C; R)
точка O – центр поворота
угол поворота α = 60° (против часовой стрелки)
а) точка C и точка O не совпадают
б) точка C и точка O совпадают


1) проведем луч CO
2) C 
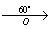



Т.к. точка О – центр поворота и точка С – центр окружности совпадают, то окружности (C;R) и (C1;R) будут тоже совпадать.

Задача 154.
Δ ABC – равнобедренный, равносторонний
D – точка пересечения биссектрис
D – центр поворота
угол поворота α = 120°
ΔABC 

Т.к. Δ ABC – правильный, то все углы в нем равны 60°.
Т.к. точка D – центр описанной и вписанной окружности, то
Δ ABD = Δ BDC = Δ DAC (по трем сторонам).
Следовательно, что 





A 

B 

C 

Таким образом, Δ ABC отображается на себя.
Повторение.
Задача 155.






Найти: наибольший угол треугольника
Пусть x – коэффициент пропорциональности. Зная, что сумма углов в треугольнике равна 180°, составим и решим уравнение:
3x + 7x + 8x = 180
Наибольший угол 

Задача 156.
треугольник ΔABC – равнобедренный,
один угол больше другого:






Найти: угол при основании треугольника
Пусть x° – угол при основании треугольника. Зная, что сумма углов в треугольнике составляет 180°, составим и решим уравнение:
(x + 60°) + x + x = 180°
Значит, 

Задача 157.
треугольник ΔABC – прямоугольный
c = 26 см – гипотенуза
Найти: больший катет b
Пусть x – коэффициент пропорциональности. По теореме Пифагора составим и решим уравнение:
(5x) 2 + (12x) 2 = 26 2
25x 2 + 144x 2 = 676
b = 12 • 2 = 24 (см)
Задача 158.


c = 13 – гипотенуза
По теореме Пифагора получаем:
a = 
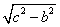

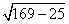

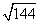
Тогда площадь треугольника
SΔABC = 


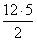
= 30 (квадратных единиц)
Задача 159.
треугольник ΔABC – равнобедренный,


c = 4 
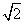
Найти: площадь треугольника SΔABC = ?
SΔABC = 

Т.к. Δ ABC – равнобедренный, то углы при основании по 45° и катеты равны a = b.
По теореме Пифагора получаем:
Тогда (4 
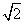
Тогда площадь треугольника
SΔABC = 


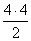
= 8 (квадратных единиц)
Задача 160.




Найти: радиус описанной окружности R = ?
Т.к. AH – медиана, то CH = 

По теореме Пифагора получаем:
Тогда CH = 


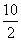
Точка H – центр описанной окружности
Т.к. R = AH, то R = AH = CH = 5 ед.
Задача 161.


соотношение острых углов




AC = 4 
Найти: радиус описанной окружности R = ?


Тогда 



Следовательно, BC = 

По теореме Пифагора получаем:
AC 2 + 
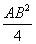
AC 2 = 

AB 2 = 
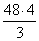
R = AD = BD = 8 : 2 = 4 (ед)
Задача 162.




радиус описанной окружности
Тогда AB = 2,5 • 2 = 5
По теореме Пифагора получаем:
AC = 
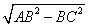

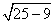

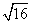




tg 


0,6 = 
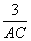

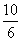
Задача 164.


Найти: 



Т.к. AH = AC, то Δ AHC – равнобедренный.
Точка H – радиус вписанной окружности, поэтому AH = CH, но AH = AC, следовательно, AH = CH = AC.
Тогда Δ AHC – равносторонний.
Значит, 





Задача 165.
треугольник Δ ABC – правильный, равносторонний,
SΔABC = 
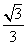
Найти: длину биссектрисы BH = ?


Рассмотрим Δ ABC – равнобедренный, где




Тогда BH – медиана, высота.
Значит, перпендикулярны отрезки BH 
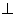
Рассмотрим треугольники Δ ABH и Δ BHC.
AB = BC, по условию.
AH = CH, BH – медиана.
Значит, треугольники равны Δ ABH = Δ BHC.
Т.е. SΔABH = 




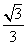

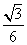
SΔABH = 

Рассмотрим треугольник Δ ABH.
Т.к. BH – биссектриса, то угол 

AH = 

SΔABH = 


AB • BH = 

По теореме Пифагора получаем:
AB 2 = AH 2 + BH 2
AB 2 = 

BH 2 = 

BH = 
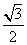
Используя результат (**) в уравнении (*), получаем
AB • 
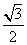

AB 2 = 
AB = 
Тогда AB • BH = 






Задача 166.
треугольник Δ ABC – правильный, равносторонний,


R = 
Найти: площадь треугольника
Рассмотрим Δ ABO (AO = BO = R) 

Проведем из вершины O к AB высоту OH.
Рассмотрим Δ AOH, где 

Т.к. 







OH = 


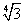

По теореме Пифагора получаем:
OH 2 + AH 2 = OA 2

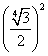

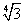



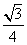
= 
AH 2 = 
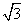

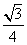

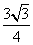



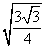

Тогда площадь треугольника
SΔAOH = 




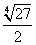

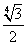

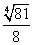

Следовательно, SΔABO = 2 • SΔAOH = 2 • 
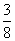


Тогда площадь треугольника
SΔABC = 3 • SΔABO = 3 • 


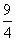




Площадь ромба SABCD = 384
Соотношение диагоналей ромба:
Найти: сторону ромба AB = ?
SABCD = 

Пусть x – коэффициент пропорциональности. Тогда
SABCD = 

Следовательно, диагональ BD = 4x = 4 • 8 = 32
AC = 3x = 3 • 8 = 24
Поэтому половина диагонали AO = 



BO = 



По теореме Пифагора получаем:
AO 2 + BO 2 = AB 2
Сторона ромба AB = 
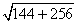

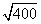
Задача 168.
треугольник Δ ABD – равнобедренный,


Найти: площадь треугольника
SΔABD = 

Проведем высоту BH к основанию AD.
По свойству равнобедренного треугольника:
BH – медиана, биссектриса, высота.
Т.к. BH – медиана, то AH = DH = 16 : 2 = 8 (ед.)
Рассмотрим треугольник Δ ABH, где угол 

По теореме Пифагора получаем:
AB 2 = AH 2 + BH 2
BH = 
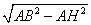

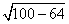

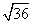
Тогда площадь треугольника
SΔABD = 



Ответ: площадь треугольника SΔABD = 48 кв.ед.

Задача 169.
треугольник Δ ABC –равнобедренный,
основание AC больше высоты BH на 15: AC > BH на 15
Найти: основание AC = ?
Т.к. треугольник Δ ABC –равнобедренный, то BH – высота, медиана, биссектриса.
Тогда AC = AH + CH = AH + AH = 2 AH
Рассмотрим Δ ABH – прямоугольный.
Пусть AC = (x) ед. 


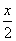
Тогда AB = (x – 15) ед. (по условию).
По теореме Пифагора решим уравнение:
(x – 15) 2 = ( 
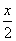



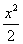
4 (x 2 – 30x) = x 2
4x 2 – 120x = x 2
3x 2 – 120x = 0 | : x
Таким образом, 40 ед. – длина основания.
Ответ: AC = 40 ед.
Видео:ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС И ПОВОРОТ 9 класс геометрия АтанасянСкачать

Подобные треугольники
Задача 170.






CH – биссектриса угла 

Доказать: подобие треугольников
Δ BHC 









Т.к. CH – биссектриса угла 





Рассмотрим Δ BHC








Тогда 



Поэтому треугольники подобны Δ BHC 



верхнее основание BC = 4 см
нижнее основание AD = 10 см
диагональ BD = 8 см
часть диагонали BO = ?
соотношение периметров треугольников


Углы равны 



Углы равны 



Тогда треугольники подобны Δ BCO 




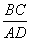

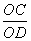







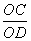













Пусть BO = x, AO = 8 – x. Тогда 10x = 4 • (8 – x)
x = 2 

Следовательно, BO = 2 



Ответ: BO = 2 



Задача 172.
ΔABC 



P (ΔABC) = 12 +16 + 20 = 48 (дм)
Т.к. треугольники подобны, то

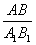

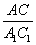




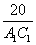


Тогда соотношение периметров треугольников

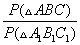
Из равенств (*) и (**) следует



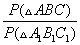




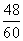

B1C1 = 
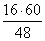
Тогда 





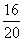



A1B1 = 
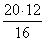
Задача 173.


стороны трапеции пересекаются в точке M:
Рассмотрим треугольники ΔAMD и ΔBMC:








Тогда, по первому признаку подобия треугольников:
треугольники подобны Δ AMD 


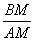

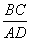

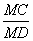


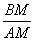

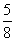
но AM = AB + BM = 3,9 + BM
8 • BM = 5 (3,9 + BM)

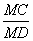

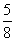
💡 Видео
Перенос треугольника по векторуСкачать
Параллельные прямые циркулемСкачать

Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать

Геометрия 9 класс : Параллельный перенос и поворотСкачать

Геометрия 9 класс (Урок№30 - Поворот.)Скачать

Определение преобразований | Геометрические преобразования и Конгруэнтность | ГеометрияСкачать

#192 ПОВОРОТ И ПЕРЕНОС // ТРЕУГОЛЬНИКСкачать

Движения. Симметрии. Параллельный перенос. Поворот. Урок 13. Геометрия 9 классСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

115 Параллельный переносСкачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Урок 8. Параллельный перенос. Декартовы координаты на плоскости.Скачать