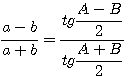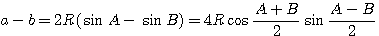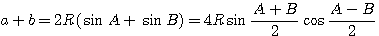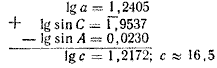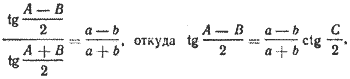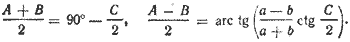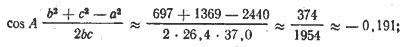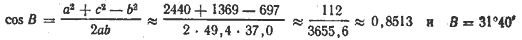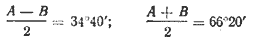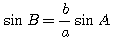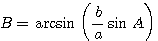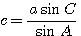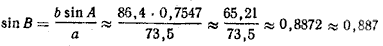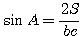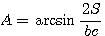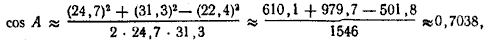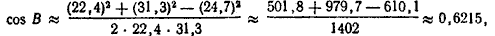Как решить косоугольный треугольник (4 видео)

Решение косоугольных треугольников

Содержание

Решение треугольника по двум его углам и стороне
Решение треугольника по двум сторонам и углу между ними
Решение треугольника по двум сторонам и углу, противолежащему одной из них
Как решить косоугольный треугольник
Что такое косые треугольники? (с решенными упражнениями)
Косые треугольники
Законы груди и косинуса
обучение
Первое упражнение
Второе упражнение
Третье упражнение
Четвертое упражнение
🔥 Видео

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Решение треугольника по двум его углам и стороне

Задача. Даны два угла треугольника и сторона, прилежащая к ним; вычислить другие стороны и угол.

Даны В, С и а; требуется найти b, с и А.

Решение. Условие возможности построения треугольника по этим данным:

А + В 1 /_0,9483 ≈ 1,055.

Вычисления выполнены по правилам приближённых вычислений. Значения синусов взяты из таблиц Брадиса; во всех промежуточных результатах сохраняются четыре значащие цифры (правило запасной цифры), а окончательный результат округлён до трёх значащих цифр.

Решение при помощи логарифмических таблиц. Имеем:

b = a sin B /_{sin A}, lg b = lg a + lg sin В — lg sin A.

По таблицам найдем:

lg a = 1,2405, lg sinB = 1,8457, ld sin A = 1,9770, откуда lg b = 1,1092

По таблицам Брадиса найдём b = 12,86. Однако в ответе следует оставить три значащие цифры, так как значение а дано с тремя значащими цифрами; поэтому b ≈ 12,9.

Сторона с вычисляется аналогично:

c = a sin C /_{sin A}, lg c = lg a + lg sin C — lg sin A.

. lg c = 1,2172; c ≈ 16,5

Видео:9 класс, 15 урок, Решение треугольниковСкачать

Решение треугольника по двум сторонам и углу между ними

Задача. Даны две стороны треугольника и угол между ними; вычислить третью сторону и два других угла.

Пусть, например, даны а, b и С, требуется вычислить А, В и с.

Решение при помощи натуральных таблиц. Формула косинусов даёт выражение стороны с непосредственно через известные элементы:

Для вычисления А можно также воспользоваться формулой косинусов:

Разность углов A — В можно вычислить, воспользовавшись теоремой тангенсов:

Углы А и В определяются из системы уравнений:

Сторону с можно вычислить по теореме синусов:

Пример. Дано: а ≈ 49,4; b ≈ 26,4; С ≈ 47°20 найти А, В и с.

Решение при помощи натуральных таблиц. Имеем:

с 2 = а 2 + b 2 — 2ab cos С ≈ 49,4 2 + 26,4 2 — 2 • 49,4 • 26,4 • cos 47°20&#146

По таблицам квадратов найдём:

а 2 ≈ (49,4) 2 ≈ 2449; b 2 ≈ (26,4) 2 ≈ 697,0

2 • 49,4 • 26,4 • cos 47°20&#146 ≈ 2 • 49,4 • 2,64 • 0,6778 ≈ 1768.

Следовательно, с 2 ≈ 2440 + 697 — 1768 ≈ 1369. По таблицам квадратных корней

А ≈ arc cos (-0,191); угол А — тупой.

Находим дополнительный угол

180° — А ≈ arc cos (0,091) ≈ 79°; А ≈ 180° — 79° = 101°

(с округлением до 10&#146). Наконец,

Решение при помощи логарифмических таблиц. Вычислим углы A и В.

$$ lg tgfrac=lg(a-b) + lg ctgfrac — lg(a+b) $$
$$ lg tgfrac=1,8403 ;;и;; fracapprox 34°40&#146 $$

Из системы уравнений

найдём: A ≈ 101°, В ≈ 31°40&#146.

Видео:КАК РЕШИТЬ ТРЕУГОЛЬНИК?Скачать

Решение треугольника по двум сторонам и углу, противолежащему одной из них

Задача. Даны две стороны треугольника и угол А, лежащей против одной из них; вычислить третью сторону и два остальных угла.

Пусть даны a, b и А; требуется вычислить B, С и с

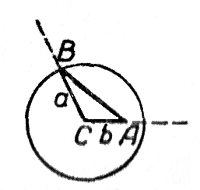
С л у ч а й 1. а > b, т. е, заданный угол А лежит против большей стороны.

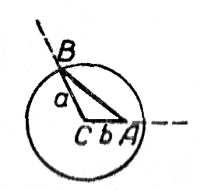
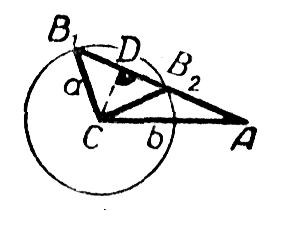
Построение показано на чертеже. Из точки С (как из центра), взятой на одной из сторон угла А на расстоянии b от вершины, описана окружность радиуса а; точка В есть точка пересечения этой окружности с другой стороной угла А.
Построение всегда возможно, задача имеет единственное решение.

Острый угол В, противолежащий меньшей стороне, находится по теореме синусов:

и затем С = 180° — (A + В). Сторона с находится по теореме синусов: ( c=frac )

С л у ч а й 2. а 90° задача не имеет решения.
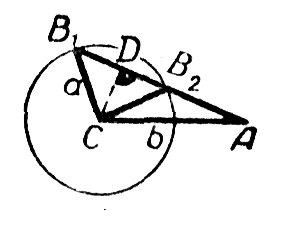
Пусть угол А острый. Из построения на чертеже a), видно, что окружность радиуса а с центром в точке С пересечёт другую сторону угла А в двух точках при условии а > CD, где D — основание перпендикуляра, опущенного из точки С на другую сторону угла A. Так как CD = b sinA (из треугольника ACD), то условие запишется так: a >b sinA.

Для угла В возможны два значения: В = В₁ (острый) и В = В₂ (тупой). Задача имеет два решения.

a) Значения угла В вычисляются по теореме синусов: ( sinB = fracsinA )

Из чертежа видно, что при CD = b sinА > а окружность не пересечёт другой стороны угла А; задача не имеет решений.

При CD = b sin А задача имеет единственное решение: треугольник ABC прямоугольный.

Случай 3. а = b. В этом случае треугольник ABC равнобедренный. Такой треугольник можно решить, разбразбив его высотой CD на два прямоугольных треугольника:

В = А; С = 180° — 2А; с = 2AD = 2а cos A.

Пример. Вычислить стороны и углы треугольника, если дано:

(деление на 73,5 можно заменить умножением на 1 /_73,5 ≈ 0,0136).

Так как в данном случае а b sin A /_a а + b, то треугольник с данными сторонами не существует. Будем считать, что с 2 =b 2 + с 2 — 2bc cos А
b 2 =c 2 + a 2 — 2ca cos B, откуда

Угол А острый, так как он лежит против меньшей стороны; следовательно,

Точно также ( B = arcsinfrac ) и, наконец, С = 180° — (А + В)

Итак, при решении треугольника по трём сторонам при помощи логарифмических таблиц углы, лежащие против меньших сторон, находятся по формулам, а угол, лежащий против наибольшей стороны, вычисляется как разность между 180° и суммой двух найденных углов.

Пример. Решить треугольник, зная длины (приближенные) его сторон: 24,7; 22,4 и 31,3. Обозначим a ≈ 22,4; b ≈ 24,7; с ≈ 31,3.

Решение при помощи натуральных таблиц. Имеем:

откуда А ≈ 45°20&#146 (с округлением до 10&#146).

откуда В ≈ 51°30&#146 и, наконец, С ≈ 180° — (45°20&#146 + 51°30&#146) ≈ 83°10&#146.

Решение при помощи логарифмических таблиц. Имеем:

sin А = 2S /_bc, lg sin А = lg 2S — lg b — lg c.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Как решить косоугольный треугольник

Г л а в а П. Решение косоугольных треугольников

§7(41). Теорема тангенсов

Теорема. Разность двух сторон треугольника относится к их сумме, как тангенс полуразности противолежащих углов к тангенсу полусуммы этих углов:

(и две аналогичные формулы для прочих пар сторон а, с и b, с).

Доказательство. В силу теоремы синусов имеем:

Разделив почленно эти равенства, получим доказываемую формулу.

§8(42). Решение треугольника по двум его углам и стороне

Задача. Даны два угла треугольника и сторона, прилежащая к ним; вычислить другие стороны и угол.
Даны В, С и а; требуется найти b, с и А.

Решение. Условие возможности построения треугольника по этим данным:
А + В 1 /_0,9483 ≈ 1,055.

Решение при помощи логарифмических таблиц. Имеем:

b = a sin B /_{sin A}, lg b = lg a + lg sin В — lg sin A.

По таблицам найдем:

Сторона с вычисляется аналогично:

c = a sin C /_{sin A}, lg c = lg a + lg sin C — lg sin A.

§9(43). Решение треугольника по двум сторонам и углу между ними

Задача. Даны две стороны треугольника и угол между ними; вычислить третью сторону и два других угла.

Пусть, например, даны а, b и С, требуется вычислить А, В и с.

с = / а 2 + b 2 — 2ab cos С

Для вычисления А можно также воспользоваться формулой косинусов:

Разность углов A — В можно вычислить, воспользовавшись теоремой тангенсов:

Углы А и В определяются из системы уравнений:

Сторону с можно вычислить по теореме синусов:

Пример. Дано: а ≈ 49,4; b ≈ 26,4; С ≈ 47°20′; найти А, В и с.

Решение при помощи натуральных таблиц. Имеем:

с 2 = а 2 + b 2 — 2ab cos С ≈ 49,4 2 + 26,4 2 — 2 • 49,4 • 26,4 • cos 47°20′

По таблицам квадратов найдём:

а 2 ≈ (49,4) 2 ≈ 2449; b 2 ≈ (26,4) 2 ≈ 697,0

2 • 49,4 • 26,4 • cos 47°20′ ≈ 2 • 49,4 • 2,64 • 0,6778 ≈ 1768.

Следовательно, с 2 ≈ 2440 + 697 — 1768 ≈ 1369. По таблицам квадратных корней
с ≈ 37,0. Далее

А ≈ arc cos (—0,191); угол А — тупой.

Находим дополнительный угол

180° — А ≈ arc cos (0,091) ≈ 79°; А ≈ 180° — 79° = 101°

(с округлением до 10′). Наконец,

Решение при помощи логарифмических таблиц. Вычислим углы A и В.

Из системы уравнений

найдём: A ≈ 101°, В ≈ 31°40′.

§ 10 (44). Решение треугольника по двум сторонам и углу,
противолежащему одной из них

Пусть даны a, b и А; требуется вычислить B, С и с

С л у ч а й 1. а > b, т. е, заданный угол А лежит против большей стороны.

Острый угол В, противолежащий меньшей стороне, находится по теореме синусов:

откуда

и затем С = 180° — (A + В). Сторона с находится по теореме синусов:

С л у ч а й 2. а 90° задача не имеет решения.
Пусть угол А острый. Из построения на чертеже a) , видно, что окружность радиуса а с центром в точке С пересечёт другую сторону угла А в двух точках при условии а > CD, где D — основание перпендикуляра, опущенного из точки С на другую сторону угла A. Так как CD = b sin A (из треугольника ACD), то условие запишется так: a >b sinA. Для угла В возможны два значения: В = В₁ (острый) и В = В₂ (тупой). Задача имеет два решения.

Значения угла В вычисляются по теореме синусов:

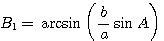
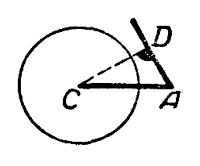
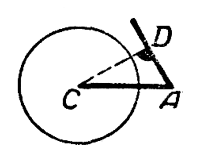
откуда и B₂ = 180° — B₁ Значения угла С и стороны с вычисляются так же, как в предыдущем случае.

Из чертежа b) видно, что при
CD = b sin А > а окружность не пересечёт другой стороны угла А; задача не имеет решений.

В этом случае 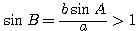и угол В вычислить нельзя.

При CD = b sin А задача имеет единственное решение: треугольник ABC прямоугольный.

В = А; С = 180° — 2А; с = 2AD = 2а cos A.

Пример. Вычислить стороны и углы треугольника, если дано:

(деление на 73,5 можно заменить умножением на 1 /_73,5 ≈ 0,0136, табл. 11).

Так как в данном случае а b sin A /_a а + b, то треугольник с данными сторонами не существует. Будем считать, что с 2 =b 2 + с 2 — 2bc cos А
b 2 =c 2 + a 2 — 2ca cos B, откуда

и (так как 0° / р (р — а)(р — b) (р — с) , где р = (а+ b+c)/2

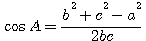
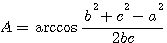
Имеем далее: S = 1 /₂ bc sin A. откуда

Угол А острый, так как он лежит против меньшей стороны; следовательно,

Точно также 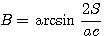и, наконец, С = 180° — (А + В)

Итак, при решении треугольника по трём сторонам при помощи логарифмических таблиц углы, лежащие против меньших сторон, находятся по формулам, а угол, лежащий против наибольшей стороны, вычисляется как разность между 180е и суммой двух найденных углов.

Пример. Решить треугольник, зная длины (приближенные) его сторон: 24,7; 22,4 и 31,3. Обозначим a ≈ 22,4; b ≈ 24,7; с ≈ 31,3.

Решение при помощи натуральных таблиц. Имеем:

откуда А ≈ 45°20′ (с округлением до 10′).

откуда В ≈ 51°30′ и, наконец, С ≈ 180° — (45°20′ + 51°30′) ≈ 83°10′.

Решение при помощи логарифмических таблиц. Имеем:

sin А = 2S /_bc, lg sin А = lg 2S — lg b — lg c.

Решить косоугольные треугольники по заданным основным элементам. (Решение каждого примера следует выполнить при помощи таблиц логарифмов и логарифмической линейки.)

81 (347). Даны сторона и два угла:

1) а ≈ 370,0; В ≈ 86°30′; С ≈ 50°50′

2) а ≈ 450,0; А ≈ 87°50′; В ≈ 10°50′.

3) а ≈ 951; B ≈ 126°40′; С ≈ 13°20′.

4) b ≈ 13,02; A ≈ 11°46′; B ≈ 133°40′.

82 (348). Даны две стороны и угол между ними:

1) а ≈ 510; b ≈ 317; С ≈ 76°10′.

2) а ≈ 225; b ≈ 800; С ≈ 36°40′.

3) а ≈ 2,296; с ≈ 1,687; В ≈ 29°52′.

4) b ≈ 28; c ≈ 42; А ≈ 124°.

83 (349). Даны две стороны и угол против одной из них:

2) b ≈ 360; с ≈ 309; С ≈ 21°30′.

3) а ≈ 13,89; с ≈ 8,42; А ≈ 126°41′.

4) а ≈ 13,81; с ≈ 8,14; С ≈ 14°37′.

5) b ≈ 263,1; с ≈ 215,4; В ≈ 70°14′.

6) а ≈ 19,06; b ≈ 88,19; А ≈ 31°17′.

84 (350). Даны три стороны:

85 (351). Решить косоугольные треугольники по заданным моментам:

1) R ≈ 7,92; А ≈ 113°17′; В ≈ 48°16′.

2) S ≈ 501,9; А ≈ 15°28′; B ≈ 45°23′.

5) а + b ≈ 488,8; А ≈ 70°24′; В ≈ 40°16′.

Видео:КАК РЕШИТЬ ТРЕУГОЛЬНИК?Скачать

Что такое косые треугольники? (с решенными упражнениями)

косые треугольники это те треугольники, которые не являются прямоугольниками. Таким образом, треугольники таковы, что ни один из его углов не является прямым углом (его измерение составляет 90º).

Не имея прямого угла, теорема Пифагора не может быть применена к этим треугольникам.

Поэтому, чтобы узнать данные в косом треугольнике, необходимо использовать другие формулы.

Формулы, необходимые для решения косоугольного треугольника, представляют собой так называемые законы синусов и косинусов, которые будут описаны позже..

В дополнение к этим законам всегда можно использовать тот факт, что сумма внутренних углов треугольника равна 180º..

Видео:9 класс. Геометрия. Решение треугольниковСкачать

Косые треугольники

Как было сказано в начале, наклонный треугольник — это такой треугольник, что ни один из его углов не составляет 90º..

Задача определения длины сторон косоугольного треугольника, а также измерения его углов называется «разрешением косоугольных треугольников»..

Важным фактом при работе с треугольниками является то, что сумма трех внутренних углов треугольника равна 180º. Это общий результат, поэтому для косых треугольников это также может быть применено.

Законы груди и косинуса

Дан треугольник ABC со сторонами длины «a», «b» и «c»:

— Закон груди гласит, что a / sin (A) = b / sin (B) = c / sin (C), где A, B и C — углы, противоположные «a», «b» и «c» соответственно.

— Закон косинусов гласит: c² = a² + b² — 2ab * cos (C). Эквивалентно, могут использоваться следующие формулы:

b² = a² + c² — 2ac * cos (B) или a² = b² + c² — 2bc * cos (A).

Используя эти формулы, вы можете рассчитать данные треугольника под углом.

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

обучение

Вот некоторые упражнения, в которых вы должны найти недостающие данные данных треугольников из определенных предоставленных данных..

Первое упражнение

Учитывая треугольник ABC такой, что A = 45º, B = 60º и a = 12см, вычислите другие данные треугольника..

решение

Используя, что сумма внутренних углов треугольника равна 180º, вы должны

C = 180º-45º-60º = 75º.

Три угла уже известны. Затем перейдите к использованию закона груди, чтобы вычислить две отсутствующие стороны.

Представленные уравнения: 12 / грех (45º) = b / грех (60º) = с / грех (75º).

Из первого равенства вы можете очистить «б» и получить, что

b = 12 * грех (60º) / грех (45º) = 6√6 ≈ 14,696 см.

Вы также можете очистить «с» и получить это

с = 12 * грех (75º) / грех (45º) = 6 (1 + √3) ≈ 16 392 см.

Второе упражнение

Учитывая, что треугольник ABC такой, что A = 60º, C = 75º и b = 10см, рассчитайте другие данные треугольника..

решение

Как и в предыдущем упражнении, B = 180º-60º-75º = 45º. Кроме того, при использовании закона груди необходимо, чтобы a / sin (60º) = 10 / sin (45º) = c / sin (75º), из которого получается, что a = 10 * sin (60º) / sin (45º). = 5√6 ≈ 12,247 см и c = 10 * sin (75º) / sin (45º) = 5 (1 + √3) ≈ 13,660 см.

Третье упражнение

Учитывая, что треугольник ABC такой, что a = 10см, b = 15см и C = 80º, рассчитайте другие данные треугольника.

решение

В этом упражнении известен только один угол, поэтому вы не можете начать, как в предыдущих двух упражнениях. Кроме того, закон груди не может быть применен, потому что никакое уравнение не может быть решено.

Поэтому мы приступаем к применению закона косинусов. Именно тогда

c² = 10² + 15² — 2 (10) (15) cos (80º) = 325 — 300 * 0,173 ≈ 272,905 см,

так что с ≈ 16,51 см. Теперь, зная 3 стороны, закон груди используется, и вы получаете

10 / грех (А) = 15 / грех (В) = 16,51 см / грех (80º).

Отсюда, при очистке B получается без (B) = 15 * sin (80º) / 16,51 ≈ 0,894, что означает, что B ≈ 63,38º.

Теперь можно получить, что A = 180º — 80º — 63,38º ≈ 36,62º.

Четвертое упражнение

Стороны наклонного треугольника: а = 5 см, b = 3 см и с = 7 см. Рассчитать углы треугольника.

решение

Опять же, закон груди не может быть применен напрямую, так как никакое уравнение не будет служить для получения значения углов.

Используя закон косинуса, мы получаем, что c² = a² + b² — 2ab cos (C), где, когда мы очищаем, получаем, что cos (C) = (a² + b² — c²) / 2ab = (5² + 3²-7²) / 2 * 5 * 3 = -15/30 = -1/2 и, следовательно, C = 120º.

Теперь, если вы можете применить закон груди и получить 5 / sin (A) = 3 / sin (B) = 7 / sin (120), где вы можете очистить B и получить это без (B) = 3 * грех (120º) / 7 = 0,371, так что B = 21,79º.

Наконец, последний угол рассчитывается с использованием A = 180º-120º-21,79º = 38,21º..