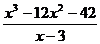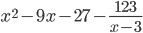Как решать деление треугольником (3 видео)

Деление многочлена на многочлен «уголком»

В этой статье рассмотрим один из способов разложения на множители многочленов высших степеней. С его помощью вы сможете решать уравнения и неравенства вида:

Пример:
(6x^2+6+x^3+11x) записываем как (x^3+6x^2+11x+6)

1) Подбором найдите один из корней многочлена.

Для этого вместо (x) подставьте по очереди числа: (±1,±2,±3,±4,±5) и т.д. Число, которое сделает многочлен нулем и будет его корнем.

Пример:
(x^3+6x^2+11x+6)
Подставим (1). Имеем: (1^3+6 cdot 1^2+11cdot 1+6=24) — не равно нулю. Ищем дальше.
Подставим (-1). Получим: ((-1)^3+6cdot (-1)^2+11cdot (-1)+6=-1+6-11+6=0) – значит (-1) корень нашего многочлена.

Матхак! Пробуйте сначала числа, на которые свободный член делиться нацело. В данном случае свободный член (6), поэтому в первую очередь нужно пробовать числа: (±1,±2,±3) и (±6).

2) Поделите исходный многочлен на (x-x_0), где (x_0) – найденный корень. Процесс деления многочлена на многочлен сильно похож на обычное деление в столбик — поэтому и называется деление «уголком».

а) Запишите многочлены как числа при делении столбиком:

б) Подберите такой одночлен, чтобы при умножении его на (x), получалось первое слагаемое исходного многочлена, то есть в нашем случае (x^3). Очевидно, что таким одночленом будет (x^2).

в) Умножьте этот одночлен на делитель и запишите результат под исходным многочленом. Таким образом, мы умножаем (x^2) на (x+1) и получаем (x^3+x^2).

г) Теперь точно так же, как в случае деления натуральных чисел, поставьте знак минус, проведите горизонтальную черту и сделайте вычитание.

д) Повторите шаги б) – г) только уже с новым многочленом:
— подберите такой одночлен, чтобы при умножении на (x) первое слагаемое было таким же, как в новом многочлене: в нашем примере этим одночленом будет (5x).
— умножьте этот одночлен на делитель: умножив (5x) на (x+1) получим (5x^2+5x).
— вычтите получившиеся многочлены:

е) И вновь повторяем шаги б) – г) до тех пор, пока после вычитания не останется ноль.

3) Запишите новый вид многочлена, представив его как произведение делителя и частного.
(x^3+6x^2+11x+6=(x+1)(x^2+5x+6))

Матхак! Если есть сомнения в правильности разложения, можно проверить его раскрытием скобок – в результате должен получиться исходный многочлен.
Проверим наш случай: ((x+1)(x^2+5x+6)=x^3+5x^2+6x+x^2+5x+6=x^3+6x^2+11x+6).
Получен исходный многочлен, значит, поделили правильно.

Матхак! Если в результате деления у вас в остатке получился не ноль, значит, скорее всего, в решении есть ошибка.

Давайте теперь решим пример с применением изученного материала.

Пример: Решите неравенство (x^4-3x^3+6x-4≥0).

Найдем один из корней многочлена слева. Проверим (1).

Поделим многочлен (x^4-3x^3+6x-4) на ((x-1)) уголком. Однако замечаем, что у нас нет слагаемого с квадратом. Чтоб нам было удобнее решать, запишем вместо него выражение (0·x^2) (ведь его значение равно нулю, а значит оно ничего не меняет в исходном многочлене).

Запишем новый вид нашего неравенства.

С первой скобкой все хорошо, а вот вторую надо бы разложить еще. Так как высшая степень в ней — куб, то мы можем попробовать разложить методом группировки, что проще чем деление в столбик. У первых двух слагаемых вынесем за скобку (x^2), а у третьего и четвертого – минус двойку.

Теперь выносим общую скобку ((x-2)) за скобку.

Но и это еще не все, потому что (x^2-2) можно разложить с помощью формулы сокращенного умножения «разность квадратов»: (a^2-b^2=(a-b)(a+b)).

Вот сейчас все готово для применения метода интервалов .

Содержание

Деление в столбик
Как правильно делить в столбик
Как выглядит деление в столбик с остатком
Примеры на деление в столбик
Деление многочленов столбиком
💥 Видео

Видео:Как делить уголком? Деление столбикомСкачать

Деление в столбик

О чем эта статья:

3 класс, 4 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Как объяснить деление в столбик? Деление чисел уголком. Деление на многозначного на однозначное.Скачать

Как правильно делить в столбик

Делить столбиком проще, чем высчитывать в уме. Этот способ наглядный, помогает держать во внимании каждый шаг и запомнить алгоритм, который впоследствии будет срабатывать автоматически.

Рассмотрим пример деления трехзначного числа на однозначное 322 : 7. Для начала определимся с терминами:

322 — делимое или то, что необходимо поделить;
7 — делитель или то, на что нужно поделить:
частное — результат действия.

Шаг 1. Слева размещаем делимое 322, справа делитель 7, между ставим уголок, а частное посчитаем и запишем под делителем.

Шаг 2. Смотрим на делимое слева направо и находим ту часть, которая больше делителя. 3, 32 или 322? Нам подходит 32. Теперь нужно определить сколько раз наш делитель 7 содержится в числе 32. Похоже, что четыре раза.

Проверяем: 4 × 7 = 28, а 28

Шаг 3. Остаток равен 4. Для продолжения решения его нужно увеличить. Мы сделаем это за счет следующей цифры делимого. Приписываем к четверке оставшуюся двойку и продолжаем размышлять.

Шаг 4. Сколько раз делитель 7 содержится в числе 42? Кажется, шесть раз. Проверяем: 7 × 6 = 42, 42 = 42 — все верно. Записываем полученное число к четверке справа — это вторая цифра частного. Делаем вычитание в столбик 42 из 42, в остатке получаем 0. Значит, числа разделились нацело.

Мы закончили решать пример и в результате получили целое число 46.

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Как выглядит деление в столбик с остатком

Это такое же деление, только в результате получается неровное число, как получилось в примере выше.

Например, делим 19 на 5. Наибольшее число, делящееся на 5 до 19 это 15. Проверяем 5*3=15, 19-15=4. Ответ: 3 и остаток 4. Записываем так: 19:5=3(4).
Еще пример: делим 29 на 6. Также определяем максимальное число, делящееся на 6 до 29. Подходит 24. Ответом будет: 4 и остаток 5. А записываем: 29:6=4(5).

Видео:Преобразование звезды сопротивлений в эквивалентный треугольник. Преобразование мостовой схемыСкачать

Примеры на деление в столбик

Давайте закрепим знания на практике. Для этого разделите столбиком примеры ниже, а после проверьте полученные цифры — чур, не подглядывать!

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Деление многочленов столбиком

Алгоритм деления в столбик применяется в частности при нахождении интегралов.

Решение онлайн
Видеоинструкция

Пример деления в столбик . Найти частное деления и остаток многочлена:

№1.

x 3 -12x 2 -42	x -3
x 3 -3x 2	x 2
-9x 2 -42

№2.

x 3 -12x 2 -42	x -3
x 3 -3x 2	x 2 -9x
-9x 2 -42
-9x 2 + 27x
-27x -42

№3.

x 3 -12x 2 -42	x -3
x 3 -3x 2	x 2 -9x -27
-9x 2 -42
-9x 2 + 27x
-27x -42
-27x + 81
-123

Целая часть: x 2 -9x -27
Остаток: -123

Таким образом, ответ можно записать как:
см. также и другие примеры решение столбиком.

Пример №1 . Найти частное и остаток от деления многочлена на многочлен:
P(x)=2x 5 +3x 3 -x 2 +4x+1, Q(x)=2x 2 -x+1

Пример №2 . Не производя деление найти остаток от деления многочлена на двучлен:
P(x)=-x 4 +6x 3 -2x 2 +x-2, Q(x)=x-6
Решение. Выделим общий множитель (x-6).
-x 3 (x-6)-2x(x-6)-12x+x-2 = -x 3 (x-6)-2x(x-6)-11(x-6)-66-2 = -x 3 (x-6)-2x(x-6)-11(x-6)-68
Остаток от деления: -68/(x-6)