Как превратить треугольник в квадрат (7 видео)

Разрезание Дьюдени — неразрывная цепочка разрезания

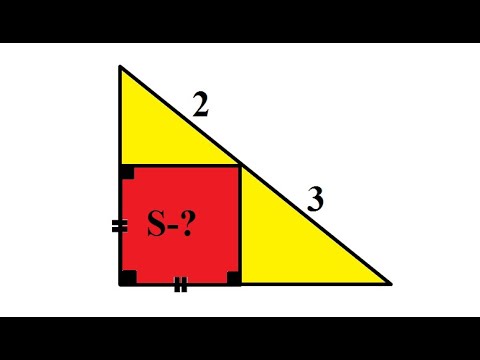
Можно ли разрезать треугольник на такое количество частей, чтобы из них можно было сложить квадрат?

Утвердительный ответ на этот вопрос был дан еще в 1807 году. В более общем виде это звучало так: «Любые два многоугольника общей площади должны иметь общее разрезание». Это теорема Бойля –Гервина, доказанная в 1807. Е сли у нас есть треугольник и квадрат и мы знаем, что их площади одинаковы, разрезав треугольник на несколько многоугольников, мы можем как из мозаики сложить квадрат.

Но вот более сложный вопрос. А можно ли разрезать так, чтобы все части оставались соединенными в неразрывную цепочку?

Шарнирное разрезание или разрезания Дью-дени (по имени автора), выполненное в виде анимации, демонстрирует нам как треугольник преобразуется в квадрат, а затем в шестиугольник и обратно в треугольник (использован анимационный ролик из Wikipedia).

Содержание

Изначально задача о разрезании треугольника была предложена Генри Дьюдени в виде головоломки и опубликована в газете «Дейли мейл» (выпуски от 1 и 8 февраля 1905 г.). Позже эта головоломка вошла в книгу «Кентерберийские головоломки» и по сей день входит в сотню лучших головоломок «всех времен».
Как из 3 треугольников сделать квадрат
Творим, фантазируем, сочиняем из геометрических фигур
💡 Видео

Видео:Треугольники в четырехугольники в BlenderСкачать

Изначально задача о разрезании треугольника была предложена Генри Дьюдени в виде головоломки и опубликована в газете «Дейли мейл» (выпуски от 1 и 8 февраля 1905 г.). Позже эта головоломка вошла в книгу «Кентерберийские головоломки» и по сей день входит в сотню лучших головоломок «всех времен».

В переведенном издании (Дьюдени Г. Э. Кентерберийские головоломки / Перевод с английского Ю. Н. Сударева. — М.: Мир, 1979. — С. 46—47.) исходный текст звучит следующим образом:

Видео:Как двумя шарами превратить треугольник в квадрат?Скачать

Как из 3 треугольников сделать квадрат

Методы быстрого лоскутного шитья существенно облегчают и ускоряют работу мастерицы. За многие годы рукодельницы придумали огромно количество различных способов упростить себе работу. О самых популярных мы и расскажем.

Квадраты из треугольников.

В англо-американской школе квилтинга все измерения производятся в дюймах ( 2,5 см ). Если если квадрата — это целая единица блока, то треугольники в квилтинге делятся на половинки — половина квадрата (half square triangles), и четвертинки — четверть целого квадрата (quarter square triangles) . Различие есть в направлении долевой нити. Поэтому некоторые треугольники выкраиваются по два треугольника в квадрата, а другие — по четыре треугольника.

При использовании быстрого метода шитья квадрата из треугольников важно правильно рассчитать размер заготовки и припуски .

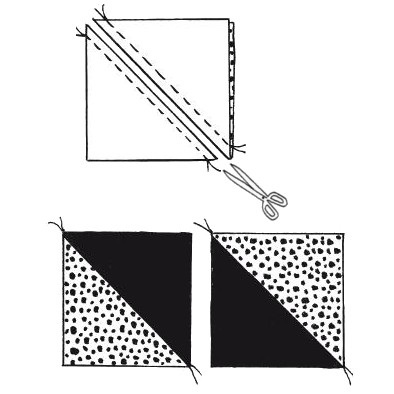
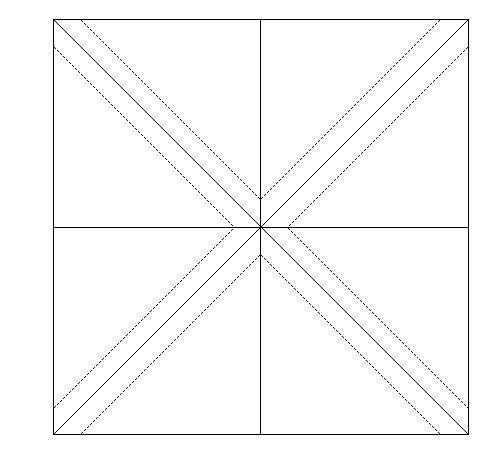
Квадрат из двух треугольников (half square triangles) :
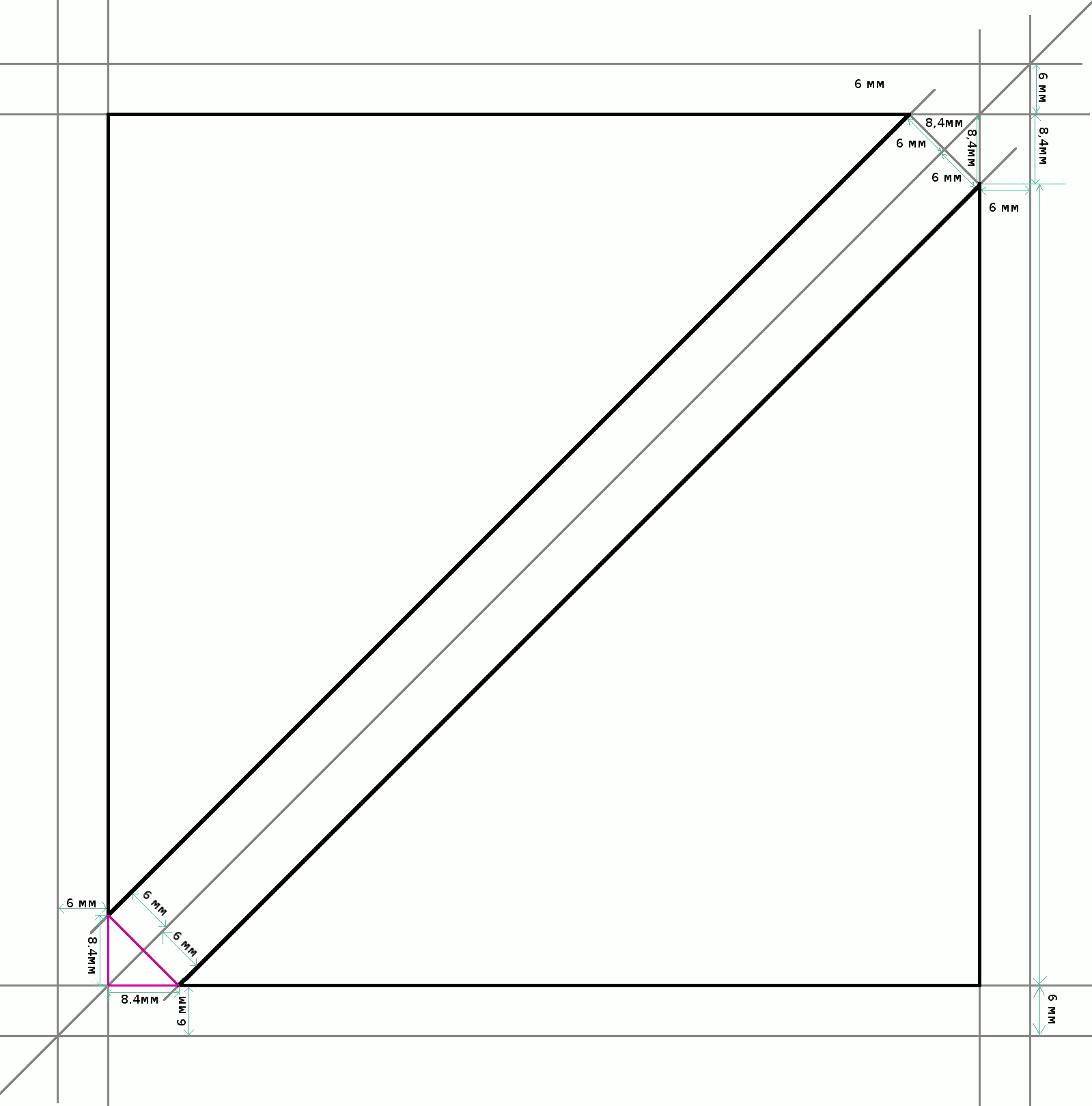
выкроите квадрат размером, равным стороне треугольника + 2 припуска на шов в 6мм + припуск на диагональный шов 8,4 мм. Величина дополнительного припуска не зависит от размера треугольников и квадратов, она зависит от величины припуска. Если Вы привыкли использовать другой припуск : 7мм или 5 мм , то величина дополнительного припуски рассчитывается по формуле : (припуск х припуск) , вычислить квадратный корень из результата и разделить его на 2. (Обоснование: поскольку по формуле Пифагора квадрат гипотенузы равен сумма квадратов катетов, а в данном случае гипотенуза — это два припуска, то катет — это дополнительный припуск, мы берем гипотенузу, извлекаем из нее квадратный корень и делим на два ).

Пример: Вам нужны 2 детали из двух треугольников — квадрат — размером 5х5см . Вы используете припуски 6 мм ( 0,6 см )
Выкроите два квадрата размером 7 х 7 см ( 5 +0,6 + 0,6 + 0,84) . Сложите их лицевыми сторонами. Для удобства можно обозначить диагональ, вдоль которой вы будете прокладывать строчки, маркером или мелом. Проложите две строчки вдоль диагонали ( на расстоянии 6 мм от диагонали). Сделайте разрез по диагонали, между строчками . Разверните детали и заутюжьте припуски.

Если Вам необходимо больше двух составных квадратов , можно на разрезать ткань на квадраты, а использовать полоску шириной в несколько квадратов или большой квадрат (см схему ниже) .

Квадрат из четырех треугольников (quarter square triangles):
выкроите квадрат размером, равным гипотенузе (длинной) треугольника + 2 припуска на шов в 6мм + 2 припуска на диагональный шов 8,4 мм.
Пример: Вам нужны 2 детали из четырех треугольников — квадрат размером 10 х 10 см (и припуском 0,6см). (см. схему сборки ниже) Нужно выкроить два квадрата размером 10 + (0,6 * 2) + (0,84 * 2) = 12,9 см , т.е. 12,9 х 12,9 см. Сложите квадраты лицевыми сторонами, обозначьте диагонали и линии швов. Прострочите линии швов вдоль одной диагонали. Разрежьте по этой диагонали квадраты пополам. Разверните детали и отутюжьте.
Снова сложите получившиеся квадраты лицевыми сторонами, совмещая линии швов. Прострочите линии швов вдоль второй диагонали. Разрежьте по этой диагонали квадраты пополам. Разверните детали и отутюжьте.
Получилось два квадрата из 4-х треугольников каждый.

Быстрые треугольники — полквадрата . Быстрый метод сборки треугольников в квадраты.

Схема выкройки квадрата для данного метода .

Выкроите квадраты двух цветов. Сложите их лицевыми сторонами. Проложите две строчки вдоль диагонали ( на расстоянии 6 мм от диагонали).

Сделайте разрез по диагонали. Разверните детали и заутюжте припуски

Квадрат из двух треугольников — несколько квадратов в ряд .

Квадрат из четырех треугольников (quarter square triangles): четверть-квадрат Обратите внимание, здесь долевая нить проходит вдоль диагонали будущего квадрата (вдоль гипотенузы треугольника)

Выкроите квадрат. Прострочите швы вдоль сторон квадрата — отмечено красным. Разрежьте квадрат по диагоналям. Раскройте и заутюжьте детали.

Получаются квадраты с долевой нить вдоль диагонали квадрата.

В той же самой выкройке, проложив шов по синим , или по зеленым линиям, и разрезав квадрат по диагоналям, Вы получите составные треугольники из четверть-квадратов с долевой по короткой стороне (катету) треугольника.

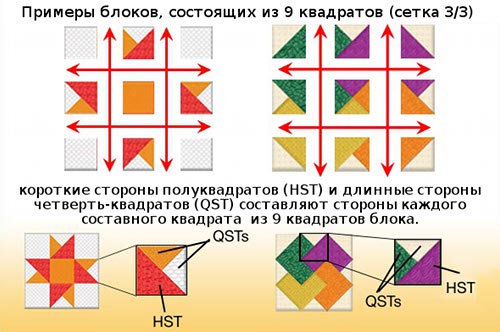
Пример сборки блоков 3/3 квадрата из полу-квадратов и четверть-квадратов.

Квадраты из 4-х треугольников (четверть-квадратов).

Выкроите квадраты, сложите, обозначьте линии швов и линии разреза. Прострочите. Разрежьте.

Разутюжьте детали. Сложите их лицевыми сторонами, совмещая линии швов. Обозначьте линии швов и линии разреза. Прострочите. Разрежьте.

Получилось два квадрата с бантиками (квадрат из четверть-квадратов).

Я же хочу представить другой плоский геометрический конструктор, который можно назвать«Пифагор-2».

Квадрат размером 10х10 см разрезается, так как показано на рисунке, в результате чего получаем 9 геометрических фигур: 4 больших треугольника, 2 маленьких, один средний, квадрат и прямоугольник.

Перед тем как работать с образцами, ребята выполняют несколько заданий с определенными фигурами.

Задание 1.
Возьмите 2 больших треугольника и квадрат. Сделайте: прямоугольник, треугольник и 2 разных четырехугольника, один из которых – трапеция.

Задание 2.
Возьмите 2 маленьких треугольника и средний. Сделайте: квадрат, треугольник, прямоугольник и 2 разных четырехугольника, один из которых – трапеция.

Задание 3.
Возьмите 2 маленьких треугольника, средний и большой треугольник. Сделайте: квадрат, треугольник, прямоугольник и 2 разных четырехугольника, один из которых – трапеция.

Далее дети строят разные образы, постепенно переходя к нерасчлененным образцам.

Следующий конструктор тоже авторского исполнения и по аналогии с «Танграмом» я его назвал«Треграм», так как получен путем разрезания равностороннего треугольника. Игровые задания с таким конструктором можно проводить на заполнение и составление плоскостных изображений из наборов геометрических фигур. Равносторонний треугольник из картона (длина стороны 20 см, каждая из которых поделена на 5 равных частей по 4 см) разрезается на 10 фигур, как показано на рисунке.

В итоге получается 4 маленьких треугольника, 2 ромба, трапеция, параллелограмм, большой треугольник и шестиугольник.

Вся работа также строится поэтапно.

На первом этапе дети знакомятся со всеми частями конструктора, составляя их из треугольников и других маленьких фигур:

1. Присоединив друг к другу два треугольника, дети получают ромб.
2. Присоединив к ромбу ещё один треугольник, дети получают трапецию, которую можно сделать и с помощью трёх треугольников.
3. Присоединив к трапеции ещё один треугольник, дети получают параллелограмм. Эту же фигуру можно составить и из других маленьких фигур.
4. Далее дети путём наложения маленьких фигур на большие сами делают выводы, из каких фигур их можно сложить.

На втором этапе дети заполняют внутреннее пространство фигур-силуэтов на листах, используя все части конструктора.

На третьем этапе дети составляют плоскостные изображения по расчленённым образцам с постепенным переходом к частично расчленённым.

На четвёртом этапе дети моделируют изображения по собственному замыслу.

По типу «Никитинских кубиков», я сделал ещё один плоский конструктор. Этот набор состоит из 15 квадратов 5х5 см:

· 8 квадратов закрашены наполовину по диагонали;

· 3 квадрата закрашены полностью;

· 4 квадрата чисто белые.

На первом этапе игровых заданий мы используем только 4 квадрата, закрашенных наполовину, и по образцу все изображения составляем только из них.

На втором этапе дети составляют изображения из 9 квадратов, используя весь набор.

Цель. Учить детей составлять геометрические фигуры из определенного количества палочек, пользуясь приемом пристроения к одной фигуре, взятой за основу, другой.

Материал: У детей на столах счетные палочки, доска, мел на данном и следующем занятиях.

Ход работы. 1. Воспитатель предлагает детям отсчитать по 5 палочек, проверить и положить их перед собой. Затем говорит: «Скажите, сколько потребуется палочек, чтобы составить треугольник, каждая сторона которого будет равна одной палочке. Сколько потребуется палочек для составления двух таких треугольников? У вас только 5 палочек, но из них надо составить тоже 2 равных треугольника. Подумайте, как это можно сделать, и составляйте».

После того как большинство детей выполнят задание, воспитатель просит их рассказать, как надо составить 2 равных треугольника из 5 палочек. Обращает внимание ребят на то, что выполнять задание можно по-разному. Способы выполнения надо зарисовать. При объяснении пользоваться выражением «пристроил к одному треугольнику другой снизу» (слева и т.д.), а в объяснении решения задачи пользоваться также выражением «пристроил к одному треугольнику другой, используя лишь 2 палочки».

2. Составить 2 равных квадрата из 7 палочек (воспитатель предварительно уточняет, какую геометрическую фигуру можно составить из 4 палочек). Дает задание: отсчитать 7 палочек и подумать, как из них составить на столе 2 равных квадрата.

После выполнения задания рассматривают разные способы пристроения к одному квадрату другого, воспитатель зарисовывает их на доске.

Вопросы для анализа: «Как составил 2 равных квадрата из 7 палочек? Что сделал сначала, что потом? Из скольких палочек составил 1 квадрат? Из скольких палочек пристроил к нему второй квадрат? Сколько потребовалось палочек для составления 2 равных квадратов?»

Цель. Составлять фигуры путем пристроения. Видеть и показывать при этом новую, полученную в результате составления фигуру; пользоваться выражением: «пристроил к одной фигуре другую», обдумывать практические действия.

Ход работы. Воспитатель предлагает детям вспомнить, какие фигуры они составляли, пользуясь приемом пристроения. Сообщает, чем они сегодня будут заниматься — учиться составлять новые, более сложные фигуры. Дает задания:

1. Отсчитать 7 палочек и подумать, как можно из них составить 3 равных треугольника.

После выполнения задания воспитатель предлагает всем детям составить 3 треугольника в ряд так, чтобы получилась новая фигура — четырехугольник (рис. 2). Этот вариант решения дети зарисовывают мелом на доске. Воспитатель просит показать 3 отдельных треугольника, четырехугольник и треугольник (2 фигуры), четырехугольник.

Рис. 2 Составление фигур из треугольников

2. Из 9 палочек составить 4 равных треугольника. Подумать, как это можно сделать, рассказать, затем выполнять задание.

После этого воспитатель предлагает детям нарисовать мелом на доске составленные фигуры и рассказать о последовательности выполнения задания.

Вопросы для анализа: «Как составил 4 равных треугольника из 9 палочек? Какой из треугольников составил первым? Какие фигуры получились в результате и сколько?»

Воспитатель, уточняя ответы детей, говорит: «Начинать составлять фигуру можно с любого треугольника, а потом к нему пристраивать другие справа или слева, сверху или снизу».

Цель. Упражнять детей в самостоятельных поисках путей составления фигур на основе предварительного обдумывания хода решения.

Ход работы. Воспитатель задает детям вопросы: «Из скольких палочек можно составить квадрат, каждая из сторон которого равна одной палочке? 2 квадрата? (из 8 и 7). Как будете составлять 2 квадрата из 7 палочек?»

1. Отсчитать 10 палочек и составить из них 3 равных квадрата. Подумать, как надо составлять, и рассказать.

По мере выполнения воспитатель вызывает нескольких детей зарисовать составленные ими фигуры на доске и рассказать последовательность составления. Предлагает всем детям составить фигуру из 3 равных квадратов, расположенных в ряд, по горизонтали. На доске рисует такую же и говорит: «Посмотрите на доску. Здесь нарисовано, как можно по-разному решать эту задачу. Можно пристраивать к одному квадрату другой, а затем и третий. (Показывает.) А можно составить прямоугольник из 8 палочек, затем разделить его на 3 равных квадрата 2 палочками». (Показывает.) Затем задает вопросы: «Какие фигуры получились и сколько? Сколько прямоугольников получилось? Найдите и покажите их».

2. Из 5 палочек составить квадрат и 2 равных треугольника. Сначала рассказать, а затем составлять.

При выполнении этого задания дети, как правило, допускают ошибку: составляют 2 треугольника усвоенным способом — пристроением, в результате чего получается четырехугольник. Поэтому воспитатель обращает внимание ребят на условие задачи, необходимость составления квадрата, предлагает наводящие вопросы: «Сколько палочек нужно для составления квадрата? Поскольку у вас палочек? Можно ли составить, пристраивая 1 треугольник к другому? Как составить? С какой фигуры надо начинать составлять?» После выполнения задания дети объясняют, как они делали: надо составить квадрат и разделить его 1 палочкой на 2 равных треугольника.

Цель. Упражнять детей в умении высказывать предположительное решение, догадываться.

Ход работы. 1. Из 9 палочек составить квадрат и 4 треугольника. Подумать и сказать, как надо составлять. (Несколько детей высказывают предположения.)

Если дети затрудняются, воспитатель советует: «Вспомните, как составляли из 5 палочек квадрат и 2 треугольника. Подумайте и догадайтесь, как можно выполнить задание. Тот, кто первым решит задачу, зарисует полученную фигуру на доске».

После выполнения и зарисовки ответа воспитатель предлагает всем детям составить у себя одинаковые фигуры (рис. 3).

Рис. 3 Составление фигур из треугольников

Вопросы для анализа: «Какие геометрические фигуры получились? Сколько треугольников, квадратов, четырехугольников? Как составляли? Как удобнее, быстрее составлять?»

2. Из 10 палочек составить 2 квадрата — маленький и большой.

3. Из 9 палочек составить 5 треугольников.

При необходимости в ходе выполнения второго и третьего заданий воспитатель дает наводящие вопросы, советы: «Сначала подумайте, затем составьте. Не повторяйте ошибок, ищите новый ход решения. Говорится ли в задаче о размере треугольников? Это задачи на смекалку, надо сообразить, догадаться, как решить задачу».

Итак, в начальный период обучения детей 5 лет решению простых задач на смекалку они самостоятельно, в основном практически действуя с палочками, ищут путь решения. С целью развития у них умения планировать ход мысли следует предлагать детям высказывать предварительные рассуждения или сочетать их с практическими пробами, объяснять способ и путь решения.

Возможно несколько видов решения задач первой группы. Усвоив способ пристроения фигур при условии общности сторон, дети очень легко и быстро дают 2-3 варианта решения. Каждая фигура при этом отличается от прежней пространственным положением. Одновременно дети осваивают способ построения заданных фигур путем деления полученной геометрической фигуры на несколько (четырехугольник или квадрат на 2 треугольника, прямоугольник — на 3 квадрата).

Решение с детьми 5-6 лет более сложных задач на перестроение фигур следует начинать с тех, в которых с целью изменения фигуры надо убрать определенное количество палочек и наиболее простых — на перекладывание палочек.

Процесс поисков детьми решения задач второй и третьей групп гораздо сложнее, нежели первой группы. Для этого нужно запомнить и осмыслить характер преобразования и результат (какие фигуры должны получиться и сколько) и постоянно в ходе поисков решения соотносить его с предполагаемыми или уже осуществленными изменениями. В процессе решения необходим зрительный и мыслительный анализ задачи, умение представить возможные изменения в фигуре.

Таким образом, в процессе решения задач дети должны овладеть такими мыслительными операциями анализа задачи, в результате которых можно представить мысленно различные преобразования, проверить их, затем, отбросив неверные, искать и пробовать новые ходы решения. Обучение должно быть направлено на формирование у детей умения обдумывать ходы мысленно, полностью или частично решать задачу в уме, ограничивать практические пробы.

В какой последовательности надо предлагать детям 5-6 лет задачи на смекалку второй и третьей групп?

В фигуре, состоящей из 5 квадратов, убрать 4 палочки, оставив один прямоугольник (рис. 4).

Рис. 4

В фигуре, состоящей из 6 квадратов, убрать 2 палочки, чтобы осталось 4 равных квадрата (рис. 5).

Рис. 5

Составить домик из 6 палочек, а затем переложить 2 палочки так, чтобы получился флажок (рис. 6).

Рис. 6

В данной фигуре переложить 2 палочки, чтобы получилось 3, равных треугольника (рис. 7).

Рис. 7

В фигуре, состоящей из 5 квадратов, убрать 3 палочки, чтобы осталось 3 таких же квадрата (рис. 8).

Рис. 8

В фигуре, состоящей из 4 квадратов, убрать 2 палочки, чтобы осталось 2 неравных квадрата (рис. 9).

Рис. 9

В фигуре из 5 квадратов убрать 4 палочки, чтобы осталось 2 неравных квадрата (рис. 10).

Рис. 10

В фигуре из 5 квадратов убрать 4 палочки, чтобы остались 3 квадрата (рис. 11).

Рис. 11

В фигуре из 4 квадратов переложить 2 палочки так, чтобы получилось 5 квадратов (рис. 12).

Рис. 12

В фигуре из 5 квадратов убрать 4 палочки, чтобы осталось 3 квадрата (рис. 13).

Рис. 13

Для этих и других аналогичных задач на смекалку характерно то, что преобразование, необходимое для решения, ведет к изменению количества квадратов, из которых составлена заданная фигура (задачи 2, 5 и др.), изменению их размера (задачи 6, 7), видоизменению фигур, например преобразование квадратов в прямоугольник в задаче 1.

В ходе занятий с целью руководства поисковой деятельностью детей воспитатель пользуется различными приемами, способствующими воспитанию у них положительного отношения к длительному настойчивому поиску, но в то же время быстроты реакции, отказа от выработанного пути поисков. Интерес детей поддерживается желанием достичь успеха, для чего нужна активная работа мысли.

Видео:Преобразование звезды сопротивлений в эквивалентный треугольник. Преобразование мостовой схемыСкачать

Творим, фантазируем, сочиняем из геометрических фигур

Творим, фантазируем, сочиняем

из геометрических фигур?

Задумались ли вы о том, что все можно изобразить с помощью геометрических фигур! Существует очень много игр для развития воображения детей. Во что же можно превратить геометрическую фигуру? Геометрические формы встречаются нам повсюду, их можно разглядеть в большинстве окружающих нас предметов: мяч круглый, стол прямоугольный и т. д. Анализируя сходство окружающих предметов с геометрическими фигурами, ребенок замечательно тренирует ассоциативное и пространственное мышление.

Изучение геометрических фигур полезно для общего развития ребенка, расширения его знаний об окружающем мире. Если знакомить ребенка с формами в раннем возрасте, в школе ему придется гораздо проще. На умении отличать геометрические фигуры основано множество интересных развивающих игр. Итак, игры для изучения и закрепления знаний о геометрических фигурах:

1. Называем геометрические фигуры всегда и везде

Если во время игр или чтения книг вам встречается какая-либо фигура, обязательно обращайте на нее внимание ребенка и называйте ее («Посмотри, мячик похож на круг, а кубик на квадрат»). Даже если вам кажется, что ребенок еще вряд ли запомнит названия фигур, все равно произносите их, и они обязательно отложатся у него в голове. Делать это можно уже до года. Поначалу указывайте только на основные фигуры (квадрат, круг, треугольник), затем, когда поймете, что ребенок их усвоил, начинайте изучать и другие фигуры.

2. Играем в геометрическое лото. При помощи лото можно изучать все, что угодно: цвета, геометрические фигуры, овощи, животных и т. д.

А геометрическое лото к тому же довольно легко сделать самостоятельно: на листе бумаги или картона рисуем или распечатываем два одинаковых набора фигур, один из которых разрезаем на карточки. Все готово, можно играть.

3. Рисуем геометрические фигуры. Во время совместного рисования с ребенком также не забывайте произносить названия форм. «Так, нарисуем квадрат, теперь треугольник — получился домик» и т. д.

Таким образом, ребенок не только запомнит изодражения фигур, то и из каких реометрических фигур можно представить изображаемый объект.

Использовать геометрические фигуры в занятиях по аппликации можно хоть с самого первого занятия.

Аппликации из геометрических фигур – это забавное, интересное и полезное занятие.

С помощью аппликаций у детей развиваются творческие способности, внимание, память, логика, фантазия, мелкая моторика.

Маленьким деткам такие аппликации нужно делать вместе с взрослыми, поскольку нужно заготовить все элементы и вырезать их. Помогая родителям делать аппликации, малыши лучше запоминают геометрические фигуры, цвета, изучают животных и окружающий мир.

Дайте возможность ребеночку подобрать соответствующие геометрические фигуры и приклеить их на нужное место. Когда у него получится какое-то животное, он будет очень рад. Аппликации можно делать из цветной бумаги, а можно из однотонной, а потом разрисовать.

Игры на превращение фигур в формы и изображения.