Как построить треугольник схема

Задачи на построение

Широкое распространение в геометрии получили задачи на построение. Суть этих задач состоит в следующем: при заданных начальных условиях нужно построить тот или иной геометрический объект при помощи линейки и циркуля. Разберем общие принципы решения данных задач:

Анализирование задачи. На этом этапе необходимо установить взаимосвязь между заданными условиями и объектом, который нужно изобразить. Результатом выполнения этого этапа является план решения задачи.

Построение. Согласно разработанного плана выполняется построение объекта.

Доказательство. На этом этапе необходимо доказать, что изображенная фигура полностью соответствует заданным условиям.

Сложно разобраться самому?

Попробуй обратиться за помощью к преподавателям

Изучение. На этом этапе выполняется анализ начальных условий и определение, при каких условиях задача решается одним способом, при каких двумя, а при каких – вовсе не решаема.

Разберем задачи на построение треугольника по трем различным начальным условиям.

Изображение треугольника, если задана одна сторона и два прилегающих к ней угла

Задана одна сторон треугольника (BC) и прилежащие к ней углы (∝) и (β) , необходимо построить треугольник.

1. Анализируем условия. Необходимо построить треугольник (ABC) , имея одну сторону (BC) и углы (∠K= ∝ и ∠M= β) к ней прилежащие. Разработаем план решения задачи:

• Начертим прямую a, а на ней отмерим отрезок (BC) ;
• Изображаем угол (∠K= ∝) с центром в вершине (B) на стороне (BC) ;
• Изображаем угол (∠M= β) с центром в вершине (C) на стороне (BC) ;
• На пересечении лучей построенных углов получим точку (A) , соединяем ее с точками (C) и (B) , получаем отрезки (AC) и (AB) .

2. Строим треугольник

3. Доказательство. По изображенному рисунку делаем вывод, что все заданные условия выполнены в полной мере.

4. Изучение. Заданные углы могут быть построены и в противоположную сторону, соответственно мы можем построить еще один треугольник, но так как он точно такой же, как и первый, можно считать, что решение этой задачи единственное. Учитывая то, что сумма всех углов треугольника должна равняться 180 0 , если сумма углов (∝) и (β) будет равна или больше 180 0 , решения задача не будет иметь.

Изображение треугольника, если заданы три стороны

Заданы три стороны треугольника (AB) , (AC) и (BC) , нужно построить треугольник.

1. Анализируем условия. Необходимо построить треугольник (ABC) , имея три стороны (AB) , (AC) и BC. Разработаем план решения задачи:

• Начертим прямую (a) , а на ней отмерим отрезок (AB) ;
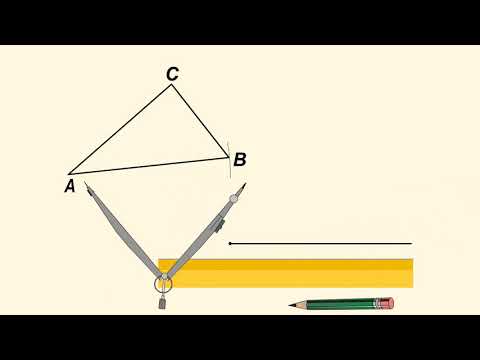
• Чертим с помощью циркуля две окружности. Одна окружность будет с центром в точке (A) с радиусом (AC) , а вторая с центром в точке (B) с радиусом (BC) ;
• На пересечении окружностей мы получим точку (C) , соединяем ее с точками (A) и (B) , получаем отрезки (AC) и (BC) .

2. Строим треугольник:

3. Доказательство. По изображенному рисунку делаем вывод, что все заданные условия выполнены в полной мере.

Не нашли что искали?

Просто напиши и мы поможем

4. Изучение. Построенные окружности имеют две точки пересечения, поэтому мы можем построить еще один треугольник, но так как он точно такой же, как и первый, можно считать, что решение этой задачи единственное. Учитывая то, что сумма двух сторон треугольника всегда больше, чем третья его сторона, можно сделать вывод, если это условие не будет выполнено для заданных сторон, то задача не будет иметь решение.

Изображение треугольника, если заданы две стороны и угол между ними

Заданы две стороны треугольника (AB) и (AC) , а также угол ∝ между ними, необходимо построить треугольник.

1. Анализируем условия. Необходимо построить треугольник (ABC) , имея стороны (AB) и (AC) , а также угол (CAB) , равный (∝) . Разработаем план решения задачи:

• начертим прямую (a) , а на ней отмерим отрезок (AB) ;
• отмеряем угол (MAB) , равный (∝) ;
• откладываем отрезок (AC) на прямой (AM) ;
• чертим третью сторону треугольника (CB) , соединяя точки (B) и (C) .

2. Строим треугольник:

3. Доказательство. По изображенному рисунку делаем вывод, что все заданные условия выполнены в полной мере.

4.Изучение. Прямая a бесконечна, поэтому таких треугольников можно изобразить очень много, но учитывая тот факт, что они все одинаковые, будем считать, что задача имеет одно решение. При условии, если угол (∝) будет равен или больше 180 0 , решения задача не будет иметь, так как сумма всех углов треугольника должна равняться 180 0 .

Геометрия. 7 класс

Конспект урока

Построение треугольника по трём элементам

Перечень вопросов, рассматриваемых в теме:

• Задачи на построение циркулем и линейкой.
• Алгоритмы решения простейших задач на построение.
• Способы решения задач на построение треугольника по трём заданным элементам.
• Этапы решения задач на построение: анализ, построение, доказательство, исследование.

Задачей на построение называется предложение, указывающее, по каким данным, какую геометрическую фигуру требуется построить, чтобы эта фигура удовлетворяла определённым условиям.

Построение треугольника по трём элементам:

• по 2 сторонам и углу между ними;
• по стороне и двум прилежащим к нему углам;
• по трём сторонам.

Задачи на построение:

• позволяют моделировать те или иные практические ситуации
• устанавливают связь между геометрией и черчением, геометрией и рисованием.

1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

1. Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
2. Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
3. Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
4. Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
5. Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения

Построение треугольника по трём элементам.

Чтобы построить треугольник, нужно уметь строить:

1. Отрезок, равный данному.

2. Угол, равный данному.

Любая задача на построение включает в себя четыре основных этапа.

Анализ: предположить, что задача решена, сделать чертеж от руки искомой фигуры, составить план решения задачи.

Построение: описать способ построения.

Доказательство: доказать, что построенная фигура или множество точек – искомые.

Исследование: выяснить, всегда ли построение возможно.

Построить треугольник по трём заданным сторонам.

Построить треугольник по двум сторонам и углу между ними.

Построить треугольник по стороне и двум прилежащим к ней углам.

Разбор решения заданий тренировочного модуля.

Задача 1. Найдите расстояние от вершины В до прямой АС.

Дано. В треугольнике АВС: АВ = ВС = 10 см, ∠АВС = 120°.

∆АВС – равнобедренный. ВН – расстояние от точки В до прямой АС, т. е. ВН ⊥ АС. В равнобедренном треугольнике высота является биссектрисой. ∠АВН = 120°: 2 =60°, значит, ∠А = 30°. Против угла 30° лежит катет ВН равный половине гипотенузы АВ. Значит, ВН = 10 : 2 = 5 см.

Ответ: 5 см расстояние от вершины В до прямой АС.

Задача 2. Построить прямоугольный треугольник по гипотенузе и острому углу.

Дано: отрезок р, угол α.

1. Построим ∠В = α.
2. Проведем окружность с центром В и радиусом р.
3. С – точка пересечения окружности и угла.
4. Построим перпендикуляр к другой стороне угла.
5. ∆АВС – искомый.

Задача 3. Построить треугольник по стороне, прилежащему к ней углу и биссектрисе треугольника, проведенной из вершины этого угла.

Дано: отрезки р и q, угол α.

Требуется построить треугольник АВС, у которого одна из сторон, например АС = р, ∠А =α , а биссектриса АD = q.

Задачи на построение. 7-й класс, геометрия

Разделы: Математика

Класс: 7

Цели урока:

максимально донести до учащихся изучаемый материал;
• развивать мышление, память, умение свободно пользоваться циркулем;
• попытаться повысить активность и самостоятельность учащихся при выполнении заданий.

Оборудование:

школьный циркуль
• транспортир,
• линейка,
• карточки для самостоятельной работы.

Тема урока: «Задачи на построение».

Сегодня мы будем учиться строить треугольники по трем заданным элементам с помощью циркуля и линейки.

Чтобы построить треугольник, нужно сначала уметь строить отрезок, равный заданному, и угол, равный заданному. Конечно, можно это сделать с помощью линейки с делениями и транспортира, но в математике требуется еще и уметь выполнять построения с помощью циркуля и линейки без делений.

Любая задача на построение включает в себя четыре основных этапа:

• анализ;
• построение;
• доказательство;
• исследование.

Анализ и исследование задачи необходимы так же, как и само построение. Необходимо посмотреть, в каких случаях задача имеет решение, а в каких – решения нет.

1. Построение отрезка, равного заданному.

2. Строим угол, равный заданному, с помощью циркуля и линейки.

А вот теперь перейдем к построению треугольников по трем элементам.

3. Построение треугольника по двум сторонам и углу между ними.

Дано	Требуется построить	Построение
1. Построить угол А, равный заданному углу. 2. На одной стороне угла отметить точку С так, чтобы отрезок АС был равен заданному отрезку b. 3. На другой стороне угла отметить точку В так, чтобы отрезок АВ был равен заданному отрезку с. 4. Соединить с помощью линейки точки В и С.

Построен треугольник АСВ по двум сторонам и углу между ними.

Самостоятельная работа к схеме 3.

Построить треугольник ВСН, если ВС = 3 см, СН = 4 см, С = 35є.

Построить треугольник СДЕ, у которого ДС = 4 см, ДЕ = 5 см, Д = 110є.

Подсказка. Перед построением треугольника необходимо сделать «от руки» чертеж треугольника, где показаны все заданные элементы.

4. Построение треугольника по стороне и прилежащим к ней углам.

Дано

Требуется построить

Построение

1. Произвольно начертить отрезок АВ, равный заданному отрезку c.
2. Построить угол А, равный заданному.
3. Построить угол В, равный заданному.

Точка пересечения двух сторон углов А и В – вершина треугольника С.

Построили треугольник АСВ по стороне и двум заданным углам.

Самостоятельная работа к схеме 4.

Построить треугольник КМО, если КО = 6 см, К = 130є, О = 20є.

Построить треугольник ВСР, если С = 15є, Д = 50є, СД = 3 см.

5. Построение треугольника по трем сторонам.

Дано

Требуется построить

Построение

1. Построить отрезок АВ, равный заданному отрезку c.
2. Из точки А провести часть окружности, радиус которой
равен заданному отрезку b.
3. Из точки В провести часть окружности, радиус которой
равен заданному отрезку a, обе окружности пересекаются в точке С.

Построили треугольник АСВ по трем сторонам.

Самостоятельная работа к схеме 5.

Построить треугольник ОДЕ, если ОД = 4 см, ДЕ = 2 см, ЕО = 3 см.

Построить треугольник МНО, если МН = 1 см, НО = 4 см, ОМ = 3 см.

После построения любого треугольника, самостоятельно провести доказательство того, что получившийся треугольник – искомый, и по возможности провести исследование.

🎥 Видео