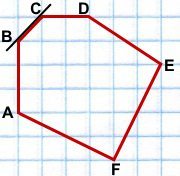
- Определение
- Выпуклый многоугольник
- Всегда ли треугольник выпуклые
- Треугольник — определение и основные свойства и виды треугольника
- Определение треугольника
- Высота треугольника
- Виды треугольника
- Виды треугольников по углам
- Виды треугольников по сторонам
- Свойства сторон треугольника
- Правило существования треугольника
- Свойство углов в треугольнике
- Элементы композиции
- Выпуклый многоугольник: определение, элементы, свойства, примеры
- Содержание:
- Элементы многоугольника
- Выпуклые и невыпуклые многоугольники
- Свойства выпуклого многоугольника
- Диагонали и углы в выпуклых многоугольниках
- Примеры
- Пример 1
- Пример 2
- Выпуклый многоугольник
- Определение
Видео:8 класс, 2 урок, Выпуклый многоугольникСкачать

Определение
Выпуклый многоугольник — это многоугольник, лежащий по одну сторону от каждой
прямой проходящей через два его соседних угла.
Правильный многоугольник — это выпуклый многоугольник,
в котором все углы и стороны равны.
Если в многоугольнике, через каждые два его соседних угла по одну сторону
проходит прямая, то многоугольник выпуклый. Многоугольник, который не
является выпуклым называется не выпуклым многоугольником.
В выпуклых многоугольниках сумма углов вычисляется по формуле: (n-2) * 180,
где n — количество сторон.
Видео:Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать

Выпуклый многоугольник
Что такое выпуклый многоугольник? В чём отличие выпуклого многоугольника от многоугольника, который не является выпуклым?
Выпуклый многоугольник — это многоугольник, лежащий в одной полуплоскости от каждой прямой, содержащей его сторону.
То есть ни одна из прямых, проходящих через две соседние вершины выпуклого многоугольника, не разрезает этот многоугольник на две части.
1) ABCDEF — выпуклый шестиугольник, так как он лежит в одной полуплоскости относительно каждой из прямых AB, BC, CD, DE и EF.
2) MNKFEL — не выпуклый шестиугольник,
Он не лежит в одной полуплоскости относительно прямых KF и FE.
Не выпуклый многоугольник можно разбить на конечное число выпуклых многоугольников. Поэтому в курсе геометрии средней школы изучают только выпуклые многоугольники.
Важнейшие виды выпуклых многоугольников
- Треугольники (в частности, прямоугольные, равнобедренные, равносторонние (правильные))
- Параллелограммы (в частности, прямоугольники, ромбы, квадраты)
- Трапеции (в частности, прямоугольные и равнобедренные)
- Правильные многоугольники.
Видео:Выпуклые и невыпуклые многоугольникиСкачать
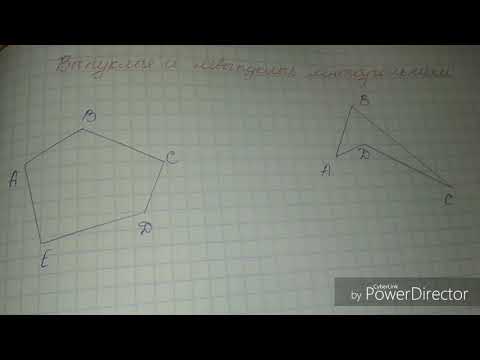
Всегда ли треугольник выпуклые
Видео:Чему равна сумма углов выпуклого многоугольникаСкачать

Треугольник — определение и основные свойства и виды треугольника
Что такое треугольник знают дети уже в самом младшем возрасте, они умеют находить треугольник среди множества геометрических фигур. Но вот уже в школе по геометрии проходят треугольник и надо не просто узнавать треугольник, но и дать определение этому понятию.
Видео:Что такое выпуклый четырёхугольник? | Математика 8 класс | Геометрия 8 класс | МегаШколаСкачать

Определение треугольника
Треугольник — это геометрическая фигура, окруженная тремя отрезками прямой (конечные точки каждых двух смежных отрезков соединены или перекрываются), называется треугольником. Точки пересечения отрезков называются вершинами треугольника, а сами отрезки между двумя соседними вершинами треугольника называются сторонами треугольника.
Посмотрите на треугольник на рисунке.
У него три вершины — 






будут звать 
По правилам математической грамотности треугольник, как и любой другой многоугольник, следует называть, начиная с левого нижнего угла и называя все вершины по часовой стрелке.
В треугольнике можно провести особенные стороны — высоту, медиану и биссектрису. Начнем с высоты треугольника.
Видео:Многоугольники. Математика 8 класс | TutorOnlineСкачать

Высота треугольника
В каждом треугольнике можно провести три высоты. Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на противолежащую этой вершине сторону.
Например, в треугольнике 

А теперь проведем из каждой вершины по высоте — получим три высоты — больше провести высот нельзя.
В этом треугольнике три высоты 


Про биссектрисы и медианы поговорим в других статьях. Сейчас же давайте с вами рассмотрим каким бывает треугольник.
Видео:№365. Сколько сторон имеет выпуклый многоугольник, каждый угол которого равенСкачать

Виды треугольника
Виды треугольника могут быть по углам и по сторонам. То есть в первом случае вид треугольника зависит от того, какие в этом треугольнике углы, а во втором случае — какие в этом треугольнике стороны.
Виды треугольников по углам
В зависимости от того, все ли углы в треугольнике острые или есть тупой угол или угол, равный
, треугольник бывает остроугольным, тупоугольным или прямоугольным.
Посмотрите на рисунки — перед вами три основных вида треугольника:
Виды треугольников по сторонам
Если у треугольника все стороны равны, то такой треугольник называют равносторонним или правильным. Если у треугольника равны только две стороны, то такой треугольник называют равнобедренным.
На рисунке показаны равносторонний и равнобедренный треугольники.
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Свойства сторон треугольника
Треугольник имеет важные свойства и характеристики.
Устойчивость — это важное свойство треугольника, оно вам еще пригодится в курсе физики. Но вначале мы с ним знакомимся на уроках геометрии.
Треугольник устойчив на любой своей стороне — то есть чтобы вывести его из состояния равновесия надо приложить силу.
Свойства сторон: разница между любыми двумя сторонами треугольника меньше, чем третья сторона, а также любая сторона треугольника меньше, чем сумма двух других сторон. То есть:
Например, пусть наш треугольник имеет длины двух сторон 

Решение: согласно свойству сторон треугольника, получим:
Таким образом, третья сторона треугольника может быть в диапазоне от 4 до 10 см. Или в целых числах ее длина может быть 5, 6, 7, 8 или 9 см.
Правило существования треугольника
Используя свойство сторон треугольника мы можем определить существует ли треугольник с определенными сторонами.
Для проверки сложите длины самых коротких сторон и если сумма их больше длины самой большой стороны, тогда треугольник существует.
Например, существует ли треугольник с длинами сторон 3, 7 и 15 см?
Решение: проверим по свойству сторон треугольника: складываем две самые короткие стороны 3 и 7 см: 3+7=10, а 10 7 — треугольник с такими длинами сторон существует.
Видео:Выпуклый многоугольник | Геометрия 7-9 класс #40 | ИнфоурокСкачать

Свойство углов в треугольнике
Сумма всех углов в треугольнике равна 
Согласно этому свойству мы всегда можем, зная два угла в треугольнике, найти его третий угол. В прямоугольном треугольнике сумма двух острых углов всегда равна 
Например, пусть известно, что в треугольнике 



Так как сумма углов в треугольнике равна 

Ответ: 
Видео:Виды угловСкачать

Элементы композиции
Многие школьники спрашивают — а зачем нам знать про треугольник, как это может пригодиться в обычной жизни? Треугольник — простая фигура из которой можно составить более сложные. Это используется во многих сферах жизни, например, вы можете эргономично убирать в своей комнате, или красиво выкладывать бутерброды. Например, из двух равных треугольников можно составить параллелограмм.
А из двух равных прямоугольных треугольником — прямоугольник или квадрат. Два треугольника могут образовать трапецию, так как на рисунке. А вот какую фигурку можно смоделировать для программируемой игры — она вся сделана из треугольников:
Мы, рассмотрели самые важные свойства треугольника, и в дальнейшем изучим еще больше разных интересных свойств, закономерностей. Несмотря на свою простоту, треугольник таит в себе много загадок и открытий.
Видео:Найдите угол: задача по геометрииСкачать

Выпуклый многоугольник: определение, элементы, свойства, примеры
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Содержание:
А выпуклый многоугольник Это геометрическая фигура, содержащаяся в плоскости, которая характеризуется тем, что все ее диагонали находятся внутри, а ее углы составляют менее 180 °. Среди его свойств можно выделить следующие:
1) Он состоит из n последовательных сегментов, в которых последний из сегментов соединяется с первым. 2) Ни один из сегментов не пересекается таким образом, чтобы ограничить плоскость во внутренней и внешней областях. 3) Каждый угол во внутренней области строго меньше плоского угла.
Простой способ определить, является ли многоугольник выпуклым или нет, — это рассмотреть линию, проходящую через одну из его сторон, которая определяет две полуплоскости. Если на каждой линии, проходящей через одну сторону, другие стороны многоугольника находятся в одной полуплоскости, то это выпуклый многоугольник.
Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Элементы многоугольника
Каждый многоугольник состоит из следующих элементов:
Стороны — это каждый из последовательных сегментов, составляющих многоугольник. В многоугольнике ни один из составляющих его сегментов не может иметь открытого конца, в этом случае будет многоугольная линия, но не многоугольник.
Вершины — это точки соединения двух последовательных отрезков. В многоугольнике количество вершин всегда равно количеству сторон.
Если две стороны или сегменты многоугольника пересекаются, значит, у вас есть перекрещенный многоугольник. Точка пересечения не считается вершиной. Поперечный многоугольник — это невыпуклый многоугольник. Звездообразные многоугольники являются перекрестными многоугольниками и поэтому не являются выпуклыми.
Когда у многоугольника все стороны одинаковой длины, мы получаем правильный многоугольник. Все правильные многоугольники выпуклые.
Видео:Как узнать сумму углов любой выпуклой фигуры? Просто!Скачать

Выпуклые и невыпуклые многоугольники
На рисунке 1 показано несколько многоугольников, некоторые из них выпуклые, а некоторые — нет. Разберем их:
Номер 1 — это трехсторонний многоугольник (треугольник), а все внутренние углы меньше 180 °, поэтому это выпуклый многоугольник. Все треугольники — выпуклые многоугольники.
Число 2 — это четырехсторонний многоугольник (четырехугольник), в котором ни одна из сторон не пересекается, а каждый внутренний угол меньше 180 °. Тогда это будет выпуклый многоугольник с четырьмя сторонами (выпуклый четырехугольник).
С другой стороны, число 3 представляет собой многоугольник с четырьмя сторонами, но один из его внутренних углов больше 180 °, поэтому он не удовлетворяет условию выпуклости. То есть это невыпуклый четырехсторонний многоугольник, называемый вогнутым четырехугольником.
Число 4 представляет собой многоугольник с четырьмя отрезками (сторонами), два из которых пересекаются. Четыре внутренних угла меньше 180 °, но поскольку две стороны пересекаются, получается невыпуклый перекрещенный многоугольник (перекрещенный четырехугольник).
Другой случай — число 5. Это многоугольник с пятью сторонами, но поскольку один из его внутренних углов больше 180 °, мы получаем вогнутый многоугольник.
Наконец, число 6, у которого также есть пять сторон, имеет все внутренние углы меньше 180º, поэтому это выпуклый многоугольник с пятью сторонами (выпуклый пятиугольник).
Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Свойства выпуклого многоугольника
1. Непересекающийся многоугольник или простой многоугольник делит содержащую его плоскость на две области. Внутренняя область и внешняя область, многоугольник является границей между двумя областями.
Но если многоугольник дополнительно выпуклый, тогда у нас есть внутренняя область, которая является односвязной, что означает, что, взяв любые две точки из внутренней области, он всегда может быть соединен сегментом, который полностью принадлежит внутренней области.
2- Каждый внутренний угол выпуклого многоугольника меньше плоского угла (180º).
3- Все внутренние точки выпуклого многоугольника всегда принадлежат одной из полуплоскостей, определяемых линией, проходящей через две последовательные вершины.
4- В выпуклом многоугольнике все диагонали полностью содержатся во внутренней многоугольной области.
5- Внутренние точки выпуклого многоугольника полностью принадлежат выпуклому угловому сектору, определяемому каждым внутренним углом.
6. Каждый многоугольник, все вершины которого находятся на окружности, является выпуклым многоугольником, который называется циклическим многоугольником.
7- Каждый циклический многоугольник является выпуклым, но не каждый выпуклый многоугольник является циклическим.
8- Каждый непересекающийся многоугольник (простой многоугольник), все стороны которого равны, является выпуклым и известен как правильный многоугольник.
Видео:Теперь ты будешь находить углы за секунды. Как найти внешний угол треугольника? #математика #углыСкачать

Диагонали и углы в выпуклых многоугольниках
9- Общее количество N диагоналей выпуклого многоугольника с n сторонами определяется по следующей формуле:
Доказательство. В выпуклом многоугольнике с n сторонами каждой вершины нарисовано n — 3 диагоналей, так как сама вершина и две соседние вершины исключены. Поскольку имеется n вершин, всего нарисовано n (n — 2) диагоналей, но каждая диагональ была нарисована дважды, поэтому количество диагоналей (без повторения) равно n (n-2) / 2.
10- Сумма S внутренних углов выпуклого многоугольника с n сторонами определяется следующим соотношением:
Доказательство. Из вершины выводятся n-3 диагонали, определяющие n-2 треугольника. Сумма внутренних углов каждого треугольника составляет 180º. Общая сумма углов n-2 треугольников равна (n-2) * 180º, что совпадает с суммой внутренних углов многоугольника.
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Примеры
Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Пример 1
Циклический шестиугольник — это многоугольник с шестью сторонами и шестью вершинами, но все вершины находятся на одной окружности. Каждый циклический многоугольник выпуклый.
Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Пример 2
Определите значение внутренних углов обычного энегона.
Решение: enegon — это 9-сторонний многоугольник, но если он также правильный, все его стороны и углы равны.
Сумма всех внутренних углов 9-стороннего многоугольника равна:
S = (9 — 2) 180º = 7 * 180º = 1260º
Но существует 9 внутренних углов одинаковой меры α, поэтому должно выполняться равенство:
Отсюда следует, что мера α каждого внутреннего угла правильного ребра равна:
α = 1260º/9 = 140º
Как расслабиться в офисе? 12 практических советов
Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Выпуклый многоугольник
Определение
Выпуклый многоугольник — это многоугольник, лежащий по одну сторону от каждой
прямой проходящей через два его соседних угла.
Правильный многоугольник — это выпуклый многоугольник,
в котором все углы и стороны равны.
Если в многоугольнике, через каждые два его соседних угла по одну сторону
проходит прямая, то многоугольник выпуклый. Многоугольник, который не
является выпуклым называется не выпуклым многоугольником.
В выпуклых многоугольниках сумма углов вычисляется по формуле: (n-2) * 180,
где n — количество сторон.