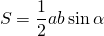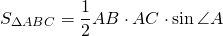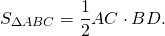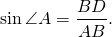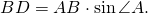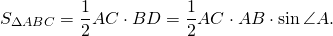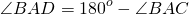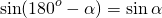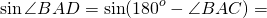Видео:✓ Новая формула площади треугольника | Ботай со мной #108 | Борис ТрушинСкачать
Площадь треугольника через синус
Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать
Определение
Площадь треугольника через синус — это площадь треугольника,
выраженная через две любые стороны треугольника и синус угла между ними.
Синус угла — это число, которое используется для нахождения
разных величин в треугольниках, его можно найти в специальных таблицах.
Видео:9 класс, 12 урок, Теорема о площади треугольникаСкачать
Введение
Площадь треугольника кроме половины произведения высоты
на основания, можно также найти и другим способом.
Мало кто знает, но через синусы углов можно найти обычно
не только стороны, но и площадь любого треугольника!
Площадь треугольника выраженная без синуса численно равна
половине произведения двух сторон друг на друга
на синус угла между ними.
Площадь треугольника через синус ищется только в том случае,
если по другой формуле площадь треугольника найти нельзя.
Теорема
( S = frac2 * BC * AC * sin angle BCA )
Площадь произвольного треугольника равна полусумме
произведения двух любых сторон треугольника друг на друга,
и на синус угла между этими сторонами.
Формула
[ S = frac2 * a * b * sin α ]
Где a, b — две стороны треугольника, синус α — синус угла α.
Пример
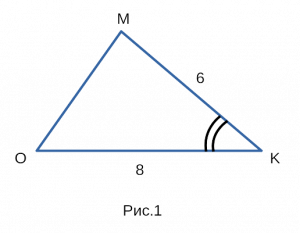
Для примера, возьмем треугольник omk, изображенный на рисунке 1, со сторонами om, mk, ok.
Известно, что mk равен 6, ok равен 8, синус угла okm равен 1/4.
Нужно найти площадь треугольника omk.
Дано: △omk, mk = 6, ok = 8, sin okm = 1/4.
Найти: S △omk — ?
Решение:
1) ( S = frac2*a*b*sin α ) ( implies ) ( S = frac2*mk*ok*sin okm )
2) S = 1/2 * 6 * 8 * 1/4 = 1/2 * 6 * 8 * 0.25 = 1/2 * 48 * 0.25 = 1/2 * 12 = 6
Ответ: Площадь треугольника omk равна 6.
Доказательство
Докажем, что площадь произвольного треугольника
равна полусумме произведения двух любых сторон
друг на друга, и на синус угла между этими сторонами.
Чтобы вам наглядно было видно, как мы доказываем,
используем один из известнейших треугольников — египетский треугольник.
Высота в египетском треугольнике равна длине одного из катетов.
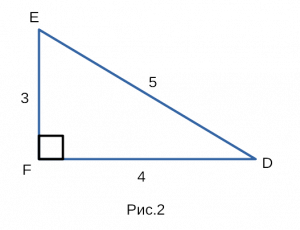
Построим прямоугольный треугольник, изображенный на рисунке 2,
со сторонами 3,4,5 с одним из углов 90 градусов.
Первым делом найдем площадь обычной формулой,
затем с помощью синуса. Площадь равна половине
основания на высоту — ½3*4 = 6. Теперь найдем с
помощью синуса: ½3*4*sin90 = 6 * 1 = 6. Как видим,
полученные значения площадей сходятся, соответственно
через синус можно найти площадь треугольника ч.т.д.
Теперь, чтобы найти площадь треугольника нам не нужно
знать основание и высоту, можно знать только
две стороны и синус угла между ними.
Видео:Геометрия 9 класс (Урок№14 - Теорема о площади треугольника.)Скачать
Заключение
В заключение, можно сказать, что площадь
треугольника можно найти разными способами.
Например, в прямоугольном треугольнике площадь
рассчитать легче чем в любом другом треугольнике,
так как высота уже известна. Именно поэтому,
в школьном курсе, отчасти так подробно изучаются
прямоугольные треугольники. В Древнем Египте были
распространены прямоугольные треугольники со
сторонами 3,4,5; 6,8,10; 5,12,13. Длины этих прямоугольных
треугольников треугольников целые, что значительно,
упрощало разного рода вычисления.
Формулу площади треугольника делает универсальной то,
что она может применена к абсолютно любым треугольникам.
Главное, чтобы были известные две стороны,
и угол или синус угла между ними.
Формула площади треугольника через синус — универсальна,
поэтому может быть применена к любым видам треугольников.
Видео:Площадь треугольника через синус угла.Решение прямоугольных треугольников.8класс.Скачать
Площадь треугольника по двум сторонам
Выясним, как найти площадь треугольника по двум сторонам.
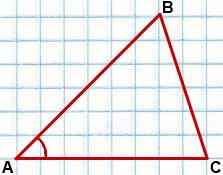
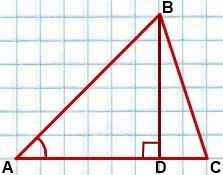
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Формула площади треугольника по двум сторонам:
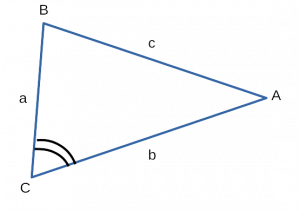
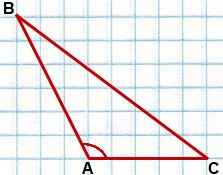
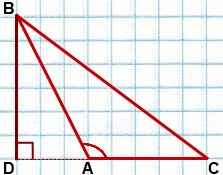
Проведем в треугольнике ABC высоту BD.
равна половине произведения его стороны на высоту, проведенную к этой стороне:
Рассмотрим треугольник ABD — прямоугольный (так как BD — высота по построению).
По определению синуса острого угла в прямоугольном треугольнике,
Если в треугольнике ABC
то в треугольнике ABD
То есть, и в случае тупого угла A выполняется равенство
Видео:100. Теорема о площади треугольникаСкачать
Формулировка теоремы о площади треугольника:
Видео:Геометрия Доказательство Площадь треугольника равна половине произведения двух его сторон и синусаСкачать
Доказательство:
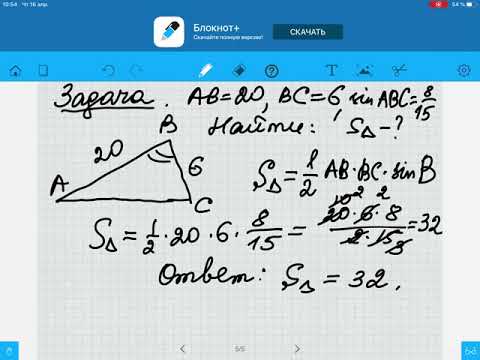
Рассмотрим произвольный треугольник ABC. Пусть в нем сторона BC = a, сторона CA = b и S – площадь этого треугольника. Необходимо доказать, что S = (1/2)*a*b*sin(C).
Для начала введем прямоугольную систему координат и поместим начало координат в точку С. Расположим нашу систему координат так, чтобы точка B лежала на положительном направлении оси Сх, а точка А имела бы положительную ординату.
Если все выполнить правильно, то должен получится следующий рисунок.
Площадь данного треугольника можно вычислить по следующей формуле: S = (1/2)*a*h, где h — это высота треугольника. В нашем случае высота треугольника h равна ординате точки А, то есть h = b*sin(C).
Учитывая полученные результат, формулу площади треугольника можно переписать следующим образом: S = (1/2)*a*b*sin(C). Что и требовалось доказать.
📺 Видео
Как найти площадь треугольника? #треугольник #математика #егэ #shorts #подготовкакегэ #огэ #площадьСкачать
9 класс, 13 урок, Теорема синусовСкачать
9 класс "Площадь треугольника через синус"Скачать
ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать
Запомни: все формулы для площади треугольникаСкачать
8 класс, 14 урок, Площадь треугольникаСкачать
Площадь треугольника через синус | до автоматизма | математикаСкачать
Геометрия. Теорема синусов и косинусов. Площадь треугольника.Скачать
Учимся вычислять площадь треугольника через синус угла между его сторонамиСкачать
Решение задачи с применением теоремы синусовСкачать
Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать
Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать
Геометрия 9 класс : Теорема о площади треугольникаСкачать
