Треугольник — это замкнутая ломаная линия, состоящая из трёх звеньев:
Вершины ломаной называются вершинами треугольника, а её звенья — сторонами треугольника. Углы, образованные двумя сторона треугольника, называются углами треугольника:
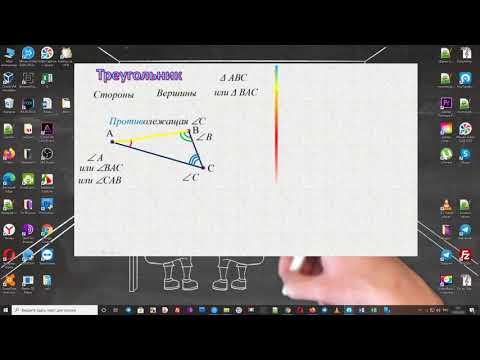
В треугольнике ABC вершины A, B и C — это вершины треугольника, звенья AB, BC и CA — стороны треугольника. Три угла — ∠ABC, ∠BCA и ∠CAB — углы треугольника. Часто углы треугольника обозначаются только одной буквой: ∠A, ∠B, ∠C.
Треугольник обычно обозначается тремя буквами, стоящими при его вершинах. Например, треугольник ABC, или BCA, или CBA. Вместо слова треугольник часто используется знак 

У каждого треугольника 3 вершины, 3 стороны и 3 угла.
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Высота
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на его основание. Высота треугольника может быть опущена и на продолжение основания.
Отрезок BN — это высота 

Длина высоты — это длина отрезка от вершины угла до пересечения с основанием.
Каждый треугольник имеет три высоты.
Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Биссектриса
Биссектриса угла треугольника — прямая, делящая угол треугольника пополам. Длина отрезка этой прямой от вершины угла до точки пересечения с противоположной стороной называется длиной биссектрисы.
Отрезок BN — это биссектриса 
Каждый треугольник имеет три биссектрисы.
Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Медиана
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Длина этого отрезка называется длиной медианы.
Отрезок BN — это медиана 
Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Вершина треугольника – определение
В геометрии нередко рассматривают такое понятие, как «вершина треугольника». Это точка пересечения двух сторон данной фигуры. Практически в каждой задаче встречается это понятие, поэтому имеет смысл рассмотреть его более подробно.
Видео:Вершины треугольникаСкачать
Определение вершины треугольника
В треугольнике есть три точки пересечения сторон, образующие три угла. Их называют вершинами, а стороны, на которые они опираются – сторонами треугольника.
Рис. 1. Вершина в треугольнике.
Вершины в треугольниках обозначают большими латинскими буквами. Поэтому чаще всего в математике стороны обозначают двумя заглавными латинскими буквами, по названию вершин, которые входят в стороны. Например стороной АВ называют сторону треугольника, соединяющую вершины А и В.
Рис. 2. Обозначение вершин в треугольнике.
Видео:Вычисляем высоту через координаты вершин 1Скачать

Характеристики понятия
Если взять произвольно ориентированный в плоскости треугольник, то на практике очень удобно выразить его геометрические характеристики через координаты вершин этой фигуры. Так, вершину А треугольника можно выразить точкой с определенными числовыми параметрами А(х; y).
Зная координаты вершин треугольника можно найти точки пересечения медиан, длину высоты, опущенную на одну из сторон фигуры, и площадь треугольника.
Для этого используются свойства векторов, изображаемых в системе декартовой системе координат, ведь длина стороны треугольника определятся через длину вектора с точками, в которых находятся соответствующие вершины этой фигуры.
Видео:Построение высоты в треугольникеСкачать

Использование вершины треугольника
При любой вершине треугольника можно найти угол, который будет смежным внутреннему углу рассматриваемой фигуры. Для этого придется продлить одну из сторон треугольника. Поскольку сторон при каждой вершин две, то и внешних углов при каждой вершине два. Внешний угол равен сумме двух внутренних углов треугольника, несмежных с ним.
Рис. 3. Свойство внешнего угла треугольника.
Если построить при одной вершине два внешних угла, то они будут равны, как вертикальные.
Видео:№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

Что мы узнали?
Одним из важных понятий геометрии при рассмотрении различных типов треугольников является вершина. Это точка, где пересекаются две стороны угла данной геометрической фигуры. Ее обозначают одной из больших букв латинского алфавита. Вершину треугольника можно выразить через координаты x и y, это помогает определять длину стороны треугольника как длину вектора.
Видео:Первый признак равенства треугольников. 7 класс.Скачать

Геометрия
План урока:
Видео:Построение медианы в треугольникеСкачать

Как выглядит треугольник?
В выходной день Глеб с родителями ехали в парк. Мальчик заметил, что вдоль дороги стояла непонятная табличка, увидев которую, отец поехал очень медленно.
«Что это такое?» – поинтересовался ребенок. Папа рассказал, что это дорожный знак, который предупреждает о трудностях на пути. Глебу очень понравился знак, а особенно его форма. Отец продолжил рассказ о знаках: «Форма знака о многом говорит водителю, ведь при плохой видимости автолюбитель видит только форму, а не надпись. Поэтому все предупреждающие знаки – треугольные». «А что такое треугольные?» – не унимался мальчик. Найти ответ на этот и многие другие вопросы папе помог наш сегодняшний урок.
Вначале, давайте разберемся, что же такое треугольник и из чего он состоит.
В повседневной жизни нас окружает масса предметов имеющих треугольную форму. Например:
Часы, воздушный змей, кусочек торта, пиццы, арбуза, салатники, рамки для фотографий, пузырек парфюма – этот список можно продолжать бесконечно. Но что же такое треугольник?
Приведем примеры треугольников:
Исходя из определения, каждый рисунок состоит из трех отрезков. В геометрии такие отрезки называют сторонами треугольника.
Кроме отрезков, составляющей частью фигуры являются три точки, которые принято называть вершинами.
В геометрии, вершины треугольника принято обозначать заглавными буквами латиницы: A,C,D,B.
Начертим треугольник. Вершины, обозначим буквами A,C,D.
Данная геометрическая фигура имеет три вершины A,C,D и три стороны АС, CD, DА.
А как же на письме показать, что данная фигура является треугольником?
Очень интересным является то, что записывать название, можно перечисляя вершины в любом порядке.
Можно записать: ∆NOK, ∆OKN, ∆KNО. Каждый вариант записи обозначает один и тот же треугольник и является верным.
Само название фигуры «Треугольник» предполагает, что в состав должны входить три угла. Так ли это?
Внимательно рассмотрим рисунок:
Действительно, мы видим три угла, которые отмечены дугами: ∠RFP,∠FPR, ∠PRF(мы уже знаем, что буква, обозначающая вершину угла всегда записывается в середине) или∠F, ∠P,∠R.
Видео:Уравнения стороны треугольника и медианыСкачать

Виды треугольников
Все геометрические фигуры, имеющие треугольную форму,делятся на группы по двум направлениям:
Давайте рассмотрим, на какие группы делятся треугольники по углам:
Теперь, познакомимся с группами треугольников по сторонам(на рисунках равные стороны принято обозначать одинаковым количеством черточек):
Постарайтесь запомнить все виды треугольников, так как на протяжении всего учебного процесса, вам часто придется сталкиваться с выполнением заданий на данную тему.
Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Равенство треугольников
Случаются ситуации, когда точно известно, что два треугольника равны, а что же в таком случае можно сказать про углы и стороны таких треугольников?
Нам дано: ∆ABC = ∆A1B1C1. Равны ли соответствующие стороны и углы данных фигур?
По условию треугольники равны. Значит, применяем рассмотренное правило, которое говорит о том, что все соответствующие элементы фигуры равны между собой.
Если ∆ABC = ∆A1B1C1, то равны соответствующие стороны:
и соответствующие углы равны:
Геометрия интересна тем, что большинство её правил нуждаются в доказательствах. Такие правила называют теоремами.
Вместе с этим, имеются и самостоятельные правила, которые называют аксиомами геометрии.
Сегодня мы рассмотрим первую теорему с названием «Первый признак равенства треугольников», и проведем работу по сбору доказательств для данной теоремы.
Два треугольника – ∆OMN и ∆KLT. Известно, что две стороны треугольников и угол между ними равны.
Докажем, что ∆OMN=∆KLT.
Доказательство первого признака равенства треугольников:
Из условия нам известно, что соответствующие углы равны ∠M =∠L, следовательно, мы можем выполнить наложение двух треугольников так, чтобы вершина M совпадала с вершиной L.
Тогда, сторона OM наложится на сторону KL, а сторона MN на отрезок LT. По условию нам известно, что отрезки равны OM=KL, MN=LT, значит, при наложении они совпадут. Получается, что при наложении совпадает угол, и две стороны, следовательно, будут совпадать и оставшиеся стороны ON и KT, то есть ON = KT . Если при наложении совмещаются три стороны и одна вершина, значит, совместятся и две другие вершины KO и TN.
Выходит, что при совмещении совпадают все элементы ∆, а такие ∆ называются равными.
Мы доказали, что ∆OMN=∆KLT.
Еще, нам предстоит познакомиться с несколькими понятиями, без которых продолжать изучение геометрии невозможно.
Начертим прямую АВ. Выберем точку не лежащую на данной прямой. Проведем отрезок СК, соединяющий точку С и прямую АВ, таким образом, чтобы при пересечении СК и АВ образовывался прямой угол (90˚) . Изображенный отрезок СК называют перпендикуляром к прямой.
Доказательство будем проводить в два этапа.
Видео:Высоты треугольника.Скачать

Медиана, биссектриса, высота
Рассмотрим ∆АВС. Отметим на отрезке АС середину и обозначим её точкой О. Соединим точки В и О отрезком. Полученный отрезок ВО называют медианой.
Любой треугольная фигура имеет три вершины, из каждой можно провести медиану, следовательно, в одной можно провести три медианы.
Биссектриса
Чтобы рассмотреть понятие биссектрисы треугольника, вспомним определение биссектрисы угла:
На рисунке изображен ∆ОВМ. Из угла О проведем биссектрису (луч, делящий угол пополам)и продолжим её до пересечения со стороной ВМ. Место пересечения отметим точкой С. Отрезок ОС делит угол О пополам(∠ВОС =∠СОМ) и пересекается с противолежащей стороной ВМ.
На рисунке изображена фигура РТК. Из вершины Т проведем перпендикуляр к стороне РК, место пересечения перпендикуляра и стороны фигуры отметим точкой А.∠ТАК =∠ТАР=90˚. Перпендикуляр ТА называют высотой ∆РТК.
Изученные сегодня определения и теоремы являются базовыми в изучении геометрии. Поэтому постарайтесь уделить особое внимание материалу сегодняшнего урока.
🔥 Видео
Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Треугольники. 7 класс.Скачать

Равнобедренный треугольник. 7 класс.Скачать

Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Медиана, высота и биссектриса треугольника. Центроид, инцентр, ортоцентр. Геометрия 7 класс.Скачать

Как найти расстояние от вершины треугольника до ортоцентра? Профиматика и ЕГЭматика знают ответ!Скачать

6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать









