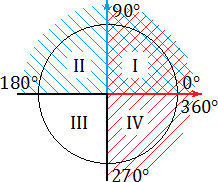
Если посмотреть на числовую окружность , то можно заметить, что оси абсцисс и ординат разбивают ее на четыре части. Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки).

(() (frac) (;2π)) — четвертая четверть
Видео:Тригонометрическая окружность. Как выучить?Скачать

Почему так важно определять какой четверти принадлежит угол?
Дело в том, что каждая четверть уникальна в плане знаков тригонометрических функций .
Например, для любого угла из второй четверти — синус положителен, а косинус , тангенс и котангенс отрицательны. А для любого угла из первой четверти — все четыре функции будут положительны.
Теперь давайте рассмотрим пример задачи, которую не решить без использования знаний про четверти.
Пример (ЕГЭ):
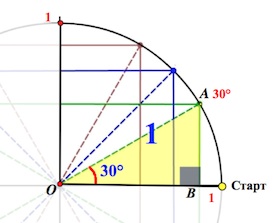
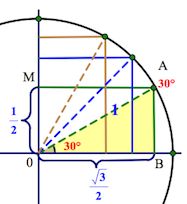
 ((0;-) (frac) ()) — четвертая четверть Ну и, конечно, мы можем в отрицательную сторону делать обороты, так же как и в положительную. Видео:10 класс, 11 урок, Числовая окружностьСкачать  Тригонометрический круг. Основные значения тригонометрических функцийЕсли вы уже знакомы с тригонометрическим кругом , и хотите лишь освежить в памяти отдельные элементы, или вы совсем нетерпеливы, – то вот он, тригонометрический круг : Мы же здесь будем все подробно разбирать шаг за шагом + показать Тригонометрический круг – не роскошь, а необходимость Очень важно не махать рукой на значения тригонометрических функций, – мол, всегда можно посмотреть в шпору с таблицей значений. Если вы постоянно смотрите в таблицу со значениями тригонометрических формул, давайте избавляться от этой привычки! Нас выручит тригонометрический круг ! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове. Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ! К примеру, скажите, глядя в стандартную таблицу значений тригонометрических формул , чему равен синус, скажем, Никак. можно, конечно, подключить формулы приведения… А глядя на тригонометрический круг, легко можно ответить на такие вопросы. И вы скоро будете знать как! А при решении тригонометрических уравнений и неравенств без тригонометрического круга – вообще никуда. Знакомство с тригонометрическим кругомДавайте по порядку. Сначала выпишем вот такой ряд чисел: И, наконец, такой: Конечно, понятно, что, на самом-то деле, на первом месте стоит Но как красиво она получилась! В случае чего – восстановим эту «лесенку-чудесенку». И зачем оно нам? Эта цепочка – и есть основные значения синуса и косинуса в первой четверти. Начертим в прямоугольной системе координат круг единичного радиуса (то есть радиус-то по длине берем любой, а его длину объявляем единичной). От луча «0-Старт» откладываем в направлении стрелки (см. рис.) углы
Это почему же, спросите вы? Не будем разбирать все. Рассмотрим принцип, который позволит справиться и с другими, аналогичными ситуациями. Треугольник АОВ – прямоугольный, в нем Значит, АВ= Надеюсь, уже что-то становится понятно? Так вот точка В и будет соответствовать значению Аналогично с остальными значениями первой четверти. Как вы понимаете, привычная нам ось (ox) будет осью косинусов , а ось (oy) – осью синусов . Про тангенс и котангенс позже. Слева от нуля по оси косинусов (ниже нуля по оси синусов) будут, конечно, отрицательные значения. Итак, вот он, ВСЕМОГУЩИЙ тригонометрический круг , без которого никуда в тригонометрии. А вот как пользоваться тригонометрическим кругом, мы поговорим в следующей статье. Видео:Найти знак тригонометрической функции (bezbotvy)Скачать  Знаки тригонометрических функцийЗнак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент. В прошлый раз мы учились переводить аргументы из радианной меры в градусную (см. урок «Радианная и градусная мера угла»), а затем определять эту самую координатную четверть. Теперь займемся, собственно, определением знака синуса, косинуса и тангенса.
угла α — это абсцисса (координата x ) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α. угла α — это отношение синуса к косинусу. Или, что то же самое, отношение координаты y к координате x . Обозначение: sin α = y ; cos α = x ; tg α = y : x . Все эти определения знакомы вам из курса алгебры старших классов. Однако нас интересуют не сами определения, а следствия, которые возникают на тригонометрической окружности. Взгляните: Синим цветом обозначено положительное направление оси OY (ось ординат), красным — положительное направление оси OX (ось абсцисс). На этом «радаре» знаки тригонометрических функций становятся очевидными. В частности:
В заключение рассмотрим несколько более сложных задач. Помимо выяснения знака тригонометрической функции, здесь придется немного посчитать — именно так, как это делается в настоящих задачах B11. В принципе, это почти настоящие задачи, которые действительно встречается в ЕГЭ по математике.
Поскольку sin 2 α = 0,64, имеем: sin α = ±0,8. Осталось решить: плюс или минус? По условию, угол α ∈ [π/2; π] — это II координатная четверть, где все синусы положительны. Следовательно, sin α = 0,8 — неопределенность со знаками устранена.
Действуем аналогично, т.е. извлекаем квадратный корень: cos 2 α = 0,04 ⇒ cos α = ±0,2. По условию, угол α ∈ [π; 3π/2], т.е. речь идет о III координатной четверти. Там все косинусы отрицательны, поэтому cos α = −0,2.
Имеем: sin 2 α = 0,25 ⇒ sin α = ±0,5. Снова смотрим на угол: α ∈ [3π/2; 2π] — это IV координатная четверть, в которой, как известно, синус будет отрицательным. Таким образом, заключаем: sin α = −0,5.
Все то же самое, только для тангенса. Извлекаем квадратный корень: tg 2 α = 9 ⇒ tg α = ±3. Но по условию угол α ∈ [0; π/2] — это I координатная четверть. Все тригонометрические функции, в т.ч. тангенс, там положительны, поэтому tg α = 3. Все! 🔍 ВидеоЗнаки синуса, косинуса, тангенса ЛекцияСкачать  Вычисление значений тригонометрических функцийСкачать  ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать  Как запомнить тригонометрический круг специально ничего не выучивая?Скачать  Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать  Знаки тригонометрических функций. 9 класс.Скачать  РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать  12 часов Тригонометрии с 0.Скачать  🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать  Алгебра 10 класс. 2 октября. Тангенс и котангенс на окружностиСкачать  18+ Математика без Ху!ни. Формулы ПриведенияСкачать  Таблица значений тригонометрических функций - как её запомнить!!!Скачать  Задание №13. Как отбирать корни в тригонометрической окружности? 🤔Скачать  Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать  Как найти координаты точек на тригонометрической окружностиСкачать  ЗНАЧЕНИЯ СИНУСА И КОСИНУСА НА ОКРУЖНОСТИСкачать  |


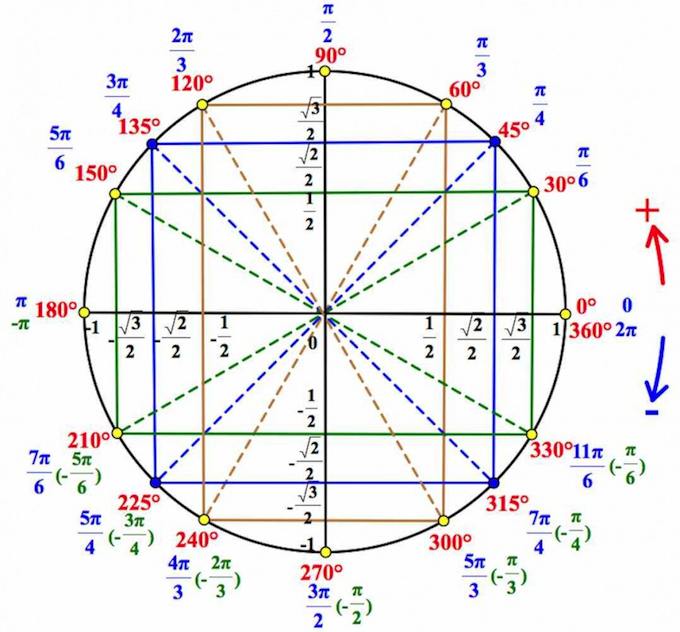
 Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…
Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…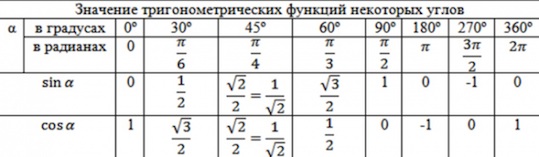
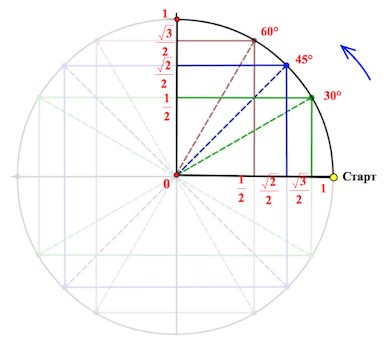 Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.
Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.