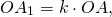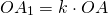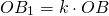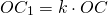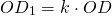Как найти центр гомотетии треугольников (5 видео)

Гомотетия

Гомотетия — это преобразование, при котором каждой точке A ставится в соответствие точка A1, лежащая на прямой OA, по правилу

где k — постоянное, отличное от нуля число, O — фиксированная точка.

Точка O называется центром гомотетии, число k — коэффициентом гомотетии.

гомотетия с коэффициентом k>0

Чтобы построить четырёхугольник, гомотетичный 4-угольнику ABCD с центром гомотетии в точке O и коэффициентом k, k>0, нужно провести лучи с началом в точке O, проходящие через вершины A, B, C, D, отложить на них отрезки соответствующей длины:

и соединить вершины A1, B1, C1и D1 отрезками.

При k

и соединить вершины A1, B1, C1 отрезками.

При гомотетии с коэффициентом k=1 каждая точка переводится сама в себя.

При k= -1 гомотетия является симметрией относительно центра O (то есть центральная симметрия является частным случаем гомотетии).

Гомотетия есть преобразование подобия. Следовательно, гомотетия обладает свойствами подобия.

Свойства преобразования гомотетии

1) При гомотетии прямые переходят в прямые, полупрямые- в полупрямые, отрезки — в отрезки, углы — в углы.

2) Сохраняются углы между полупрямыми (соответственно, сохраняется параллельность прямых).

Стороны гомотетичных фигур пропорциональны. а углы — равны.

Содержание

Как найти центр гомотетии треугольников
Применение геометрических преобразований к решению задач
ПРИМЕНЕНИЕ ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ К РЕШЕНИЮ ЗАДАЧ
🔥 Видео

Видео:ГомотетияСкачать

Как найти центр гомотетии треугольников

Документальные учебные фильмы. Серия «Геометрия».

Преобразование плоскости называется преобразованием подобия или просто подобием, если существует такое число , что для любых двух точек А и В и их образов А’ и В’ выполняется равенство . Число называется коэффициентом подобия.
При =1 преобразование подобия сохраняет расстояния, т. е. является движением. Следовательно, движение — частный случай преобразования подобия. Рассмотрим пример преобразования подобия, отличного от движения.
Зададим точку М₀ и вещественное число . Каждой точке М плоскости поставим в соответствие точку М’ так, чтобы

Такое отображение является преобразованием плоскости и называется гомотетией. Точка М₀ называется центром гомотетии, а число m — коэффициентом гомотетии. Докажем, что гомотетия — преобразование подобия. Действительно, пусть М₁, М₂ — произвольные точки плоскости, а и — их образы. Из равенства (1) получаем: , поэтому

Отсюда получаем: . Таким образом, гомотетия с коэффициентом m является преобразованием подобия с коэффициентом подобия .
При m = 1 из равенства (1) получаем: . Отсюда следует, что любая точка М плоскости совпадает с ее образом, т. е. гомотетия с коэффициентом m = 1 является тождественным преобразованием. При m = — 1 из равенства (1) получаем, что гомотетия — центральная симметрия. В остальных случаях (т. е. когда ) гомотетия — преобразование подобия, отличное от движения, т. е. преобразование плоскости, не сохраняющее расстояния между точками.

Выберем ортонормированный репер (О, Е₁, E₂) так, чтобы точка О совпала с центром гомотетии. Если М (х, у) —произвольная точка плоскости, а точка M′ (х’, у’) — ее образ, то из формулы (1) получаем аналитическое выражение гомотетии:
. (3)

Рассмотрим простейшие свойства гомотетии.

1) Гомотетия с коэффициентом переводит прямую, не проходящую через центр гомотетии, в параллельную ей прямую, а прямую, проходящую через центр гомотетии, — в себя.

□ Пусть Ах+Ву+С = 0 — уравнение данной прямой . Подставив сюда значения х, у из (3), получаем уравнение образа этой прямой: Ах’+By’+Сm = 0. Этим уравнением определяется прямая. Если С ≠ 0, то || , а если С = 0, то и совпадают.

2) Гомотетия сохраняет простое отношение трех точек.

□ Пусть А, В и С — три точки прямой, а А′, В’ и С’ — их образы, и . По определению простого отношения трех точек имеем: . По формуле (2) получаем: , где m — коэффициент гомотетии. Следовательно, . Таким образом, , т. е. (АВ, С) = (А’В’, С’).

Из этих свойств следует, что гомотетия переводит отрезок в отрезок, луч в луч и полуплоскость в полуплоскость.

3) Гомотетия переводит угол в равный ему угол.

□ Пусть ВАС — данный угол, а В′ А′ С’ — образы точек В, А и С. По формуле (2) получаем:

Отсюда следует, что

4) Гомотетия сохраняет ориентацию плоскости.

□ Пусть (А, В, С) — произвольный репер, а (А′, В’, С’) — его образ. Используя формулы (4), получаем: . Итак, в гомотетии любой репер и его образ ориентированы одинаково, т. е. гомотетия сохраняет ориентацию плоскости.

Нетрудно доказать, что если и — преобразования подобия с коэффициентами и , то — преобразование подобия с коэффициентом . Действительно, является преобразованием плоскости. Докажем, что для любых двух точек А и В и их образов A’ = ( ) (А), B’ = ( ) (В) выполняется равенство A’B’= AB. Если А₁= (А), B₁=( B), то А’ = (А₁), B’ = (B₁). По определению подобия А₁В₁ = АВ, А’В’ = A₁B₁, поэтому А’В’ = AB.

Теорема 1. Пусть — преобразование подобия с коэффициентом , a h — гомотетия с тем же коэффициентом и с центром в произвольной точке М₀. Тогда существует одно и только одно движение такое, что

Оно является преобразованием подобия с коэффициентом , т.е. движением. Из равенства (6) получаем: , или . Таким образом, существует движение , удовлетворяющая условия (5).

Пусть теперь — произвольное движение, удовлетворяющее равенству . Отсюда получаем: . Учитывая равенство (6), мы приходим к выводу, что = .

Гомотетия обладает всеми свойствами 1° — 8° движений. Доказанная теорема позволяет заключить, что и преобразование подобия обладает теми же свойствами. Следовательно, имеет место утверждение: преобразование подобия прямую переводит в прямую, параллельные прямые — в параллельные прямые, сохраняет простое отношение трех точек, полуплоскость переводит в полуплоскость, отрезок — в отрезок, луч — в луч. Преобразование подобия угол переводит в равный ему угол, а перпендикулярные прямые — в перпендикулярные прямые.
Итак, доказано, что любое преобразование подобия можно представить в виде (5): , где — движение, a — гомотетия. Так как сохраняет ориентацию плоскости, т. е. любой репер переводит в репер той же ориентации, то если сохраняет ориентацию плоскости, то, очевидно, и сохраняет ориентацию плоскости, а если меняет ориентацию плоскости, то и меняет ориентацию плоскости. Таким образом, любое преобразование подобия либо сохраняет ориентацию плоскости, либо меняет ее ориентацию. В первом случае оно называется преобразованием подобия первого рода, а во втором случае — преобразованием подобия второго рода.

Пусть — преобразование подобия коэффициентом . Выберем прямоугольную систему координат и найдем аналитическое выражение преобразования в системе . Для этого рассмотрим гомотетию с центром О и коэффициентом и воспользуемся теоремой 1. Пусть — движение, удовлетворяющее равенству (5). Запишем в системе аналитические выражения преобразований и :

Таким образом, если М (х, у) — произвольная точка плоскости, а М'(х′, у’) — ее образ в преобразовании то

где =1, если — преобразование подобия первого рода, и = — 1, если — преобразование подобия второго рода. Используя формулы (7), докажем теорему.

Теорема 2. Любое преобразование подобия, отличное от движения, имеет одну и только одну неподвижную точку.

□ Пусть равенства (7) — аналитическое выражение данного преобразования подобия. Точка М (х, у) является неподвижной точкой этого преобразования тогда и только тогда, когда

Рассмотрим определитель этой системы. Если =1, то , а если = — 1, то . Таким образом, при для любого имеем: . Отсюда следует утверждение теоремы.
Следствие. Любое преобразование подобия, имеющее более чем одну неподвижную точку или не имеющее неподвижных точек, является движением.
Используя доказанную теорему и ее следствие, можно провести классификацию преобразований подобия в зависимости от наличия неподвижных точек и инвариантных прямых.
А. Классификация преобразований подобия первого рода. Пусть f — преобразование подобия первого рода. Если f имеет более чем одну неподвижную точку или не имеет неподвижных точек, то по следствию предыдущей теоремы оно является движением, поэтому — параллельный перенос.
Остается рассмотреть случай, когда преобразование с коэффициентом имеет только одну неподвижную точку, которую обозначим через О. Пусть — гомотетия с коэффициентом и центром О. По теореме 1 существует такое движение , что . Так как и — подобия первого рода, то — движение первого рода, причем . Таким образом, — поворот вокруг точки О. Возможны три случая.

1) — тождественное преобразование. В этом случае , т. е. — гомотетия с положительным коэффициентом , .

2) — центральная симметрия. Ясно, что в этом случае — гомотетия с отрицательным коэффициентом .

3) — вращение на угол ; . В этом случае является произведением гомотетии на вращение . Оно называется центрально-подобным вращением.

Таким образом, преобразование подобия, имеющее только одну неподвижную точку, является либо гомотетией с коэффициентом , либо центрально-подобным вращением.

В. Классификация преобразований подобия второго рода. Пусть — преобразование подобия второго рода. Если имеет более чем одну неподвижную точку или не имеет неподвижных точек, то по аналогии со случаем А мы приходим к выводу, что преобразование является либо осевой симметрией, либо скользящей симметрией.
Рассмотрим случай, когда преобразование подобия с коэффициентом имеет только одну неподвижную точку О. Ясно, что , так как в противном случае — движение второго рода, но оно не может иметь только одну неподвижную точку. Пусть — гомотетия с коэффициентом к и центром О. По теореме 1 , где — движение второго рода. Точка О — неподвижная точка движения , поэтому — осевая симметрия. В этом случае называется центрально-подобной симметрией.

Итак, существует шесть типов преобразования подобия, которые приведены в следующей таблице:

Преобразование пространства называется преобразованием подобия или просто подобием, если существует такое число , что для любых двух точек А и В и их образов А’ и В’ выполняется равенство . Число называется коэффициентом подобия.
При преобразование подобия сохраняет расстояния, т. е. является движением. Следовательно, движение — частный случай подобия. Примером преобразования подобия, отличного от движения, является гомотетия, которая в пространстве вводится точно так же, как и в плоскости. Зададим точку М₀ и вещественное число . Каждой точке М поставим в соответствие точку М’ так, чтобы

Это отображение называется гомотетией с центром Мо и коэффициентом m. Для двух точек M₁ и М₂ и их образов и из формулы (1) получаем:

Отсюда следует, что . Таким образом, гомотетия с коэффициентом m является преобразованием подобия с коэффициентом .
Выберем ортонормированный репер (О, Е₁, Е₂, Е₃) так, чтобы точка О совпала с центром гомотетии. Если М (х, у, z)—произвольная точка пространства, а точка М’ (х′, у′, z′) — ее образ, то из формулы (1) получаем аналитическое выражение гомотетии в пространстве:
(3)

Пользуясь формулами (3), можно доказать, что гомотетия переводит плоскость (прямую), не проходящую через центр гомотетии, в параллельную плоскость (прямую), а плоскость (прямую), проходящую через центр гомотетии,— в себя. Аналогично, пользуясь формулой (2), убеждаемся в том, что гомотетия сохраняет простое отношение трех точек. Отсюда следует, что гомотетия переводит отрезок в отрезок, луч — в луч, полуплоскость — в полуплоскость и полупространство — в полупространство. Из формулы (2) следует также, что гомотетия переводит угол в равный ему угол.
Докажем, что гомотетия с коэффициентом m сохраняет ориентацию пространства, если , и меняет его ориентацию, если . Действительно, пусть (А, В, С, D) — произвольный репер, а (А′, В’, С’, D’) — его образ. По формуле (2) получаем: , , поэтому

Отсюда и следует сформулированное выше утверждение.

Теорема 1, сформулированная и доказанная (см. выше), полностью переносится на пространство, т. е. любое преобразование подобия пространства с коэффициентом является произведением гомотетии с тем же коэффициентом и произвольным центром на некоторое движение. Отсюда следует, что подобие пространства переводит плоскость (прямую) в плоскость (прямую), параллельные плоскости (прямые) —в параллельные плоскости (прямые). Подобие сохраняет простое отношение трех точек, поэтому оно переводит отрезок в отрезок, луч — в луч, полуплоскость — в полуплоскость, полупространство — в полупространство. Подобие переводит угол в равный ему угол, взаимно перпендикулярные прямые (плоскости) — во взаимно перпендикулярные прямые (плоскости).
Точно так же, как и на плоскости, можно доказать, что любое преобразование подобия либо сохраняет ориентацию пространства, либо меняет ее. В первом случае оно называется преобразованием подобия первого рода, а во втором случае — преобразованием подобия второго рода. Таким образом, гомотетия с положительным коэффициентом является преобразованием подобия первого рода, а гомотетия с отрицательным коэффициентом (в частности, центральная симметрия, ) — преобразованием подобия второго рода.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Применение геометрических преобразований к решению задач

Видео:Гомотетия. Коэффициент гомотетии. Центр гомотетии. Гомотетичные фигуры. Геометрия 8-9 классСкачать

ПРИМЕНЕНИЕ ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ К РЕШЕНИЮ ЗАДАЧ

Ученики 10 класса хорошо знакомы, а ученики 9 класса уже познакомились с такими геометрическими преобразованиями плоскости как поворот вокруг некоторой точки на заданный угол, параллельный перенос, осевая и центральная симметрии. Наша задача: сделать небольшой шаг за рамки школьного учебника и изучить еще несколько замечательных преобразований плоскости. Начнем мы с гомотетии.

Определение 1. Гомотетией с центром в точке М0 и коэффициентом k называется правило, по которому каждая точка М отображается в точку М’, и при этом выполняется условие:

(1).

Две фигуры назовем гомотетичными, если одна может быть получена и другой с помощью некоторой гомотетии.

Рассмотрим примеры гомотетии с различными коэффициентами.

На первом рисунке построен образ треугольника АВС при гомотетии с коэффициентом 2, а на втором – приведен пример гомотетии с коэффициентом -2. Наблюдательный читатель сразу заметит, что на обоих чертежах изображены пары подобных треугольников. Причем в обоих случаях коэффициент подобия равен 2. Кроме того, хорошо видно, что соответствующие стороны треугольника АВС и треугольника А’В’С’ – попарно параллельны.

Сформулируем основные свойства гомотетии.

Свойство 1. При гомотетии точка отображается в точку, отрезок в отрезок, а прямая в прямую.

Свойство 2. Гомотетия сохраняет принадлежность объектов (инцидентность). Другими словами, если точка принадлежит некоторой фигуре, то ее образ будет принадлежать образу этой фигуры, и наоборот.

Свойство 3. Гомотетия сохраняет параллельность. То есть, две параллельные прямые отображаются в две параллельные прямые.

Свойство 4. Гомотетия прямую отображает в параллельную ей прямую.

Рассмотрим важное следствие их этих свойств.

Следствие 1. Гомотетия любую фигуру отображает в подобную ей, причем коэффициент подобия равен модулю коэффициента гомотетии.

Доказательство. Достаточно показать, что это утверждение выполняется для треугольников. (Используем следующий признак подобия: два треугольника подобны, если соответственные углы у них равны.)

Равенство соответственных углов вытекает из свойства 4. Действительно, соответственные стороны исходного треугольника и его образа попарно параллельны, а это приводит к равенству углов.

Осталось доказать, что коэффициент подобия равен модулю коэффициента гомотетии. Рассмотрим чертеж на рисунке 3. Из определения гомотетии следует, что

(2).

Из этого, по свойству пропорциональных отрезков, следует, что АВ параллельна А’В’, откуда вытекает, что треугольники М0АВ и М0А’В’ подобны, так как у них пропорциональны длины сторон, прилежащих к общему (или вертикальным, если k