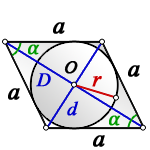
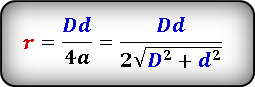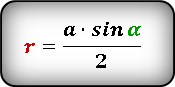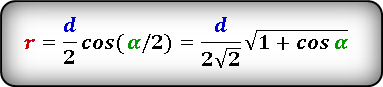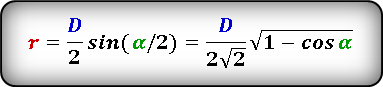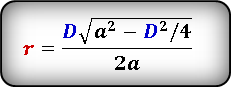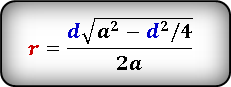1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол
a — сторона ромба
D — большая диагональ
d — меньшая диагональ
α — острый угол
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в ромб через диагонали ( r ) :
Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :
Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :
Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :
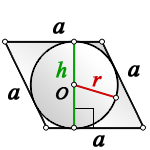
2. Радиус вписанной окружности ромба, равен половине его высоты
a — сторона ромба
h — высота
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в ромб ( r ) :
- Сторона ромба онлайн
- 1. Сторона ромба через высоту и площадь
- 2. Сторона ромба через высоту и угол
- 3. Сторона ромба через диагонали
- 4. Сторона ромба через угол и противолежащую диагональ
- 5. Сторона ромба через угол и диагональ из данного угла
- 6. Сторона ромба через площадь и радиус вписанной в ромб окружности
- 7. Сторона ромба через площадь и угол
- Ромб. Формулы, признаки и свойства ромба
- Признаки ромба
- Основные свойства ромба
- Сторона ромба
- Формулы определения длины стороны ромба:
- Диагонали ромба
- Формулы определения длины диагонали ромба:
- Периметр ромба
- Формула определения длины периметра ромба:
- Площадь ромба
- Формулы определения площади ромба:
- Окружность вписанная в ромб
- Формулы определения радиуса круга вписанного в ромб:
- 🌟 Видео
Видео:Задача 6 №27914 ЕГЭ по математике. Урок 132Скачать

Сторона ромба онлайн
С помощю этого онлайн калькулятора ромба можно найти длину стороны ромба по известным элементам. Для нахождения стороны ромба введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
| Открыть онлайн калькулятор |
Видео:Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать

1. Сторона ромба через высоту и площадь
Пусть известны площадь и высота ромба (Рис.1).
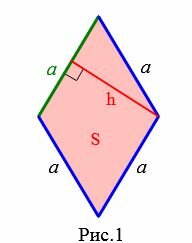 |
Покажем, что сторона ромба через высоту и площадь вычисляется формулой
| (small a=frac.) | (1) |
Формула площади ромба через сторону и высоту имеет следующий вид:
| (small S=a cdot h.) |
Откуда легко вывести формулу (1).
Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

2. Сторона ромба через высоту и угол
Рассмотрим ромб с высотой h и углом α между сторонами (Рис.2). Выведем формулу вычисления стороны ромба через высоту и угол.
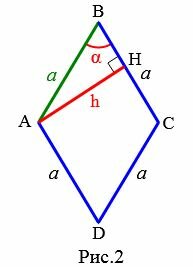 |
Для прямоугольного треугольника AHB применим теорему синусов:
| (small frac=frac.) |
Откуда получим формулу вычисления высоты ромба через сторону и угол между сторонами:
| (small a=frac.) | (2) |
Заметим, что формула (2) справедлива для любого угла ромба, как для острого, так и для тупого. Действительно. Из четвертого свойста ромба (см. статью Ромб) следует, что сумма соседних углов ромба равна 180°. Тогда для угла C можно записать: (small angle C=180°-alpha.) Следовательно (small sin angle C=sin(180°-alpha)=sin alpha.) Получили, что синусы углов ромба равны. Поэтому в качестве угла между сторонами ромба можно выбрать любой угол ромба.
Видео:Геометрия Угол ромба равен α, радиус вписанной окружности равен r. Найдите сторону и диагонали ромбаСкачать

3. Сторона ромба через диагонали
Выведем формулу вычисления сторон ромба через диагонали.
Выразим сторону a ромба через диагонали. Поскольку диагонали ромба перпендикулярны и делятся пополам точкой их пересечения (свойства 5 и 6 ромба), то диагонали делят ромб на четыре равных прямоугольных треугольника (Рис.3).
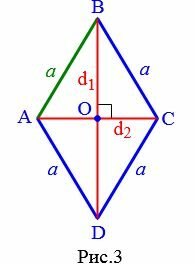 |
Применим к прямоугольному треугольнику AOB теорему Пифагора:
| (small a^2= left( frac right)^2+left( frac right)^2.) |
| (small a= frac<sqrt> ) | (3) |
Видео:Радиус вписанной в ромб окружности (6701)Скачать

4. Сторона ромба через угол и противолежащую диагональ
Пусть известны один из углов α=∠ABC ромба и противолежащая диагональ d=AC (Рис.4). Выведем формулу вычисления сторон ромба.
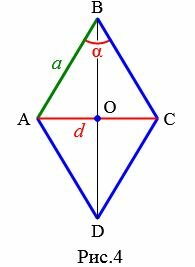 |
Проведем другой диагональ BD. Как было отмечено выше, диагонали ромба перпендикулярны и делятся пополам точкой их пересечения. Кроме этого, диагонали ромба делят углы ромба пополам. Применим теорему синусов для прямоугольного треугольника AOB:
| (small frac=frac<large frac><large sin frac>.) |
Откуда получим формулу стороны ромба через угол и противолежащую диагональ:
| (small a=frac<large 2 cdot sin frac>.) | (4) |
Формулу (4) можно записать и в другом виде, применяя формулу синуса половинного угла:
| (small sin frac=sqrt<frac>.) | (5) |
Подставляя (5) в (4), получим:
| (small a=frac<large 2 cdot sqrt<frac>>.) |
| (small a=large frac< sqrt>.) | (6) |
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

5. Сторона ромба через угол и диагональ из данного угла
Пусть известны один из углов α=∠ABC ромба и диагональ из данного угла d=BD (Рис.5). Выведем формулу вычисления высоты ромба.
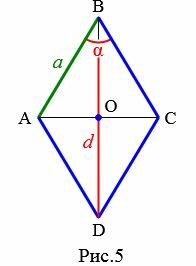 |
Проведем другой диагональ AC. Как было отмечено в выше, диагонали ромба перпендикулярны и делятся пополам точкой их пересечения. Для прямоугольного треугольника AOB, имеем:
| (small frac =cos angle ABO.) | (7) |
Учитывая, что ( small BO=frac) и ( small angle ABO=frac), формулу (13) можно записать так:
| (small frac< large frac >= cos frac .) |
| (small a=frac<large 2 cdot cos large frac>.) | (8) |
Формулу (8) можно записать и в другом виде, применяя формулу косинуса половинного угла:
| (small cos frac=sqrt<frac>.) | (9) |
Подставляя (9) в (8), получим:
| (small a=frac<large 2 cdot sqrt<frac>>.) |
| (small a=large frac< sqrt>.) | (10) |
Видео:ЕГЭ Математика Задание 6#27914Скачать
6. Сторона ромба через площадь и радиус вписанной в ромб окружности
В статье Площадь ромба показали, что площадь ромба через сторону и радиус вписанной в ромб окружности вычисляется формулой
| (small S= 2 cdot a cdot r.) | (11) |
Из формулы (11) получим:
| ( small a=frac ) | (12) |
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

7. Сторона ромба через площадь и угол
В статье Площадь ромба показали, что площадь ромба через сторону и угол вычисляется формулой
| (small S= a^2 cdot sin alpha.) | (13) |
Из формулы (13) найдем a:
| ( small a=frac ) | (14) |
Получили формулу сторон ромба через площадь и угол.
Видео:Геометрия, номера 45.1, 46.1 (радиус вписанной окружности)Скачать

Ромб. Формулы, признаки и свойства ромба
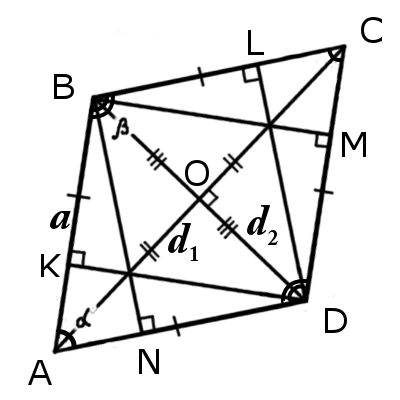 | 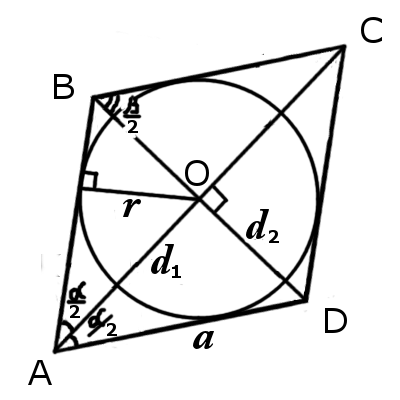 |
| Рис.1 | Рис.2 |
Видео:Площадь ромба. Легче понять...Скачать
Признаки ромба
∠BAC = ∠CAD или ∠BDA = ∠BDC
Δ ABO = Δ BCO = Δ CDO = Δ ADO
Видео:ЕГЭ Математика Задание 6#27913Скачать
Основные свойства ромба
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
AC 2 + BD 2 = 4AB 2
Видео:Радиус описанной окружностиСкачать

Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:
| a = | S |
| ha |
2. Формула стороны ромба через площадь и синус угла:
| a = | √ S |
| √ sinα |
| a = | √ S |
| √ sinβ |
3. Формула стороны ромба через площадь и радиус вписанной окружности:
| a = | S |
| 2 r |
4. Формула стороны ромба через две диагонали:
| a = | √ d 1 2 + d 2 2 |
| 2 |
5. Формула стороны ромба через диагональ и косинус острого угла ( cos α ) или косинус тупого угла ( cos β ):
| a = | d 1 |
| √ 2 + 2 cosα |
| a = | d 2 |
| √ 2 — 2 cosβ |
6. Формула стороны ромба через большую диагональ и половинный угол:
| a = | d 1 |
| 2 cos ( α /2) |
| a = | d 1 |
| 2 sin ( β /2) |
7. Формула стороны ромба через малую диагональ и половинный угол:
| a = | d 2 |
| 2 cos ( β /2) |
| a = | d 2 |
| 2 sin ( α /2) |
8. Формула стороны ромба через периметр:
| a = | Р |
| 4 |
Видео:Сможешь найти сторону ромба по радиусам окружностей?Скачать
Диагонали ромба
Формулы определения длины диагонали ромба:
d 1 = a √ 2 + 2 · cosα
d 1 = a √ 2 — 2 · cosβ
d 2 = a √ 2 + 2 · cosβ
d 2 = a √ 2 — 2 · cosα
d 1 = 2 a · cos ( α /2)
d 1 = 2 a · sin ( β /2)
d 2 = 2 a · sin ( α /2)
d 2 = 2 a · cos ( β /2)
7. Формулы диагоналей через площадь и другую диагональ:
| d 1 = | 2S |
| d 2 |
| d 2 = | 2S |
| d 1 |
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
| d 1 = | 2 r |
| sin ( α /2) |
| d 2 = | 2 r |
| sin ( β /2) |
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Периметр ромба
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Площадь ромба
Формулы определения площади ромба:
4. Формула площади ромба через две диагонали:
| S = | 1 | d 1 d 2 |
| 2 |
5. Формула площади ромба через синус угла и радиус вписанной окружности:
| S = | 4 r 2 |
| sinα |
6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):
| S = | 1 | d 1 2 · tg ( α /2) |
| 2 |
| S = | 1 | d 2 2 · tg ( β /2) |
| 2 |
Видео:Геометрия. ОГЭ по математике. Задание 16Скачать

Окружность вписанная в ромб
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
| r = | h |
| 2 |
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
| r = | S |
| 2 a |
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
| r = | √ S · sinα |
| 2 |
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
| r = | a · sinα |
| 2 |
| r = | a · sinβ |
| 2 |
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
| r = | d 1 · sin ( α /2) |
| 2 |
| r = | d 2 · sin ( β /2) |
| 2 |
6. Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d 1 · d 2 |
| 2√ d 1 2 + d 2 2 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
| r = | d 1 · d 2 |
| 4 a |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
🌟 Видео
Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

ЕГЭ математика 6#8🔴Скачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать