Как найти расстояние от прямой до окружности

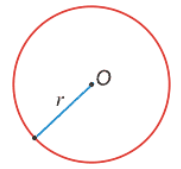
Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.

Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.

Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2

Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.

Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.

Квадрат касательной равен произведению секущей на ее внешнюю часть

Центральный угол — это угол, вершина которого совпадает с центром окружности.

Дугой называется часть окружности, заключенная между двумя точками.

Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.

Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.

Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.

Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.

Периметр сектора: P = s + 2R.

Площадь сектора: S = Rs/2 = ПR 2 а/360°.

Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.

Расстояние между двумя фигурами

Общее определение расстояния между двумя произвольными фигурами выходит за рамки школьной программы, и мы его не приводим. Ряд частных случаев, когда расстояние между двумя фигурами можно ввести на базе школьного материала, перечислен в следующей таблице.

Фигуры	Рисунок	Определение расстояния
Две точки		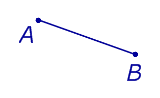Расстоянием между двумя точками называют длину отрезка AB.
Точка, лежащая на прямой		Расстояние равно 0.
Точка, не лежащая на прямой		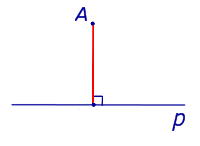Расстоянием от точки до прямой называют длину перпендикуляра, опущенного из точки на прямую.
Две параллельные прямые		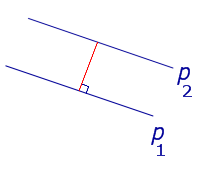Расстоянием между параллельными прямыми называют длину перпендикуляра, опущенного из любой точки одной прямой на другую прямую.
Две пересекающиеся прямые		Расстояние равно 0.
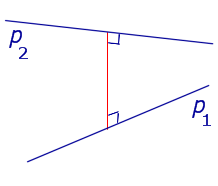
Две скрещивающиеся прямые		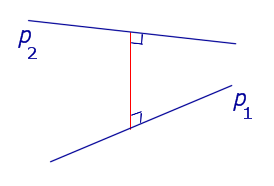Расстоянием между скрещивающимися прямыми называют длину общего перпендикуляра к этим прямым.
Точка, лежащая на плоскости		Расстояние равно 0.
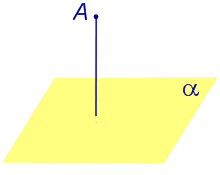
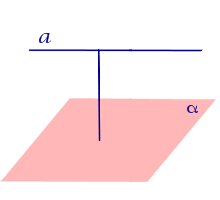
Точка, не лежащая на плоскости		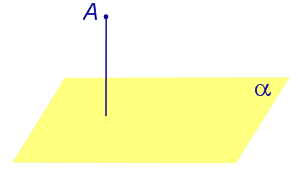Расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из этой точки на плоскость.
Прямая, пересекающая плоскость		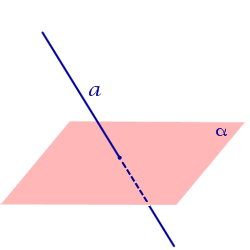Расстояние равно 0.
Прямая, лежащая на плоскости		Расстояние равно 0.
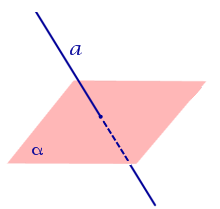
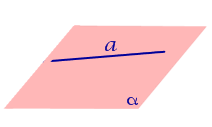
Прямая, параллельная плоскости		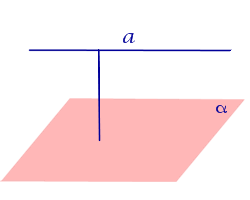Расстоянием от прямой, параллельной плоскости, до плоскости называют длину перпендикуляра, опущенного из любой точки данной прямой на плоскость.
Две пересекающиеся плоскости		Расстояние равно 0.
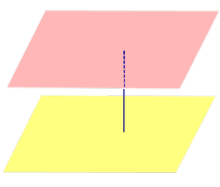
Две параллельные плоскости		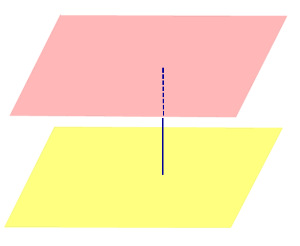Расстоянием между параллельными плоскостями называют длину перпендикуляра, опущенного из любой точки одной плоскости на другую плоскость (все такие перпендикуляры имеют одну и ту же длину).
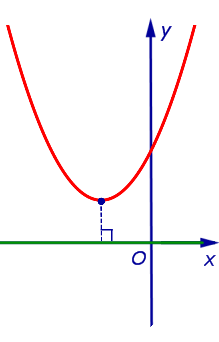
Парабола y = a x 2 + b x + c , не пересекающая ось абсцисс, и ось абсцисс		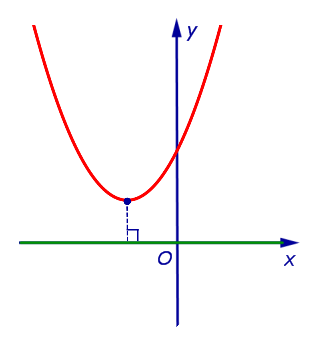Расстоянием от параболы, не пересекающей ось абсцисс, до оси абсцисс называют длину кратчайшего отрезка, один из концов которого лежит на параболе, а другой на оси абсцисс. Этим кратчайшим отрезком является перпендикуляр, опущенный из вершины параболы на ось абсцисс.
Окружность и не пересекающая ее прямая		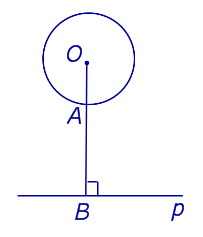Расстоянием между окружностью и непереcекающей ее прямой называют длину кратчайшего отрезка, один из концов которого лежит на окружности, а другой конец – на прямой. Если перпендикуляр OB , опущенный из центра O окружности на прямую, пересекает окружность в точке A, то расстояние от окружности до прямой равно длине отрезка AB.
Две непересекающиеся окружности, каждая из которых лежит вне другой		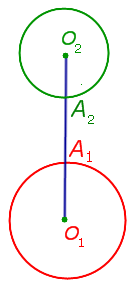Расстоянием между непересекающимися окружностями называют длину кратчайшего отрезка, один из концов которого лежит на одной окружности , а другой конец – на другой окружности. Если линия центров O1O2 пересекает окружность с центром O1 в точке A1, а окружность с центром O2 – в точке A2, то расстояние между окружностями будет равно длине отрезка A1A2.
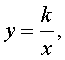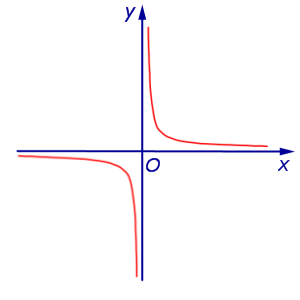Гипербола где k – любое, отличное от нуля, число, и ось абсцисс.		Расстояние между гиперболой и осью абсцисс считается равным 0, поскольку гипербола неограниченно приближается к оси абсцисс (длина отрезка, один из концов которого лежит на гиперболе, а другой конец – на оси абсцисс, может быть сколь угодно малой).

Две точки

Определение расстояния:
Расстоянием между двумя точками называют длину отрезка AB.

Точка, лежащая на прямой

Расстояние равно 0.

Точка, не лежащая на прямой

Определение расстояния:
Расстоянием от точки до прямой называют длину перпендикуляра, опущенного из точки на прямую.

Две параллельные прямые параллельные прямые

Определение расстояния:
Расстоянием между параллельными прямыми называют длину перпендикуляра, опущенного из любой точки одной прямой на другую прямую.

Две пересекающиеся прямые пересекающиеся прямые

Расстояние равно 0.

Определение расстояния:
Расстоянием между скрещивающимися прямыми называют длину общего перпендикуляра к этим прямым.

Точка, лежащая на плоскости

Расстояние равно 0.

Точка, не лежащая на плоскости

Определение расстояния:
Расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из этой точки на плоскость.

Расстояние равно 0.

Расстояние равно 0.

Определение расстояния:
Расстоянием от прямой, параллельной плоскости, до плоскости называют длину перпендикуляра, опущенного из любой точки данной прямой на плоскость.

Две пересекающиеся плоскости

Расстояние равно 0.

Две параллельные плоскости

Определение расстояния:
Расстоянием между параллельными плоскостями называют длину перпендикуляра, опущенного из любой точки одной плоскости на другую плоскость (все такие перпендикуляры имеют одну и ту же длину).

Парабола y = a x 2 + b x + c , не пересекающая ось абсцисс, и ось абсцисс

Определение расстояния:
Расстоянием от параболы, не пересекающей ось абсцисс, до оси абсцисс называют длину кратчайшего отрезка, один из концов которого лежит на параболе, а другой на оси абсцисс.
Этим кратчайшим отрезком является перпендикуляр, опущенный из вершины параболы на ось абсцисс.

Окружность и не пересекающая ее прямая

Определение расстояния:
Расстоянием между окружностью и непереcекающей ее прямой называют длину кратчайшего отрезка, один из концов которого лежит на окружности , а другой конец – на прямой.
Если перпендикуляр OB , опущенный из центра O окружности на прямую, пересекает окружность в точке A , то расстояние от окружности до прямой равно длине отрезка AB.

Две непересекающиеся окружности, каждая из которых лежит вне другой Две непересекающиеся окружности, каждая из которых лежит вне другой

Определение расстояния:
Расстоянием между непересекающимися окружностями называют длину кратчайшего отрезка, один из концов которого лежит на одной окружности, а другой конец – на другой окружности.
Если линия центров O₁O₂ пересекает окружность с центром O₁ в точке A₁, а окружность с центром O₂ – в точке A₂, то расстояние между окружностями будет равно длине отрезка A₁A₂.

Окружность

Вы будете перенаправлены на Автор24

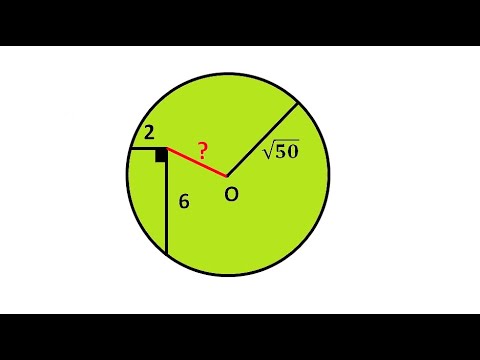
Определение окружности

Окружность — геометрическая фигура, состоящая из всех точек, расположенных на равном расстоянии от заданной точки.

В рамках определения 1, заданная точка называется центром окружности.

Отрезок, соединяющий центр окружности с любой ее точкой называется радиусом окружности $(r)$ (Рис. 1).

Рисунок 1. Окружность с центром в точке $O$ и радиусом $r$

Отрезок, соединяющий две любые точки окружности, называется хордой.

Хорда, проходящая через центр окружности, называется диаметром $(d)$.

Взаимное расположение прямой и окружности

Окружность имеет три возможных взаимных расположений относительно прямой:

Если расстояние от центра окружности до прямой меньше радиуса, то прямая имеет две точки пересечения с окружностью.

Если расстояние от центра окружности до прямой равно радиусу, то прямая имеет две точки пересечения с окружностью.

Если расстояние от центра окружности до прямой больше радиуса, то прямая имеет две точки пересечения с окружностью.

Уравнение окружности

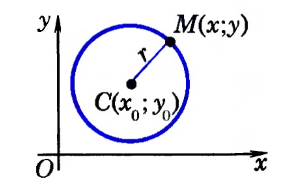
Выведем уравнение окружности в декартовой системе координат $xOy$. Пусть центр окружности $C$ имеет координаты $(x_0,y_0)$, а радиус окружности равен $r$. Пусть точка $M$ с координатами $(x,y)$ — произвольная точка этой окружности (рис. 2).

Рисунок 2. Окружность в декартовой системе координат

Готовые работы на аналогичную тему

Расстояние от центра окружности до точки $M$ вычисляется следующим образом

Но, так как $M$ лежит на окружности, то по определению 3, получаем $CM=r$. Тогда получим следующее

Уравнение (1) и есть уравнение окружности с центром в точке $(x_0,y_0)$ и радиусом $r$.

В частности, если центр окружности совпадает с началом координат. То уравнение окружности имеет вид

Длина окружности

Выведем формулу длины окружности $C$ через её радиус. Для этого рассмотрим две окружности с длинами $C$ и $C’$ и радиусами $R$ и $R’$. Впишем в ним правильные $n-угольники$ с периметрами $P$ и $P’$ и длинами сторон $a$ и $a’$ соответственно. Как нам известно, сторона вписанного -угольника равна

Неограниченно увеличивая количество сторон правильных многоугольников $n$ получим, что

Получили, что отношение длины окружности к её диаметру постоянное число для любой окружности. Эту константу принято обозначать числом $pi approx 3,14$. Таким образом, получим

Формула (2) и есть формула для вычисления длины окружности.

Пример задачи на понятие окружность

Найти уравнение окружности с центром в точке $(1, 2)$. Проходящей через начало координат и найти длину данной окружности.

Решение.

Найдем сначала уравнение данной окружности. Для этого будем использовать формулу (1). Так как центр окружности лежит в точке $(1, 2)$, получим

Найдем радиус окружности как расстояние от точки $(1, 2)$ до точки $(0,0)$

Получаем, уравнение окружности имеет вид:

Найдем длину окружности по формуле (2). Получим

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 29 03 2022

📽️ Видео