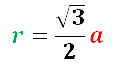Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны.
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
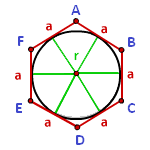
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
, где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне.
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
Ты нашел то, что искал? Поделись с друзьями!
. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Радиус такой окружности равен .
. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Радиус вписанной окружности в шестиугольник
По определению, правильным шестиугольником является выпуклый многоугольник с шестью вершинами и шестью равными сторонами и внутренними углами. Сумма его углов определяется, как произведение 180° на (n-2), при этом n — количество сторон, равное в данном случае 6. Соответственно, сумма углов составит 720° (180° х (6 — 2)), а величина внутреннего угла — 120°. В правильный шестиугольник можно легко вписать окружность. Стороны шестиугольника будут касательны к вписанной окружности. Центры правильного шестиугольника и вписанной окружности совпадают.
Радиус вписанной окружности рассчитывается по формуле:
а — сторона шестиугольника.
Т.е. радиус равняется половине корня из трех, умноженному на величину его стороны. В правильном 6-угольнике радиус R описанной окружности равняется его стороне. Следовательно, r вписанной окружности можно рассчитать, как половину корня из трех, умноженному на R описанной окружности.
Быстро и правильно рассчитать радиус вписанной в заданный 6-угольник окружности можно с помощью онлайн калькулятора.
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Нахождение радиуса вписанной в правильный многоугольник окружности
В публикации представлена формула, с помощью которой можно найти радиус окружности, вписанной в правильный многоугольник, а также приведен пример решения задачи для лучшего понимания представленного материала.
Видео:Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

Формула расчета радиуса окружности
На рисунке изображен правильный шестиугольник со вписанной в него окружностью, но формула ниже подходит для любого правильного n-угольника.
где a – длина стороны.
Примечание: зная радиус вписанного круга можно найти сторону равностороннего n-угольника:
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Пример задачи
Вычислите радиус вписанной в правильный восьмиугольник окружности, если длина его стороны составляет 12 см.
Решение:
Воспользуемся первой формулой, подставив в нее известное значение.
💡 Видео
Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать

Формулы радиусов описанной и вписанной окружностей правильного многоугольника 2Скачать

Радиус описанной окружностиСкачать

9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписаннойСкачать

Вариант 32, №8. Радиус окружности, вписанной в правильный шестиугольник. Длина окружности. ЗадачаСкачать

Геометрия 9 класс (Урок№22 - Формулы площади правильного многоугольника,стороны и радиуса впис.окр.)Скачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Задача 6 №27917 ЕГЭ по математике. Урок 134Скачать

Периметр правильного шестиугольника равен 150. Найдите диаметр описанной около него окружности (ЕГЭ)Скачать

9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Задача 6 №27910 ЕГЭ по математике. Урок 130Скачать

Площадь многоугольника через радиус вписанной окружностиСкачать

Свойства правильного шестиугольникаСкачать

найти радиус окружности, описанной вокруг треугольникаСкачать