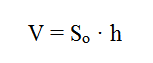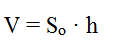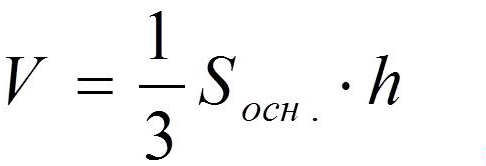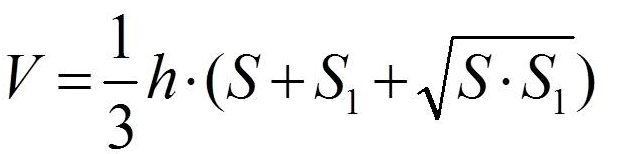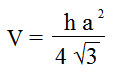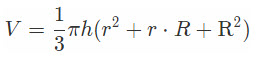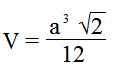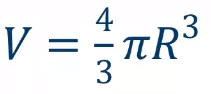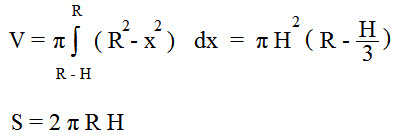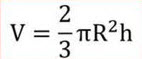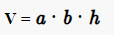Треугольник — это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
Формула расчета объема треугольника:
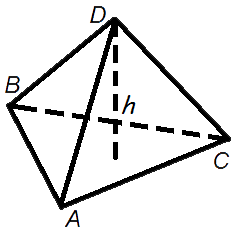
V — объем треугольника;
S — площадь треугольника;
h — толщина треугольника.
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета объема треугольника. С помощью этого онлайн калькулятора расчета объема треугольника вы сможете вычислить объем треугольника по площади и толщине.
- Формулы объема геометрических фигур
- Объем куба
- Объем призмы
- Объем параллелепипеда
- Объем прямоугольного параллелепипеда
- Объем пирамиды
- Объем правильного тетраэдра
- Объем цилиндра
- Объем конуса
- Объем шара
- Формулы вычисления объема всех геометрических фигур
- Все формулы объема геометрических тел
- Объем куба
- Объем призмы
- Объем параллелепипеда
- Объем пирамиды
- Объем усеченной пирамиды
- Объем цилиндра
- Объем правильной треугольной пирамиды
- Объем конуса
- Объем усеченного конуса
- Объем тетраэдра
- Объем шара
- Объем шарового сегмента и сектора
- Объем прямоугольного параллелепипеда
- 🎥 Видео
Видео:Математика 5 Объем Объем прямоугольного параллелепипедаСкачать

Формулы объема геометрических фигур
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Объем куба
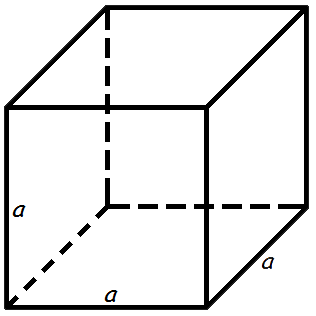
Объем куба равен кубу длины его грани.
Формула объема куба:
Видео:Площадь прямоугольного треугольника. Как найти площадь прямоугольного треугольника?Скачать

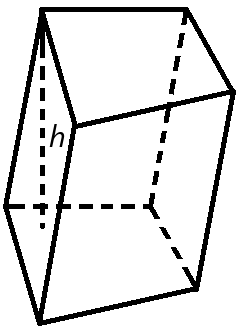
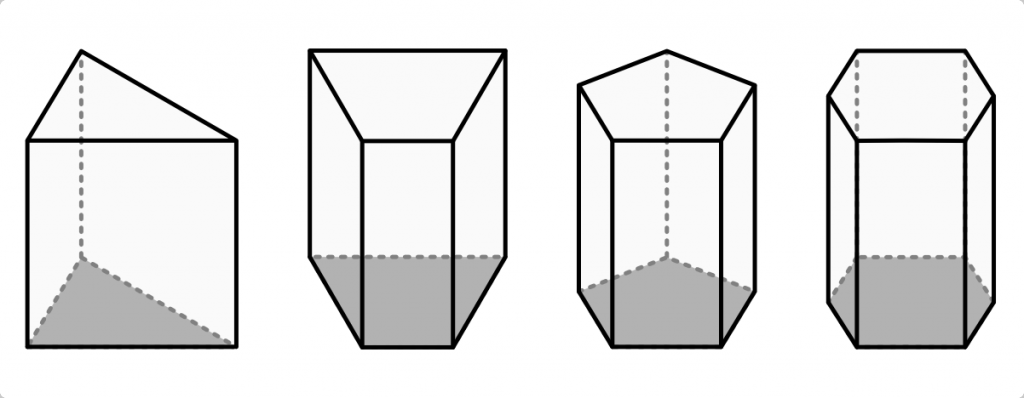
Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы:
Видео:Как найти площадь треугольника без формулы?Скачать

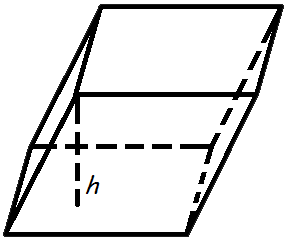
Объем параллелепипеда
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда:
Видео:Формула объёма прямоугольного параллелепипеда (для 3В)Скачать

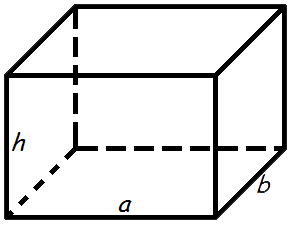
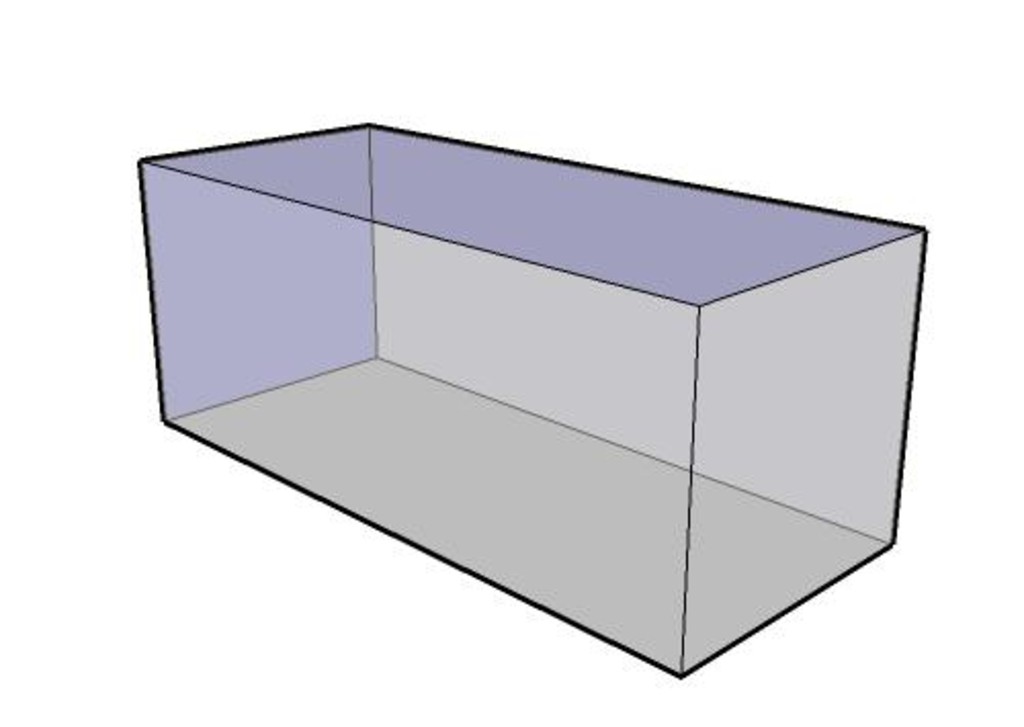
Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда:
Видео:5 класс, 21 урок, Объемы. Объем прямоугольного параллелепипедаСкачать

Объем пирамиды
Объем пирамиды равен трети от произведения площади ее основания на высоту.
Формула объема пирамиды:
| V = | 1 | So · h |
| 3 |
Видео:Математика | Объём в жизни и в математикеСкачать

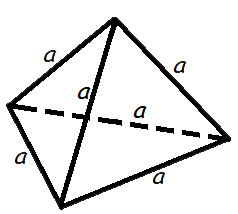
Объем правильного тетраэдра
Формула объема правильного тетраэдра:
| V = | a 3 √ 2 |
| 12 |
Видео:КАК НАЙТИ ОБЪЕМ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА? Примеры | МАТЕМАТИКА 5 классСкачать

Объем цилиндра
Объем цилиндра равен произведению площади его основания на высоту.
Формулы объема цилиндра:
Видео:Как найти объем. Принцип Кавальери | Ботай со мной #050 | Борис Трушин |Скачать

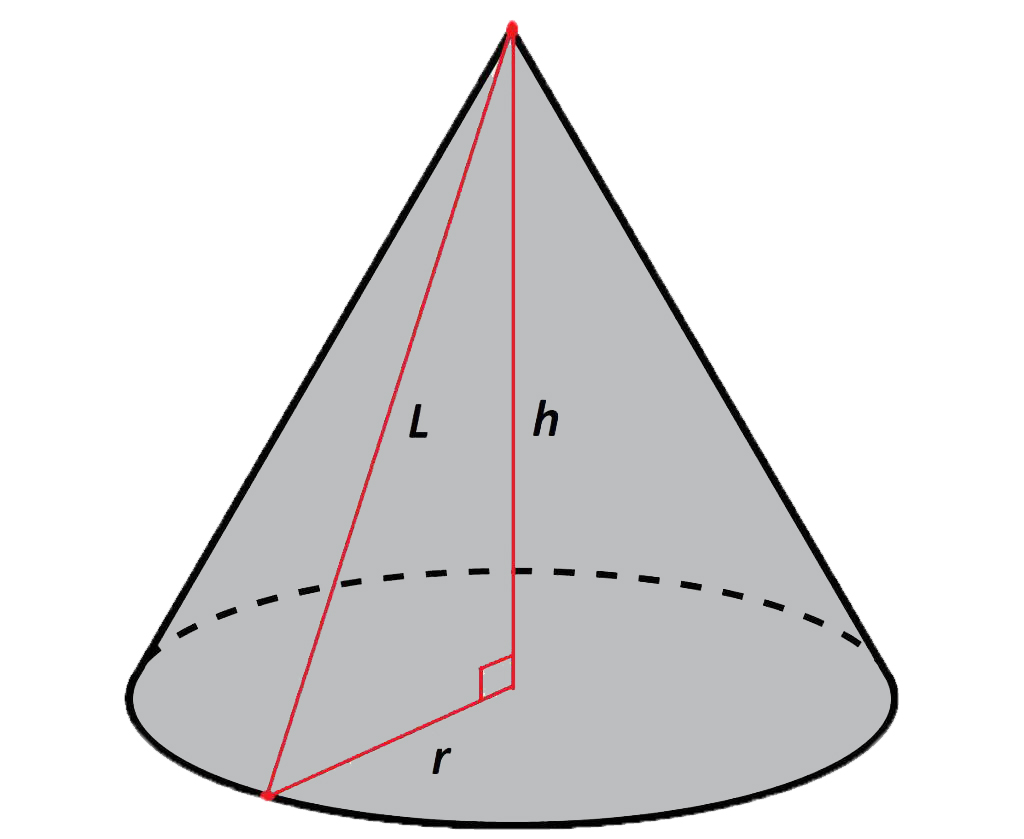
Объем конуса
Объем конуса равен трети от произведению площади его основания на высоту.
Формулы объема конуса:
| V = | 1 | π R 2 h |
| 3 |
| V = | 1 | So h |
| 3 |
Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

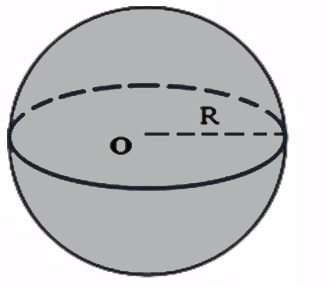
Объем шара
Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.
Формула объема шара:
| V = | 4 | π R 3 |
| 3 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Площадь прямоугольника. Как найти площадь прямоугольника?Скачать

Формулы вычисления объема всех геометрических фигур
Объём — это аддитивная функция от множества (мера), характеризующая вместимость области пространства, которую оно занимает. Изначально возникло и применялось без строгого определения в отношении тел трёхмерного евклидова пространства. Первые точные определения были даны Пеано (1887) и Жорданом (1892). Впоследствии понятие было обобщено Лебегом на более широкий класс множеств.
Для определения объёма существует несколько существенно различных подходов, которые дополняют друг друга и согласованы по конечному результату на «хороших множествах». Обычно под понятием объёма понимается мера Жордана, но иногда мера Лебега. Для римановых многообразий понятие объёма вводится аналогично понятию площади поверхности.
Видео:КАК НАЙТИ ПЛОЩАДЬ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА? Примеры | МАТЕМАТИКА 5 классСкачать

Все формулы объема геометрических тел
Объем куба
Объем куба равен кубу длины его грани.
Формула объема куба:
V — объем куба,
a — длина грани куба.
Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы:
V- объем призмы,
So — площадь основания призмы,
h — высота призмы.
Объем параллелепипеда
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда:
V- объем параллелепипеда,
So — площадь основания,
h — длина высоты.
Объем пирамиды
Объем пирамиды равен одной трети произведения площади основания S (ABCDE) на высоту h (OS).
V — объем пирамиды,
So — площадь основания пирамиды,
h — длина высоты пирамиды.
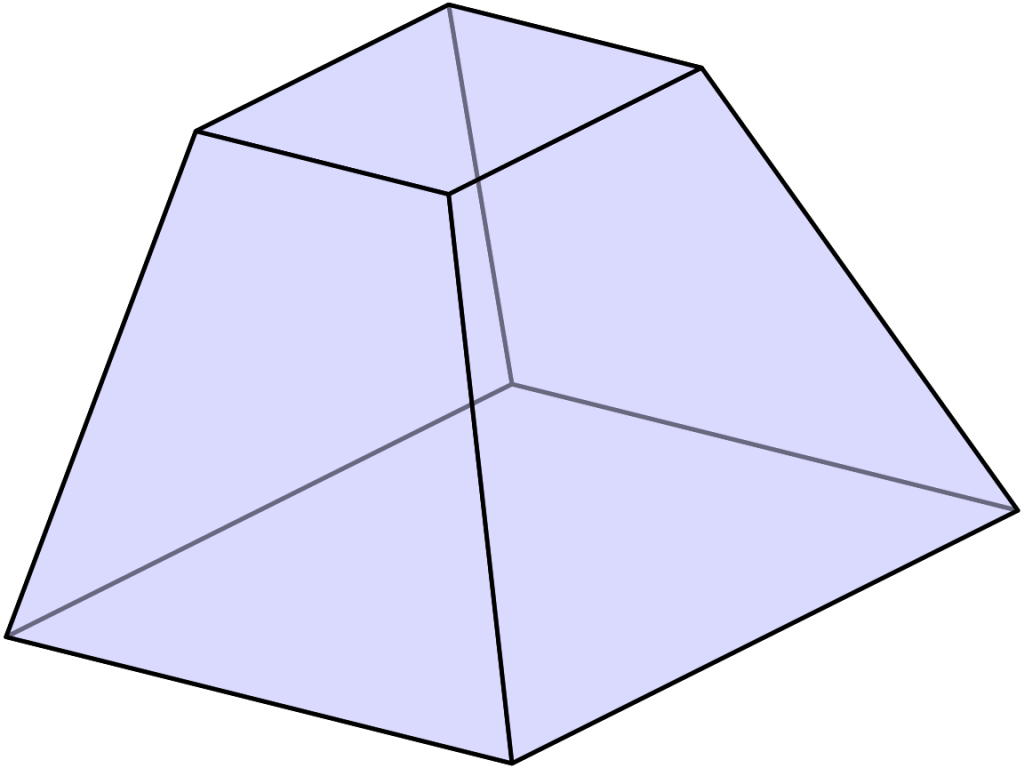
Объем усеченной пирамиды
Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S1(abcde), нижнего основания усеченной пирамиды S2 (ABCDE) и средней пропорциональной между ними.
Формула объема усеченной пирамиды:
S1 — площадь верхнего основания усеченной пирамиды,
S2 — площадь нижнего основания усеченной пирамиды,
h — высота усеченной пирамиды.
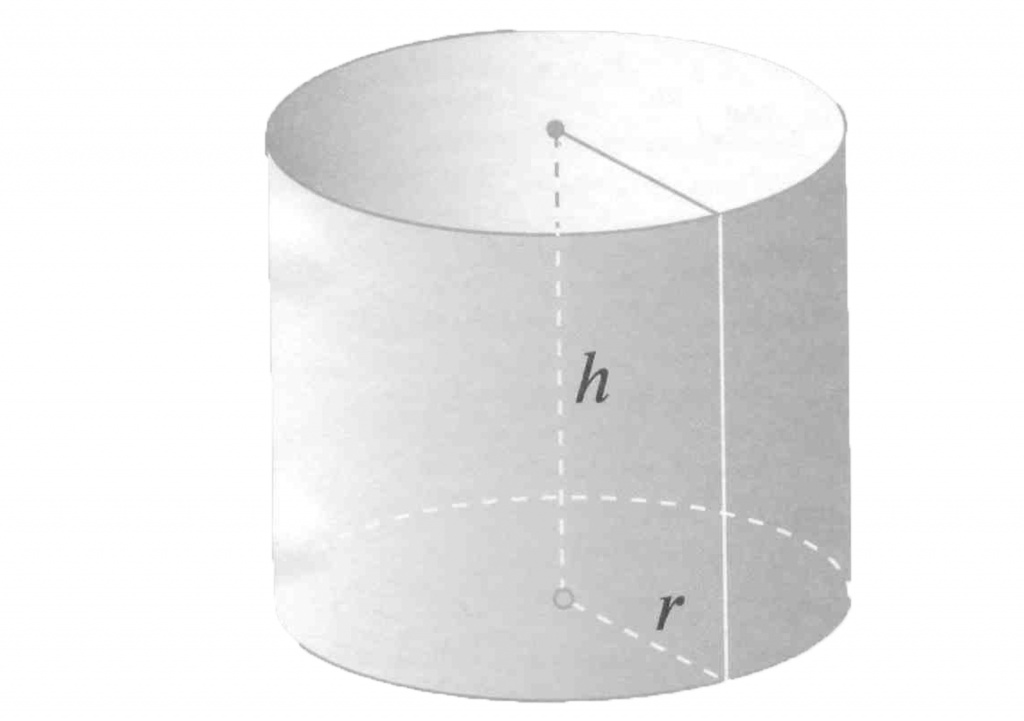
Объем цилиндра
Объем цилиндра равен произведению площади его основания на высоту.
V — объем цилиндра,
So — площадь основания цилиндра,
R — радиус цилиндра,
h — высота цилиндра,
π = 3.141592
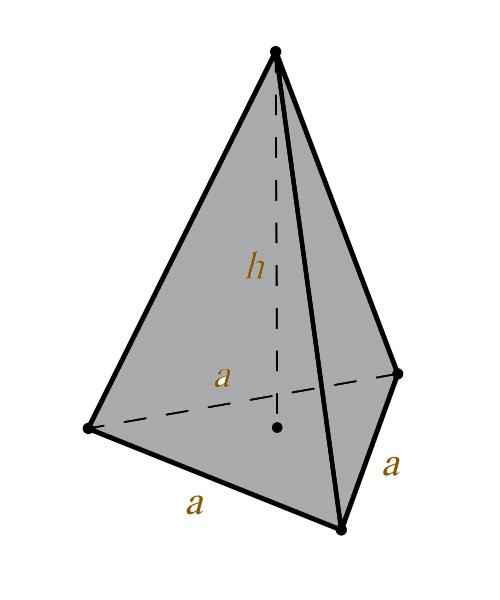
Объем правильной треугольной пирамиды
Формула объема правильной треугольной пирамиды:
V — объем пирамиды;
h — высота пирамиды;
a — сторона основания пирамиды.
Объем конуса
Объем круглого конуса равен трети произведения площади основания S на высоту H.
V — объем конуса;
R — радиус основания;
H — высота конуса;
I — длина образующей;
S — площадь боковой поверхности конуса.
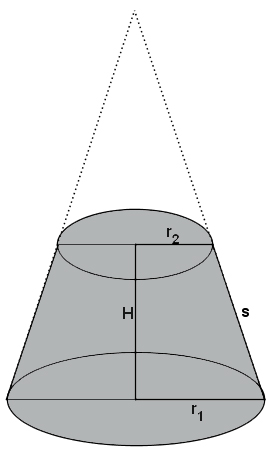
Объем усеченного конуса
Объем усеченного конуса равен разности объемов двух полных конусов.
Формула объема усеченного конуса:
V — объем усеченного конуса;
H — высота усеченного конуса;
R и R 2 — радиусы нижнего и верхнего оснований.
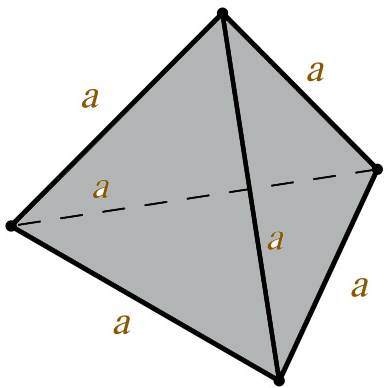
Объем тетраэдра
Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.
V — объем тетраэдра;
a — ребро тетраэдра.
Объем шара
Объем шара равен четырем третьим от его радиуса в кубе перемноженного на число пи.
V — объем шара;
R — радиус шара;
S — площадь сферы.
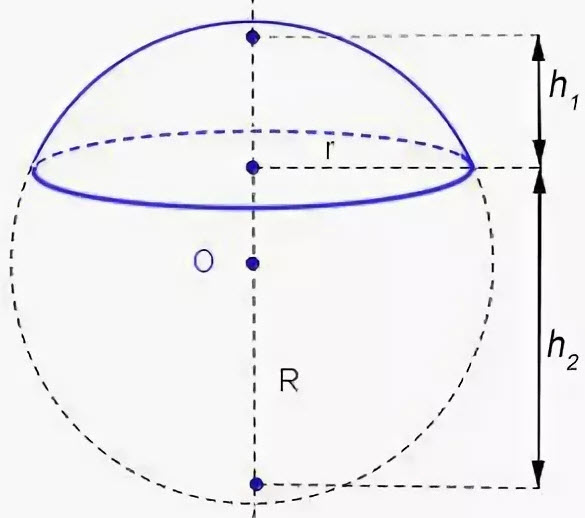
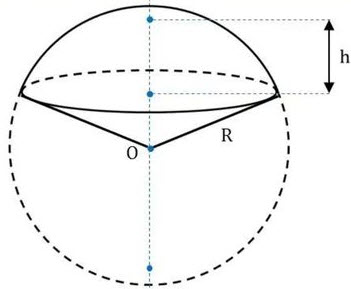
Объем шарового сегмента и сектора
Шаровый сегмент — это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.
Формула объема шарового сегмента:
R — радиус шара
H — высота сегмента
π ≈ 3,14
Формула объема шарового сектора:
h — высота сегмента
R — радиус шара
π ≈ 3,14
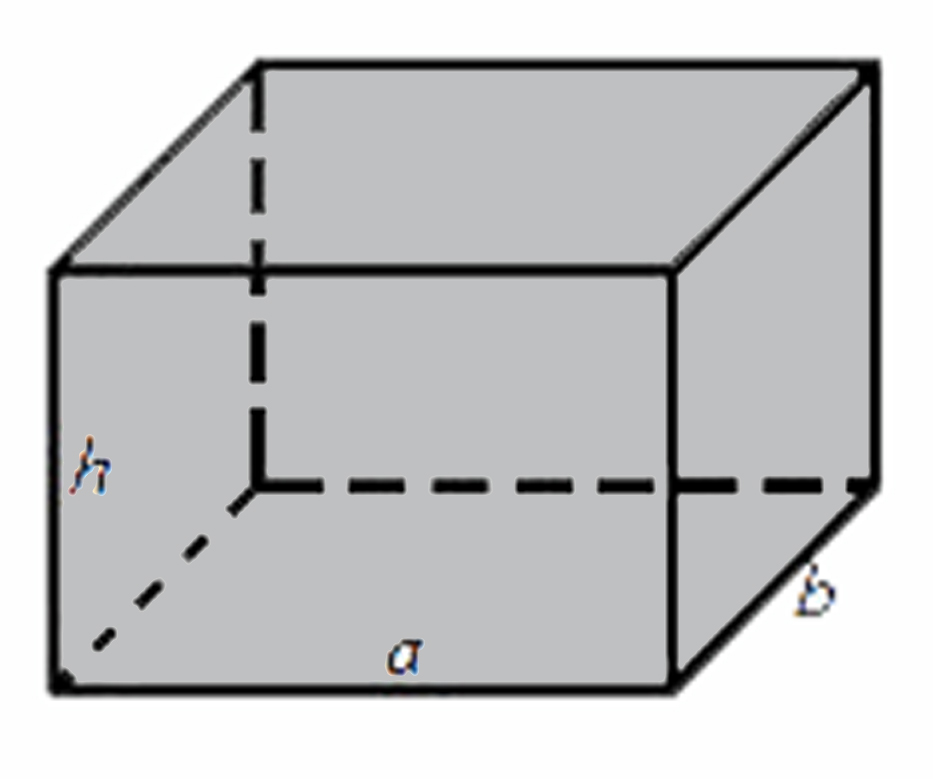
Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда:
V — объем прямоугольного параллелепипеда,
a — длина,
b — ширина,
h — высота.
🎥 Видео
КАК НАЙТИ ВЫСОТУ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА, ЕСЛИ ИЗВЕСТЕН ОБЪЕМ И ПЛОЩАДЬ ОСНОВАНИЯ? 5 классСкачать

КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать

Математика 5 класс (Урок№32 - Объём прямоугольного параллелепипеда. Единицы объёма.)Скачать

Площади фигур. Сохраняй и запоминай!#shortsСкачать

Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

Объем прямоугольного параллелепипеда и кубаСкачать

Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Найдите объем треугольной призмыСкачать