В данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала.
- Определение медианы треугольника
- Свойства медианы
- Свойство 1 (основное)
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Примеры задач
- Треугольник. Формулы и свойства треугольников.
- Типы треугольников
- По величине углов
- По числу равных сторон
- Вершины углы и стороны треугольника
- Свойства углов и сторон треугольника
- Теорема синусов
- Теорема косинусов
- Теорема о проекциях
- Формулы для вычисления длин сторон треугольника
- Медианы треугольника
- Свойства медиан треугольника:
- Формулы медиан треугольника
- Биссектрисы треугольника
- Свойства биссектрис треугольника:
- Формулы биссектрис треугольника
- Высоты треугольника
- Свойства высот треугольника
- Формулы высот треугольника
- Окружность вписанная в треугольник
- Свойства окружности вписанной в треугольник
- Формулы радиуса окружности вписанной в треугольник
- Окружность описанная вокруг треугольника
- Свойства окружности описанной вокруг треугольника
- Формулы радиуса окружности описанной вокруг треугольника
- Связь между вписанной и описанной окружностями треугольника
- Средняя линия треугольника
- Свойства средней линии треугольника
- Периметр треугольника
- Формулы площади треугольника
- Формула Герона
- Равенство треугольников
- Признаки равенства треугольников
- Первый признак равенства треугольников — по двум сторонам и углу между ними
- Второй признак равенства треугольников — по стороне и двум прилежащим углам
- Третий признак равенства треугольников — по трем сторонам
- Подобие треугольников
- Признаки подобия треугольников
- Первый признак подобия треугольников
- Второй признак подобия треугольников
- Третий признак подобия треугольников
- Решение треугольников онлайн
- Решение треугольника по трем сторонам
- Решение треугольника по двум сторонам и углу между ними
- Решение треугольника по стороне и любым двум углам
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Определение медианы треугольника
Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.
Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).
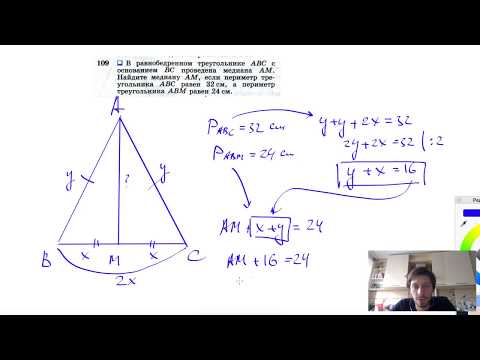
Видео:№109. В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найдите медиану AMСкачать
Свойства медианы
Свойство 1 (основное)
Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.
В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:
Свойство 2
Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.
Свойство 3
Три медианы делят треугольник на 6 равновеликих треугольников.
Свойство 4
Наименьшая медиана соответствует большей стороне треугольника, и наоборот.
- AC – самая длинная сторона, следовательно, медиана BF – самая короткая.
- AB – самая короткая сторона, следовательно, медиана CD – самая длинная.
Свойство 5
Допустим, известны все стороны треугольника (примем их за a, b и c).
Длину медианы ma, проведенную к стороне a, можно найти по формуле:
Видео:№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать

Примеры задач
Задание 1
Площадь одной из фигур, образованной в результате пересечения трех медиан в треугольнике, равняется 5 см 2 . Найдите площадь треугольника.
Решение
Согласно свойству 3, рассмотренному выше, в результате пересечения трех медиан образуются 6 треугольников, равных по площади. Следовательно:
S△ = 5 см 2 ⋅ 6 = 30 см 2 .
Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.
Решение
Воспользуемся формулой, приведенной в свойстве 5:
Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Треугольник. Формулы и свойства треугольников.
Видео:Уравнения стороны треугольника и медианыСкачать

Типы треугольников
По величине углов
По числу равных сторон
Видео:Построение медианы в треугольникеСкачать

Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β , тогда a > b
если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 — 2 bc · cos α
b 2 = a 2 + c 2 — 2 ac · cos β
c 2 = a 2 + b 2 — 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Видео:Построение биссектрисы в треугольникеСкачать

Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 1 2 √ 2 b 2 +2 c 2 — a 2
mb = 1 2 √ 2 a 2 +2 c 2 — b 2
mc = 1 2 √ 2 a 2 +2 b 2 — c 2
Видео:Вычисляем высоту через координаты вершин 1Скачать

Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√ bcp ( p — a ) b + c
lb = 2√ acp ( p — b ) a + c
lc = 2√ abp ( p — c ) a + b
где p = a + b + c 2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Видео:Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )
Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Связь между вписанной и описанной окружностями треугольника
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Видео:500 ДНЕЙ НА ОСТРОВЕ ХАРДКОР МАЙНКРАФТ ВСЕ СЕРИИСкачать
Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Видео:ПОП ИТ ТРЕЙДЫ! ЧелленджСкачать

Формулы площади треугольника
Формула Герона
| S = | a · b · с |
| 4R |
Видео:Длина медианы треугольникаСкачать

Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
Видео:Геометрия В треугольнике ABC известно, что AC = a, AB = BC = b, AM и CK – биссектрисы треугольникаСкачать

Подобие треугольников
∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k ,
где k — коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:ОГЭ 23 КАК РЕШИТЬ ЗАДАЧУ НА ПОДОБНЫЕ ТРЕУГОЛЬНИКИСкачать

Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Видео:ОГЭ Р-2 номер 16Скачать

Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем 
 |
 |
 |
 | (1) |
 | (2) |
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения
 . . |
Пример 1. Известны стороны треугольника ABC: 

Решение. Из формул (1) и (2) находим:
  . . |
  . . |
 , ,  . . |
И, наконец, находим угол C:
  |
Видео:№231. Медиана AM треугольника ABC равна половине стороны ВС. Докажите, что треугольникСкачать

Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
 |
Найдем сторону c используя теорему косинусов:
 . . |
 . . |
Далее, из формулы
 . . |
 . . | (3) |
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:
 . . |
Пример 2. Известны две стороны треугольника ABC: 

Решение. Иcпользуя теорму косинусов найдем сторону c:
 , , |
   . . |
Из формулы (3) найдем cosA:
  |
 . . |
Поскольку уже нам известны два угла то находим третий:
  . . |
Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
 |
Так как, уже известны два угла, то можно найти третий:
 . . |
Далее, для находждения сторон b и c воспользуемся тероемой синусов:
 , ,  . . |
 , ,  . . |
Пример 3. Известна одна сторона треугольника ABC: 

Решение. Поскольку известны два угла, то легко можно найти третий угол С:
  |
Найдем сторону b. Из теоремы синусов имеем:
 |
 |
Найдем сторону с. Из теоремы синусов имеем:




















