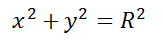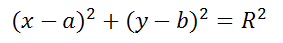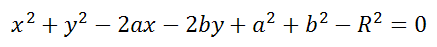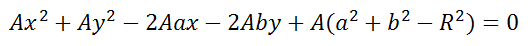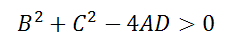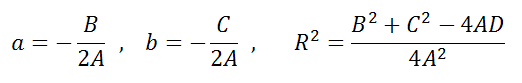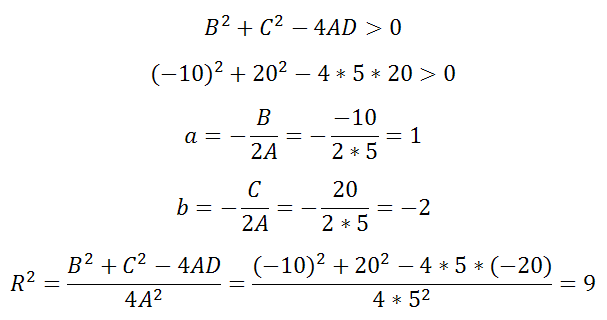Как нарисовать окружность на оси координат

Числовая ось

Прямоугольная декартова система координат на плоскости

Формула для расстояния между двумя точками координатной плоскости

Уравнение окружности на координатной плоскости

Видео:Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

Числовая ось

Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Видео:Тригонометрическая окружность. Как выучить?Скачать

Прямоугольная декартова система координат на плоскости

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA₁ и AA₂ на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A₁ на числовой оси Ox , ординатой точки A называют координату точки A₂ на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.

Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .

Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.

Видео:КАК НАРИСОВАТЬ КРУГ В ИЗОМЕТРИИ (ОВАЛ В ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ).Скачать

Формула для расстояния между двумя точками координатной плоскости

Утверждение 1 . Расстояние между двумя точками координатной плоскости

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.

что и требовалось доказать.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Уравнение окружности на координатной плоскости

Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:

Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A₀ (x₀ ; y₀) .

Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид

Видео:ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

Как нарисовать окружность по координатам

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Как построить окружность?

Как построить окружность?

Окружностью называется фигура которая состоит из всех точек плоскости равноудаленных от данной точки. Эта точка называется центром окружности.

Радиусом называется любой отрезок соединяющей точку окружности с ее центром.

Чтобы построить окружность необходимо знать уравнение окружности:

(х – а) 2 + (у – b) 2 = R 2

Точка С(а;b) центр окружности, радиус R, х и у – координаты произвольной точки окружности.

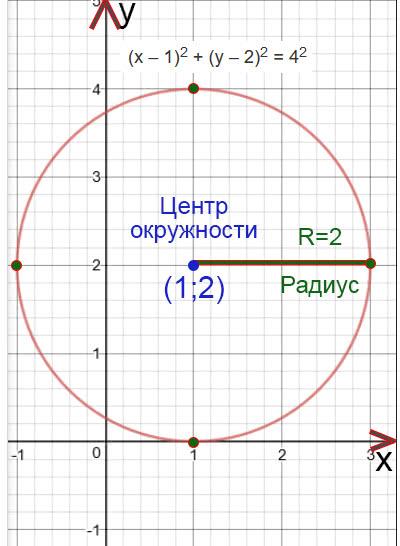
И так, чтобы построить окружность необходимо знать цент окружности и радиус. Рассмотрим пример:

Пример №1:
(х – 1) 2 + (у – 2) 2 = 4 2

Найдем центр окружности:
х – 1=0
x=1

Центр окружности будет находится в точке (1;2)

Найдем радиус окружности:
R 2 =4
R 2 =2 2
R=2

Построим окружность. Отметим сначала центр окружности, а потом отложим с четырех сторон (вверх, вниз, влево и право) длину радиуса и отметим эту длину точками. Потом проведем окружность.

Пример №2:
х 2 + (у + 1) 2 =1

Можно представить уравнение окружности ввиде:
(х-0) 2 + (у + 1) 2 =1 2

Найдем центр окружности:
х=0

Центр окружности будет находится в точке (0;–1)

Найдем радиус окружности:
R 2 =1
R 2 =1 2
R=1

Построим окружность.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Видео:Как начертить окружность без циркуля? #ShortsСкачать

Алгоритм генерации круга

Рисование круга на экране немного сложнее, чем рисование линии. Существует два популярных алгоритма для генерации круга — алгоритм Брезенхема и алгоритм средней точки круга . Эти алгоритмы основаны на идее определения последующих точек, необходимых для рисования круга. Давайте обсудим алгоритмы подробно —

Уравнение окружности: X 2 + Y 2 = r 2 , где r — радиус.

Видео:Уравнение окружности (1)Скачать

Алгоритм Брезенхема

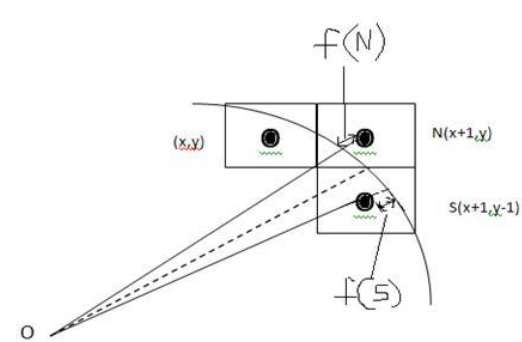
Мы не можем отобразить непрерывную дугу на растровом дисплее. Вместо этого мы должны выбрать ближайшее положение пикселя, чтобы завершить дугу.

На следующем рисунке вы можете видеть, что мы поместили пиксель в положение (X, Y) и теперь должны решить, куда поместить следующий пиксель — в N (X + 1, Y) или в S (X + 1, Y-1).

Это может быть решено параметром решения d .

• Если d
• Если d> 0, то S (X + 1, Y-1) должен быть выбран в качестве следующего пикселя.

Алгоритм

Шаг 1 — Получить координаты центра окружности и радиуса и сохранить их в x, y и R соответственно. Установите P = 0 и Q = R.

Шаг 2 — Установите параметр решения D = 3 — 2R.

Шаг 3 — Повторите шаг 8, пока P ≤ Q.

Видео:Построение проекции вектора на осьСкачать

Окружность на координатной плоскости

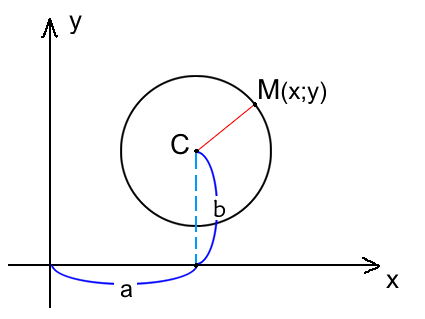
Окружность на плоскости — это множество точек на плоскости равноудаленных от точки центра. На рисунке данная точка обозначена C.

Видео:Система координат · Ось абсцисс и ось ординат · Координатная плоскость Урок Математики для 6 классаСкачать

Окружность радиуса R с центром в начале координат представляется уравнением:

Окружность радиуса R с центром в точке C(a;b) представляется уравнением:

Расстояние от центра окружности С(a;b) до точки M(x;y) называется радиусом окружности R (на рисунке красная линия ).
Это уравнение можно записать в виде:

Если уравнение помножить на любое число A, то получим

Примечание
Окружность относится к линии второго порядка, так как представляется уравнением второй степени.

Необходимые условия для этого:
1. Отсутствие в уравнение второй степени члена с произведением xy;
2. Коэффициенты при x 2 и y 2 были равны в уравнение вида:

3. Если выполняется неравенство

Видео:Контрольное упражнение 1. Сетка осей.Скачать

Как найти радиус и центр окружности

Уравнение Ax 2 +Bx+Ay 2 +Cy+D=0 если оно удовлетворяет примечаниям (1, 2 и 3), то тогда (a;b) и радиус R окружности можно найти по формулам:

Пример 1
Уравнение 5x 2 -10x+5y 2 +20y-20=0
Здесь
A=5, B=-10, C=20, D=-20
Оно удовлетворяет примечаниям 1, 2 и выполняется неравенство

Решая, получаем что центр есть (1;-2), а радиус R=3

Анимационный график окружности

Пример 2
Уравнение второй степени x 2 +4xy+y 2 =1 не является окружностью, так как в нём есть член 4xy.

Пример 3
Уравнение второй степени 4x 2 +9y 2 =36 не представляет окружность, так как в нём коэффициенты при x 2 и y 2 не равны.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.3 / 5. Количество оценок: 4

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Рисунки и фигуры по координатам

Программа «Рисуем по координатам» является хорошим наглядным инструментом для создания (построения) рисунков и фигур по координатам на координатной плоскости (сетке). Все точки рисунка (картинки) наносятся по координатам в порядке их следования. После чего соединяем линией точки. В результате получится заданный рисунок (фигура) на координатной плоскости по координатам.

Программа «Рисуем по координатам» предназначена для рисования разной сложности рисунков (легкие, простые, сложные). и построения различных фигур по координатам точек на координатной плоскости и подойдет для 4, 5, 6 классов. Она позволяет наглядно увидеть, как можно использовать математику для построения (рисования) различных рисунков (картинок); животные, птицы, цветы, листья, деревья, машины, самолеты, ракеты, грибы, пауки, корабли, змеи, рыбки и другие.

Видео:Как найти координаты точек на тригонометрической окружностиСкачать

СБОРНИК РИСУНКОВ И ФИГУР ПО КООРДИНАТАМ

В сборнике представлены рисунки и фигуры по координатам на клетчатом поле (сетке) в прямоугольной системе координат, где принято, что единичный отрезок 1 клетка. Для удобства выбора задания по возрасту, по способности и познавательным интересом, все задания представлены различного уровня сложности (легкие, простые, сложные) и имеют разную тематику. Можно научиться и самому создавать любой рисунок по координатам. Все готовые рисунки и картинки по координатам можно бесплатно и без регистрации скачать и распечатать на листе формата А4.

Рисование по координатам точек на координатной плоскости (сетке) это не только увлекательное занятие, но и поучительное как в области рисования, так и в математике. Программа «Рисуем по координатам» предназначена для использования, как на уроках математики, так и для организации интересного досуга дома. Саму же программу можно бесплатно скачать здесь.

Существует и другой способ создать рисунок (фигуру) по координатам не в программе «Рисуем по координатам», а на клетчатом поле. Данная тема интересна тем, что в координатной плоскости на клетчатом поле можно строить не только различные графики функций, но и увидеть связь природной красоты и строгой математики, создавая красивые рисунки и фигуры по координатам своими руками.

КАК РИСОВАТЬ ПО КООРДИНАТАМ

Рисунки и фигуры на координатной плоскости строятся по точкам. Каждая точка на плоскости имеет две координаты и записывается в виде двух чисел X (икс) и Y (игрек) через точку с запятой в скобках, например точка A (х; у), где первая цифра обозначает расстояние, отложенное от центра системы координат по оси X (икс), вторая цифра расстояние, отложенное от центра по оси Y (игрек). Рассмотрим построение координатных точек на координатной плоскости (сетке) на реальном примере.

Для этого нужно взять либо обычный лист из тетради в клеточку, либо распечатать готовый лист А4 в клетку его можно скачать здесь. Создаём прямоугольную систему координат. Для этого, рисуем координатные оси X и Y, где принимаем за единичный отрезок 1 клетку и для удобства нумеруем цифрами, как показано на рисунке. Можно распечатать уже готовый лист А4 в клетку с осями координат и с числами здесь. . Вот теперь все готово и можно приступать.

Возьмем для примера первую координату точку A (2;5) нашего рисунка или картинки и отложим эти расстояния по координатным осям X и Y. Первое число 2 мы отложим по оси X, а второе значение нашей координаты число 5 по координатной оси Y. В пересечении двух мысленно проведенных перпендикулярных линий к осям координат (они обозначены пунктирной линией на рисунке), мы получим нашу первую точку A (2;5).

Таким же методом строим координаты второй точки, третьей и так далее. После построения всех точек мы соединяем прямой линией первую точку со второй, вторую с последующей точкой в порядке их следования. После соединения всех точек мы получим заданный рисунок (фигуру) по своим координатам.

Чтобы найти координаты любой точки рисунка (фигуры) на плоскости, необходимо создать координатную плоскость на этом рисунке и опустить из этой точки перпендикуляры на координатные оси X и Y. Эти два значения и будут ее координаты.

РИСУНКИ ПО КООРДИНАТАМ ДЛЯ НАЧИНАЮЩИХ

В сборнике представлены различные рисунки на координатной плоскости с координатами для разного возраста. Рисунки (фигуры) по координатам для начинающих были построены или взяты из различных источников: журналов, интернет-ресурсов. Данный материал можно использовать как карточки с заданиями с целью закрепления материала. Все рисунки (фигуры) по координатам можно бесплатно и без регистрации скачать в формате pdf и распечатать на листе формата А4. Лист А4 в клетку или координатные сетки при необходимости можно скачать здесь.

ЛЕГКИЕ РИСУНКИ

ПРОСТЫЕ РИСУНКИ

СРЕДНИЕ РИСУНКИ

РИСУНКИ ПО КООРДИНАТАМ СЛОЖНЫЕ И КРАСИВЫЕ

В сборнике представлены красивые и сложные рисунки на координатной плоскости с координатами для разных возрастных групп. Все красивые рисунки (картинки) по координатам после построения можно еще и раскрашивать красками, карандашами и фломастерами. Красивые и сложные рисунки по координатам показывают, что можно совершенствовать линии контура рисунков и реализовывать свои фантазии безгранично. Лист А4 в клетку и координатные сетки при необходимости можно скачать здесь.

СОБАКИ

КООРДИНАТЫ ДЛЯ РИСУНКОВ

В сборнике представлены различные примеры наборов координат без рисунка, по которым надо восстановить рисунок. Для этого необходимо на чистом листе в клетку востановить по координатам исходный рисунок. Представленные наборы имеют разную сложность и будут интересны для разных возрастных групп. Любой материал можно бесплатно и без регистрации скачать в формате pdf и распечатать на листе формата А4. Лист А4 в клетку при необходимости можно скачать здесь.

ЛЕГКИЕ РИСУНКИ

ПРОСТЫЕ РИСУНКИ

СЛОЖНЫЕ РИСУНКИ

ДОРИСУЙ ВТОРУЮ ПОЛОВИНУ

В сборнике дорисуй вторую половину, все картинки представляют собой незаконченный симметричный рисунок, выполненный на клетчатом поле с одной стороны оси. Необходимо дорисовывать вторую половину рисунка соблюдая симметрию. Дорисуй вторую половину начинать рисовать надо от простых рисунков по клеткам к более сложным. Данное задания развивает зрительное восприятие, произвольное внимание, пространственное мышление, усидчивость и внимание к деталям, а также тренирует мелкую моторику и координацию движений руки. Лист А4 в клетку при необходимости можно скачать здесь.

ПРОСТЫЕ РИСУНКИ

СЛОЖНЫЕ РИСУНКИ

ПОВТОРИ КРАСИВЫЕ РИСУНКИ ПО ОБРАЗЦУ

В сборнике красивые рисунки по образцу, представлены различные примеры рисунков без координат на клетчатом поле для разных возрастных групп. Можно повторить рисунок по образцу на чистом листе А4 в клетку, а можно добавить оси координат и перевести рисунок в координаты. Все красивые рисунки по образцу можно дорабатывать и фантазировать под свой вкус. Любой красивый рисунок по образцу можно бесплатно и без регистрации скачать в формате pdf и распечатать на листе формата А4. Лист А4 в клетку или координатные сетки при необходимости можно скачать здесь.

КРАСИВЫЕ РИСУНКИ

МАШИНЫ

КАРТОЧКИ РИСУНКОВ

В сборнике карточки рисунков представлены разные рисунки и фигуры различной сложности. В карточках можно либо повторить рисунок рядом на чистом поле в клетку, либо написать координаты этого рисунка. Данный материал можно использовать как учебные карточки для закрепления пройденного материала, самостоятельных работ и различных конкурсов и викторин. Все карточки сборников рисунков по координатам можно бесплатно и без регистрации скачать в формате pdf и распечатать на листе формата А4. Лист А4 в клетку или координатные сетки при необходимости можно скачать здесь.

СБОРНИК

ДОРИСУЙ РИСУНКИ ПО ОБРАЗЦУ

В сборнике рисунки по образцу представлены примеры рисунков различной сложности, которые можно либо дорисовать рисунок по образцу, либо рядом на чистом листе в клетку нарисовать его полностью глядя на образец. Дорисуй рисунки по образцу подойдут для использования разного возраста. Все рисунки по образцу можно бесплатно и без регистрации скачать в формате pdf и распечатать на листе формата А4. Лист А4 в клетку или координатные сетки при необходимости можно скачать здесь.

ЛЕГКИЕ РИСУНКИ (СБОРНИКИ)

ПРОСТЫЕ РИСУНКИ

НАРИСУЙ КАРТИНКИ ПО КЛЕТКАМ И РАСКРАСЬ

В сборнике нарисуй картинки по клеткам и раскрась, представлены как отдельные картинки, так и примеры сборников рисунков различной сложности, которые можно перерисовать по образцу на чистом листе в клетку, а при желании и раскрасить. Картинки по клеткам будут интересны для разного возраста. Любые рисунки (картинки) по клеткам можно бесплатно и без регистрации скачать в формате pdf и распечатать на листе формата А4. Лист А4 в клетку или координатные сетки при необходимости можно скачать здесь.

ПРОСТЫЕ РИСУНКИ

РИСУНКИ (СБОРНИКИ)

ЛИСТ А4 В КЛЕТКУ. МИЛЛИМЕТРОВКА А4

Чистый лист А4 в клетку, координатная сетка для печати или миллиметровая бумага может понадобиться при рисования рисунков по координатам, картинок по образцу и других видов работ. Все пустые листы в клетку и миллиметровки расположены на листе формата A4 и их можно свободно скачать. Листы в клетку представлены; в темную клетку (черная), светлую клетку (серая), с осями координат и с числами. Листы миллиметровой бумаги представлены в 4-х вариантах; blue (синяя), green (зеленая), orange (оранжевая), pink (розовая).

ВОЗМОЖНОСТИ ПРОГРАММЫ

Программа «Рисуем по координатам» имеет два режима:

1. Рисует на доске изображение по введенной Вами таблице точек координат, печатает в цвете таблицу и рисунок;
2. Составит таблицу координат по нарисованному на доске изображению.

• максимальный объем таблицы 255 строк;
• точность записи рисунка — 0,5 единиц по обеим осям;
• индикатором и переключателем режима работы — таблица /доска является значок наверху справа;
• вводите в ячейках таблицы координаты точек Х и У, начало ломаной линии — обозначайте значком + в третьей колонке;
• маленький квадрат, к примеру, глаз щенка обозначайте точкой в третьем столбце таблицы;
• строки таблицы, которые следует удалить, обозначьте знаком — в третьем столбце;
• в таблице не должно быть пустых или непонятных программе строк;
• по мере заполнения таблицы проверяйте, что получается, нажимая кнопку «Нарисовать» (F4);
• для поиска ошибок двигаетесь по таблице клавишами с вертикальными стрелками, на доске отрезок, соответствующий текущей строке таблицы, окрасится в красный цвет;
• рисовать на доске отрезки надо, удерживая кнопку мыши;
• кнопками справа можно изменять масштаб рисунка, сдвигать окно по доске;
• печать осуществляется принтером, способным обеспечить плотность печати (dpi) 300 точек на дюйм. Тогда на листе А4 во всю его ширину будет рисунок затем таблица, по форме, принятой в газете «Математика..».

Загрузите примеры рисунков или скачайте с моего сайта и попробуйте дорисовать в них что-нибудь, или изобразите самостоятельно какой-нибудь домик, Вы увидите, как это здорово.

Этот сборник заданий поможет не только любому учителю организовать творческий подход к изучению данной темы, но и получить хорошие результаты в её усвоении.

Я надеюсь, что эти задания будут пользоваться спросом у учеников и учителей. Их можно применять как на уроках математики при изучении темы «Координатная плоскость», так и на занятиях кружка и факультатива.

🎥 Видео

Как начертить овал. Эллипс вписанный в ромбСкачать

Уравнение окружности ? Окружность в системе координат / Функция окружностиСкачать

начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Построение кривой в полярной системе координатСкачать

Тригонометрическая окружность для непонимающихСкачать