Как начертить окружность радиусом 20 см

Как быстро и просто рисовать круги разного диаметра

Умение рисовать ровные круги на поверхности может стать очень полезным в хозяйстве, особенно во время ремонта или для всевозможных поделок.

Чтобы нарисовать круг ровно, совсем необязательно использовать специальные инструменты

Как быстро нарисовать ровный круг без специальных инструментов

Существует масса способов рисовать круги без специальных инструментов, этот самый простой из них. Для его реализации вам нужно подготовить:

• пару карандашей;
• рулетку или линейку;
• полоску гофрированного картона (его можно вырезать из любой упаковочной коробки).

Когда все необходимое будет под рукой, можно приступать к действиям.

Иллюстрация	Инструкция к действиям
	Шаг 1. Подготовьте картон Первым делом вам следует подготовить полосу гофрированного картона. Ее длина должна на несколько сантиметров превышать радиус необходимого вам круга. Если гофрированного картона под рукой не оказалось, возьмите другую плотную бумагу.
	Шаг 2. Создайте отверстия С одной стороны картонной полоски (в паре сантиметров от края) проделайте отверстие под карандаш. Отступите от него подходящую вам длину, и создайте второе отверстие.
	Шаг 3. Нарисуйте круг Вставьте по карандашу в подготовленные отверстия. У вас получится своеобразный циркуль, которым удобно начертить ровный круг. Чтобы изменить размер круга, достаточно лишь проделать другое отверстие на картоне.

Всего за пару минут вы сможете нарисовать идеально ровный круг с любым диаметром

Как видите, этот способ не только простой и быстрый, он также не требует от вас никаких особых инструментов. Ведь кусок картона и пара карандашей найдутся в любом доме.

Круг. Окружность (центр, радиус, диаметр)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Данный урок посвящён изучению окружности и круга. Также учитель научит отличать замкнутые и незамкнутые линии. Вы познакомитесь с основными свойствами окружности: центром, радиусом и диаметром. Выучите их определения. Научитесь определять радиус, если известен диаметр, и наоборот.

Радиус — что это такое и как найти радиус окружности

Через длину стороны

Формула для нахождения длины окружности через радиус:

, где r — радиус окружности.

Найти радиус круга, зная окружность

Окружность круга PРезультат

Радиус и диаметр

Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.

А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:

Диаметр – это отрезок, который проходит через центр окружности и соединяет две противоположные точки на ее поверхности. По аналогии с радиусом под диаметром подразумевают и длину этого отрезка.

Обозначается диаметр также первой буквой своего слова – D или d.

Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.

Длина диаметра равна удвоенной длине радиуса.

Вычисление радиуса

Радиус можно посчитать разными способами.

Если известен диаметр

Этот способ самый простой. Диаметр равен двум радиусам. Поэтому радиус будет высчитываться по формуле r=d/2.

Если известна длина окружности круга

Также несложно будет узнать радиус, если известна длина окружности круга. Формула для расчета длины окружности C=2πr, в которой C является длиной окружности, π=3,14, а r — это как раз искомый радиус.

Преобразовав данную формулу, получим: r=C/2π. Вообще, число «Пи» в формуле — это постоянное значение, округленное до 3,14. На самом деле «Пи» выглядит так:

Означает данное значение отношение длины окружности к диаметру той же окружности.

Если известна площадь круга

Формула площади круга выглядит так: A= π(r²). Эту формулу можно преобразовать в формулу радиуса:

В ней A — это площадь круга, число «Пи» мы уже знаем, оно равно округленно 3,14, а r — это и есть искомое значение радиуса.

Как найти радиус круга, все школьники учат на геометрии. Взрослые, конечно, со временем забывают эти формулы. Но, прочитав данную статью, радиус круга может найти каждый: и взрослый, и ребенок.

Способ расчета радиуса круга:

Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга).
Формула радиуса круга:
где P – длина окружности, pi – число π, равное примерно 3.14

Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга).
Формула радиуса круга:
где S – площадь круга, pi – число π, равное примерно 3.14

Через сторону описанного квадрата

Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.

• r — искомый радиус окружности.
• a — сторона описанного квадрата.

Как посчитать радиус зная длину окружности

Чему равен радиус (r) если длина окружности C?

Формула

r = C /_2π , где π ≈ 3.14

Свойства радиуса

В отношении радиуса действуют несколько важных правил:

1. Радиус составляет половину диаметра. Это мы продемонстрировали только что.
2. У окружности может быть сколько угодно радиусов. Но все они будут равны по длине между собой.

Радиус, который перпендикулярен хорде, делит ее на две равные части.

Напомним, хордой называется любой отрезок, который проходит через две точки на поверхности окружности, но не через центр. Этим она принципиально отличается от диаметра.

По площади сектора и центральному углу

• Например, если площадь сектора равна 50 см 2 , а центральный угол равен 120 градусов, формула запишется следующим образом: .

Площадь сегмента

Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла .

Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах , получаем

В случае, когда величина α выражена в в радианах , получаем

Формулы для площади круга и его частей

Числовая характеристика	Рисунок	Формула
Площадь круга

,

где R – радиус круга, D – диаметр круга

Площадь сектора

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Площадь сегмента

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Площадь круга

,

где R – радиус круга, D – диаметр круга

Площадь сектора

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Площадь сегмента

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Центральный угол, вписанный угол и их свойства

Связанные определения

• Центральный угол в окружности — это угол , образованный двумя радиусами.
• Радиус кривизны кривой — это радиус окружности, имеющей с этой кривой касание второго порядка.

Примеры задач

Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.

Решение:
Используем первую формулу (через периметр):

Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .

Решение:
Воспользуемся формулой, выраженной через площадь фигуры:

Длина дуги

Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла .

В случае, когда величина α выражена в градусах , справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах , справедлива пропорция

из которой вытекает равенство:

Уравнение окружности

r 2 = ( x – a ) 2 + ( y – b ) 2

3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами ( a, b ) в декартовой системе координат:

Как быстро и просто рисовать круги разного диаметра

Умение рисовать ровные круги на поверхности может стать очень полезным в хозяйстве, особенно во время ремонта или для всевозможных поделок.

Чтобы нарисовать круг ровно, совсем необязательно использовать специальные инструменты

Как быстро нарисовать ровный круг без специальных инструментов

Существует масса способов рисовать круги без специальных инструментов, этот самый простой из них. Для его реализации вам нужно подготовить:

• пару карандашей;
• рулетку или линейку;
• полоску гофрированного картона (его можно вырезать из любой упаковочной коробки).

Когда все необходимое будет под рукой, можно приступать к действиям.

Иллюстрация	Инструкция к действиям
	Шаг 1. Подготовьте картон Первым делом вам следует подготовить полосу гофрированного картона. Ее длина должна на несколько сантиметров превышать радиус необходимого вам круга. Если гофрированного картона под рукой не оказалось, возьмите другую плотную бумагу.
	Шаг 2. Создайте отверстия С одной стороны картонной полоски (в паре сантиметров от края) проделайте отверстие под карандаш. Отступите от него подходящую вам длину, и создайте второе отверстие.
	Шаг 3. Нарисуйте круг Вставьте по карандашу в подготовленные отверстия. У вас получится своеобразный циркуль, которым удобно начертить ровный круг. Чтобы изменить размер круга, достаточно лишь проделать другое отверстие на картоне.

Всего за пару минут вы сможете нарисовать идеально ровный круг с любым диаметром

Как видите, этот способ не только простой и быстрый, он также не требует от вас никаких особых инструментов. Ведь кусок картона и пара карандашей найдутся в любом доме.

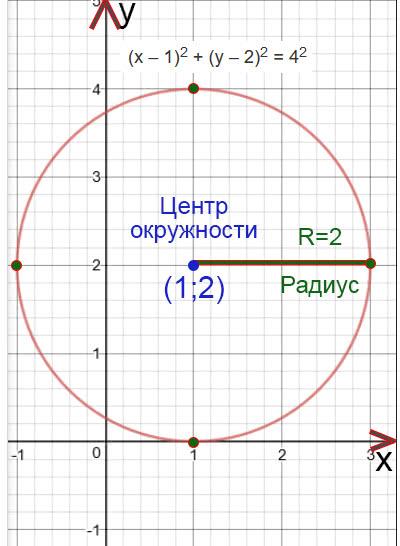
Как построить окружность?

Как построить окружность?

Окружностью называется фигура которая состоит из всех точек плоскости равноудаленных от данной точки. Эта точка называется центром окружности.

Радиусом называется любой отрезок соединяющей точку окружности с ее центром.

Чтобы построить окружность необходимо знать уравнение окружности:

(х – а) 2 + (у – b) 2 = R 2

Точка С(а;b) центр окружности, радиус R, х и у – координаты произвольной точки окружности.

И так, чтобы построить окружность необходимо знать цент окружности и радиус. Рассмотрим пример:

Пример №1:
(х – 1) 2 + (у – 2) 2 = 4 2

Найдем центр окружности:
х – 1=0
x=1

Центр окружности будет находится в точке (1;2)

Найдем радиус окружности:
R 2 =4
R 2 =2 2
R=2

Построим окружность. Отметим сначала центр окружности, а потом отложим с четырех сторон (вверх, вниз, влево и право) длину радиуса и отметим эту длину точками. Потом проведем окружность.

Пример №2:
х 2 + (у + 1) 2 =1

Можно представить уравнение окружности ввиде:
(х-0) 2 + (у + 1) 2 =1 2

Найдем центр окружности:
х=0

Центр окружности будет находится в точке (0;–1)

Найдем радиус окружности:
R 2 =1
R 2 =1 2
R=1

Построим окружность.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.