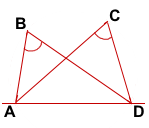
Признак принадлежности четырёх точек одной окружности
Если точки B и C лежат в одной полуплоскости относительно прямой AD, и точки B и C видны из отрезка AD под одним углом (то есть ∠ABD=∠ACD), то точки A, B, C и D лежат на одной окружности.
Дано: точки B и C лежат в одной полуплоскости относительно прямой AD,
Доказать: точки A, B, C, D лежат на одной окружности
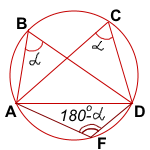
Опишем около треугольника ABD окружность.
Отметим на этой окружности произвольную точку F, лежащую относительно прямой AD в другой полуплоскости, чем точки B и C.
Четырёхугольник ABDF — вписанный в окружность. Следовательно, сумма его противолежащих углов равна 180°:
Рассмотрим четырехугольник ACDF.
Отсюда следует, что четырёхугольник ABDF — вписанный.
Поскольку около треугольника ABD можно описать только одну окружность, то точка C лежит на той же окружности, что и точки A, B и D.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

—> Сайт Манаенко Татьяны Викторовны —>
—>
| ЕГЭ [4] |
| ГИА [0] |
| Полезная информация [3] |
| Это интересно! [2] |
| Классное руководство в 6Б классе [2] |
—>
Видео:Доказать, что точки лежат на одной окружностиСкачать

Каталог статей
Признаки принадлежности точек окружности
Признак 1. Если в четырехугольнике ÐABC+ÐADC=180°, то около четырехугольника можно описать окружность.
Признак 2. Если ÐDAC=ÐDBC, то A, B, C, D лежат на одной окружности.
Признак 4. Если A, B, C, D – образы точек, лежащих на окружности, при движении, гомотетии или подобии.
Движение – преобразование плоскости, сохраняющее расстояние (перемещение).
Признак 5. Если A, B, C, D – образы точек, лежащих на прямой, при инверсии, причем эта прямая не проходит через центр инверсии.
Инверсия относительно окружности (O, r) или просто инверсия — преобразование множества всех точек плоскости без одной точки O, где O – центр окружности радиуса r. Каждой точке этого множества поставим в соответствие точку M’ так, чтобы она лежала на луче OM и OM·OM’=r 2 .
Окружность (O, r) называется окружностью инверсии, точка O — центром инверсии, r 2 – степенью инверсии
Теорема. Прямая, проходящая через центр O инверсии (без точки O), переходит в себя, а прямая, не проходящая через центр инверсии, переходит в окружность, проходящую через центр инверсии.
Признак 6. Теорема, обратная теореме Птолемея. Если сумма произведений длин противоположных сторон четырехугольника равна произведению длин его диагоналей, то четырехугольник можно вписать в окружность.
Видео:Четыре точки на окружности | ЕГЭ-2017. Задание 16. Математика. Профильный уровень| Борис ТрушинСкачать

Метод вспомогательной окружности. 9-й класс
Разделы: Математика
Класс: 9
Один мудрец сказал “ Высшее проявление духа – это разум, Высшее проявление разума – это геометрия, Клетка геометрии – треугольник. Он так же неисчерпаем, как и Вселенная. Окружность – душа геометрии. Познайте окружность, и вы не только познаете душу геометрии, но и возвысите душу свою”.
Рассмотрим один из основных геометрических методов решения задач – метод вспомогательной окружности. Предлагаю набор задач, который поможет понять и разобраться в этом методе.
При решении некоторых задач может оказаться полезной следующая теорема.
Т.1 Если для четырех точек плоскости А, В, М, К выполняется одно из следующих условий:
а) точки М и К расположены по одну сторону от прямой АВ и при этом 0 , то точки А, В, М, К расположены на окружности с диаметром АВ. (Это свойство вписанных углов сформулированное в более удобном виде для решения задач) Сформулированные выше предложения можно назвать свойства четырех точек окружности.
Т1 и Т2 и свойства вписанных углов позволяют решать некоторые интересные геометрические задачи с помощью метода, который называют методом вспомогательной окружности.
Суть метода проиллюстрируем на решении следующих задач.
В треугольнике АВС проведена высота СК. Найти длину отрезка, соединяющего точку К с серединой АС, если АС = 10см.
Проведем высоту АМ, тогда углы АКВ и АМВ равны по 90 0 , значит точки А, К, М, В лежат на одной окружности и АВ – диаметр.(На рисунке окружность изображена штриховой линией, хотя ее можно и вообще не изображать, а “представлять в уме”) Точка О – середина АС по условию
Следовательно, АО = ОВ = КО = r = 5 см. (рис. 3)

Рис. 3
В выпуклом четырехугольнике АВСD диагонали АС и ВD пересекаются в точке О.
0 , 0 , 0 . Найти углы САD и АDС.

Рис. 4
0 – 49 0 = 62 0 .Таким образом В и С лежат по одну сторону от АD и углы АВО и АСD равны значит точки А, В, С, D лежат на одной окружности. 0 , отсюда 0 – 111 0 = 69 0 .
2. дуга АDС равна 222 0 . Значит дуга DС равна 222 0 – 124 0 = 98 0 . Угол САD вписанный и равен 49 0 . Ответ: 0 0
В окружности проведены параллельные хорды АВ, FC, ED известно, что AD ∩ CE = M,
BE ∩FD = N доказать, что МN ║ АВ.
Обозначим равные дуги АF и ВС – α, тогда , то около четырехугольника ARHQ можно описать окружность, приняв отрезок АН за диаметр. Построив ее, замечаем, что 0 , то точки В, Н, А1 и С1 лежат на одной окружности с диаметром ВН. Следовательно, 0 , что и требовалось доказать.
 |  |
б) Рисунок 9 иллюстрирует случай, когда в треугольнике АВС один угол (угол В) тупой. Рассуждение является точно таким же. Только точки В1 и Н как бы меняются местами. В этом случае точка пересечения высот оказывается расположенной вне треугольника.
Для прямоугольного треугольника точкой пересечения высот является вершина прямого угла.
Таким образом, рассмотренные задачи помогают понять суть метода вспомогательной окружности, использование которого помогает решать геометрические задачи.
- И.Ф.Шарыгин. Геометрия Дрофа М.: 2007.
- И.Ф.Шарыгин. Решение задач. Просвещение. М.: 2007.
🎦 Видео
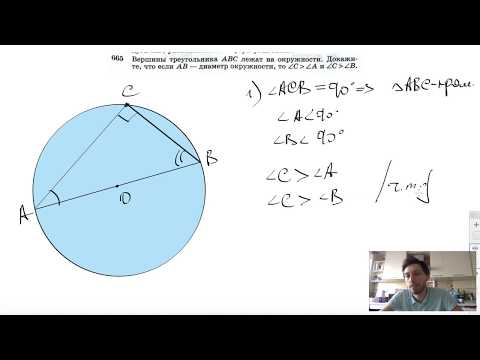
№665. Вершины треугольника ABC лежат на окружности. Докажите, что если АВ — диаметр окружностиСкачать
Доказать, что точки лежат в одной плоскости - bezbotvyСкачать

Окружность. 7 класс.Скачать

№8. Верно ли утверждение: а) если две точки окружности лежат в плоскостиСкачать

Доказать, что точки лежат на одной окружности Д301Скачать

26 Окружность девяти точекСкачать

Бондарев А.А. - 5. Доклад "О некоторых классах обеспечения неустойчивости"Скачать

10 класс, 11 урок, Числовая окружностьСкачать

Как искать точки на тригонометрической окружности.Скачать

#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

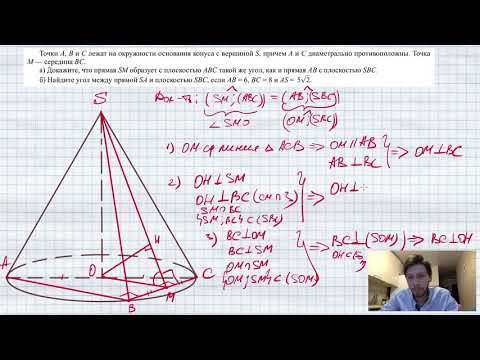
Точки A, B и C лежат на окружности основания конуса с вершиной S, причем A и C диаметрально противопСкачать
✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать

Определение принадлежности точки окружностиСкачать

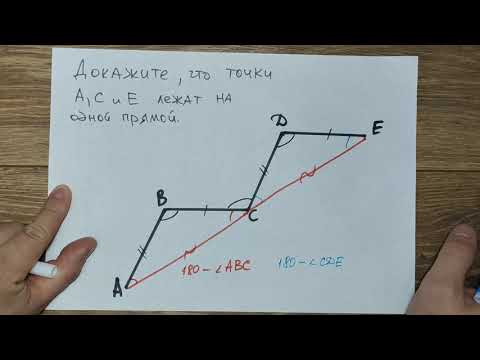
Задачка из советского учебника. Докажите, что точки А, С и Е лежат на одной прямойСкачать
Найти часть медианы треугольника, если некоторые его точки лежат на окружностиСкачать

Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

ЕГЭ Задание 16 Докажите, что три точки лежат на одной прямойСкачать