Изогональное сопряжение и педальные треугольники

Раиса Судиенко 3 лет назад Просмотров:

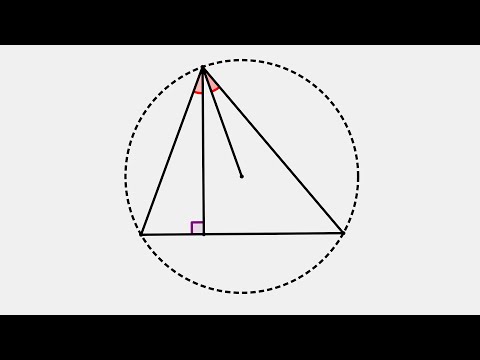
1 МАТЕМАТИЧЕСКИЙ КРУЖОК Изогональное сопряжение и педальные треугольники Д.ПРОКОПЕНКО ВПЕРВОЙ ЧАСТИ ЭТОЙ СТАТЬИ МЫ ПОвторим некоторые понятия и факты, связанные с изогональным сопряжением. Большинство из этих фактов известны и содержатся во многих источниках (см., например, недавнюю статью [1], для более глубокого изучения изогонального сопряжения рекомендуем статью [5]). Во второй части мы сконцентрируем свое внимание на замечательном факте о том, что изогонально сопряженные точки имеют общую педальную окружность. Оказывается, этот факт можно связать с сюжетами многих олимпиадных задач. Основные свойства изогоналей и геометрия треугольника Изогоналями относительно сторон угла (или изогональными прямыми) называются прямые, проходящие через вершину угла и симметричные относительно биссектрисы этого угла (рис.1). Часто используется следующее свойство изогоналей. Рис. 1 Свойство 1. Пусть AP и AQ изогонали угла с вершиной A, а B 1 и C 1 проекции Рис. 2 точки P на стороны угла (рис.2). Тогда AQ B C. 1 1 Упражнение 1. Докажите это свойство. Пусть из точки P на прямые BC, AC и AB опущены перпендикуляры PA 1, PB 1 и PC1 (рис. 3). Треугольник ABC называется Рис. 3 педальным треугольником точки P относительно треугольника ABC, а его описанная окружность педальной окружностью точки P. Если точка P лежит на описанной окружности треугольника АВС, то педальный треугольник вырождается и точки A 1, B 1, C 1 лежат на одной прямой. Будем использовать обозначения: O центр описанной окружности, H точка пересечения высот (ортоцентр) треугольника ABC. В следующем утверждении мы встречаем важный пример изогоналей в треугольнике: Радиус описанной окружности и высота, проведенные из одной вершины треугольника, изогональны относительно угла треугольника (рис.4). Упражнение 2. Докажите это.

2 МАТЕМАТИЧЕСКИЙ КРУЖОК 39 Рис. 4 Пусть в треугольнике ABC провели высоты. Треугольник с вершинами в основаниях высот называется ортотреугольником. Ортотреугольник является педальным треугольником ортоцентра H. Тогда по свойству 1 получаем: Радиус описанной окружности, проведенный из вершины треугольника, перпендикулярен соответствующей стороне ортотреугольника (рис.5). Рис. 6 Тогда AQ является серединным перпендикуляром к отрезку XY. Доказательство. Согласно свойству 1, AQ B1C 1, BC 1 1 XY (как средняя линия). Тогда AQ XY. Теперь заметим, что в точке A пересекаются серединные перпендикуляры к сторонам PX и PY треугольника PXY. Или чуть иначе: YA = AP = AX, тогда треугольник AXY равнобедренный, и перпендикуляр к стороне XY является серединным перпендикуляром к XY. Пусть точки X, Y и Z симметричны P относительно прямых AC, AB и BC (рис.7). Треугольник XYZ будем называть удвоенным педальным треугольником точки P относительно треугольника ABC. Из свойства 2 вытекает такое следствие: Изогонали являются серединными перпендикулярами к сторонам удвоенного педального треугольника. Рис. 5 Упражнение 3. Из точки K внутри треугольника ABC опущены перпендикуляры KA 1, KB 1 и KC 1 на стороны BC, AC, AB соответственно. Через точку A 1 проведена прямая l 1, параллельная прямой, симметричной прямой AK относительно биссектрисы угла A. Прямые l 2, l 3 определяются аналогично. Докажите, что прямые l 1, l 2, l 3 пересекаются в одной точке. Указание. Пусть прямые l A и AK изогонали BAC, тогда по условию l 1 l A. По свойству 1 имеем l BC 1 1. A Отметим еще одно свойство изогоналей. Свойство 2. Пусть AP и AQ изогонали относительно угла, а точки X и Y симметричны P относительно сторон угла (рис.6). Рис. 7

3 40 КВАНT $ 2017/ 9 Изогональное сопряжение Теорема 1. Пусть точка P не лежит на описанной окружности треугольника ABC. Тогда прямые, изогональные к прямым AP, BP и CP, пересекаются в одной точке (рис.8,а). Рис. 8 Обозначим точку пересечения Q. Точка Q называется изогонально сопряженной для точки P. Можно также говорить, что точки P и Q изогонально сопряжены. Пользуясь следствием из свойства 2, мы можем доказать теорему и сразу получить геометрический смысл точки Q: это центр описанной окружности удвоенного педального треугольника XYZ. Теорему 1 используют и в немного другой формулировке. Теорема 1. Если AP и AQ, BP и BQ две пары изогоналей в треугольнике ABC, то CP и CQ тоже изогонали (рис.8,б). Отметим, что если точка P лежит на описанной окружности и отлична от вершин треугольника ABC, то изогонали к AP, BP и CP параллельны друг другу. Упражнение 4. Докажите это. Очевидно, биссектриса изогональна сама себе. Тогда центр вписанной и центры вневписанных окружностей изогонально сопряжены сами себе. Упражнение 5. а) На биссектрисе угла A треугольника ABC внутри треугольника взяты точки D и F так, что DBC FBA. Докажите, что DCB FCA. б) Точка M расположена внутри треугольника ABC, A 1 точка, симметричная M относительно внешней биссектрисы угла A; аналогично определяются точки B 1, C 1. Докажите, что прямые AA, BB 1 и CC 1 пересекаются в одной точке. 1 в) Пусть AA 0, BB 0, CC 0 высоты в треугольнике ABC, M произвольная точка, A 1 точка, симметричная M относительно стороны BC; аналогично определяются точки B 1, C 1. Докажите, что прямые BB, 0 1 CC 0 1, AA 0 1 пересекаются в одной точке. Указания. б) Прямые пересекаются в точке, изогонально сопряженной M относительно треугольника ABC; в) докажите, что стороны треугольника ABC лежат на внешних биссектрисах для треугольника ABC 0 0 0, и воспользуйтесь п.б). Центр описанной окружности и ортоцентр Вспомним, что радиус описанной окружности и высота, проведенные из одной вершины треугольника, изогональны. Тогда точки O и H изогонально сопряжены. Упражнение 6. а) Пусть прямая a проходит через вершину A треугольника ABC и перпендикулярна стороне BC 1 1 ортотреугольника. Прямые b и c определяются аналогично. Докажите, что прямые a, b и c пересекаются в одной точке. б) Пусть H1, H2, H 3 точки, симметричные H относительно сторон треугольника ABC. Докажите, что точки H1, H2, H 3 лежат на описанной окружности треугольника ABC. в) Через основание высоты AA 1 треугольника ABC проведена прямая l 1, параллельная прямой AO. Прямые l 2, l 3 определяются аналогично. Докажите, что прямые l 1, l 2, l 3 пересекаются в одной точке. Точка пересечения касательных и удвоенная медиана Пусть AM медиана треугольника ABC. Сделаем стандартное построение. Удвоим медиану AM за точку M и получим точку D. Построим точку P, изогональную к D. Для этого достаточно построить изогонали к BD и CD. Пусть углы треугольника равны A, B, C. Отложим от стороны BA угла ABC изогональ к BD (рис. 9,а). Тогда эта прямая образует со стороной BC угол. Аналогично построим изогональ к CD. Пусть полученные прямые пересекаются в точке P. Мы получили, что PBC PCB BAC. По известному признаку (угол между касательной и хордой) PB и CP касательные к описанной окружности треугольника ABC. Тогда по теореме 1 AP является изогональю для медианы AM относительно угла BAC. Эта изогональ называется симедианой. Мы получили основное свойство симедианы:

4 МАТЕМАТИЧЕСКИЙ КРУЖОК 41 Рис. 9 Cимедиана, проведенная через вершину A, проходит через точку пересечения касательных, проведенных в точках B и C к описанной окружности треугольника ABC (рис. 9,б). Подробнее о свойствах симедианы можно прочитать в статье [4]. Упражнение 7. а) (Устная олимпиада по геометрии, 2004 г.) Пусть C 1 и B 1 проекции точки P пересечения касательных, проведенных в точках B и C к описанной окружности треугольника ABC, AM медиана. Тогда AM B1C 1. б) (Всероссийская олимпиада, 2013 г.) Остроугольный треугольник ABC вписан в окружность. Касательные, проведенные к в точках B и C, пересекаются в точке P. Точки D и E основания перпендикуляров, опущенных из точки P на прямые AB и AC. Докажите, что точка пересечения высот треугольника ADE является серединой отрезка BC. Общая педальная окружность Вернемся к изучению свойств изогоналей угла. Пусть AP и AQ изогонали угла BAC. Свойство 3. Проекции точек P и Q на стороны угла AB и AC лежат на одной окружности (рис.10), причем центр этой окружности середина отрезка PQ. Упражнение 8. Докажите это свойство. Теперь мы готовы доказать основную теорему этого раздела. Теорема 2. Педальные окружности изогонально сопряженных точек P и Q совпадают. Доказательство. По свойству 3 проекции точек P и Q на прямые AB и BC лежат на одной окружности (рис.11). То же верно и для проекций точек P и Q на прямые AB и AC. Но эти две окружности имеют общий Рис. 11 Рис. 10 центр середину отрезка PQ. Кроме того, они имеют общую точку, значит, эти окружности совпадают. Упражнение 9 (финальный тур Олимпиады имени И.Ф.Шарыгина, 2006 г.). Дан треугольник ABC и точка P внутри него. Точки A, B, C проекции P на прямые BC, CA, AB. Докажите, что центр окружности, описанной около треугольника ABC, лежит внутри треугольника ABC. Посмотрим, какой результат даст теорема 2 для уже знакомой пары изогонально сопряженных точек O и H. Вершины педального треугольника точки O середины сторон, а для точки H основания высот. Тогда по теореме 2 все эти шесть точек лежат на

5 42 одной окружности. Эта окружность называется окружностью Эйлера. Далее применим нашу теорию для решения задач. Четырехугольник с двумя равными противоположными углами Задача 1. Диагонали параллелограмма ABCD (отличного от прямоугольника) пересекаются в точке M (рис.12). Докажите, что точка M, а также основания КВАНT $ 2017/ 9 перпендикуляров, опущенных из точки D на прямые BC, CA и AB, лежат на одной окружности. Переформулируем задачу. Надо доказать, что точка M лежит на педальной окружности точки D относительно треугольника ABC ( ABC педальный треугольник точки D). По теореме 2 на этой же окружности лежат проекции на стороны треугольника ABC изогонально сопряженной точки. Если мы докажем, что одна из проекций совпала с M, то задача решена. Решение. Построим точку P, изогонально сопряженную к D. Поскольку BD удвоенная медиана, то, по свойству симедианы, P точка пересечения касательных к описанной окружности треугольника ABC, проведенных в точках A и C (рис.13). По теореме 2 точки P и D имеют общую педальную окружность. Точка M проекция точки P на AC. Следовательно, точка M лежит на окружности ABC Оказывается, что эту задачу можно обобщить. Задача 2 (о четырехугольнике). В выпуклом четырехугольнике ABCD углы A и С равны (рис.14). Докажите, что основания Рис. 12 Рис. 14 перпендикуляров, опущенных из точки D на прямые AB, BC, AC, и середина отрезка AC лежат на одной окружности или на одной прямой. Упражнения 10. Докажите это. Указание. Пусть точка P изогонально сопряженная к D относительно треугольника ABC. Докажите, что M проекция P на AC. 11 (М991). В треугольнике ABC точка M середина BC, H основание высоты, проведенной из A на BC. Точки P и Q внутри угла BAC выбраны так, что BAP CAQ, BP PA, AQ QC (рис.15). Докажите, что точки P, Q, M и H лежат на одной окружности. Рис. 13 Рис. 15

6 Указание. Эта конструкция похожа на задачу о четырехугольнике. 12 (Московская математическая олимпиада, 1987 г.). Точка P внутри треугольника ABC такова, что PBA PCA (рис.16). Пусть C 1 и B проекции точки P на стороны AB и AC 1 МАТЕМАТИЧЕСКИЙ КРУЖОК 43 Рис. 17 Рис. 16 соответственно, M середина BC. Докажите, что MB1 MC1. Указание. Заметим, что в условии уже есть проекции точки P на две стороны и середина стороны. Добавим еще точку A 1 проекцию точки P на сторону BC. Таким образом можно построить конструкцию из задачи 2 (для случая невыпуклого четырехугольника ABPC). Останется доказать равенство хорд в окружности, проходящей через A 1, B 1, C 1, M. Снова точка пересечения касательных и удвоенная медиана Рассмотрим точку Р пересечения касательных к описанной окружности треугольника ABC, проведенных в точках B и C, и удвоенную медиану AD (рис.17). Воспользуемся теперь теоремой об общей педальной окружности, чтобы «придумать» задачу. Мы уже знаем, что точки P и D изогонально сопряжены и у них общая педальная окружность. А теперь «спрячем» некоторые элементы конструкции. Именно, попробуем избавиться в условии задачи от точки D (которая была бы подсказкой к решению). Проведем высоту AH. Поскольку ABDC параллелограмм, то проекция X точки D на BC и точка H симметричны относительно середины M отрезка BC, т.е. CX = BH. Теперь мы готовы сформулировать задачу, которая практически эквивалентна сложной олимпиадной задаче (упражнение 13). Задача 3. В остроугольном неравнобедренном треугольнике ABC проведена высота AH, точка M середина BC. Касательные к описанной окружности треугольника ABC, проведенные в точках B и C, пересекаются в точке P. На стороне BC отложили отрезок CX = BH. Точки E и F проекции точки P на стороны AB и AC. Докажите, что точки E, F, M и X лежат на одной окружности. Упражнения 13 (Всероссийская олимпиада, 2015 г.). В остроугольном неравнобедренном треугольнике ABC проведены медиана AM и высота AH. На прямых AB и AC отмечены точки Q и P соответственно так, что QM AC и PM AB (рис.18). Окружность, описанная около треугольника PMQ, пересекает прямую BC вторично в точке X. Докажите, что BH = CX. Рис. 18

7 44 КВАНT $ 2017/ 9 Рис. 19 Указание. «Верните» на чертеж точку пересечения касательных к описанной окружности треугольника ABC в точках B и C и воспользуйтесь результатом упражнения 7,б. 14 (заочный тур Олимпиады имени И.Ф.Шарыгина, 2017 г.). Касательные к описанной окружности треугольника ABC, проведенные в точках A и B, пересекаются в точке D. Окружность, проходящая через проекции D на прямые BC, CA, AB, повторно пересекает AB в точке C. Аналогично строятся точки A, B. Докажите, что прямые AA, BB, CC пересекаются в одной точке. В завершение попробуем решить еще одну довольно сложную задачу. Задача 4 (Иранская олимпиады по геометрии, 2014 г.). Пусть H основание высоты из вершины A треугольника ABC и H точка, симметричная точке H относительно середины стороны BC (рис. 19,а). Касательные к описанной окружности треугольника ABC, проведеные в точках B и C, пересекаются в точке X. Перпендикуляр к XH, проведенный в точке H, пересекает прямые AB и AC в точках Y и Z соответственно. Докажите, что YXB ZXC. Решение. Рассмотрим случай остроугольного треугольника (другие случаи читатель может разобрать аналогично). Поскольку BX и CX касательные, имеем CBX BCX A, откуда BXC A. Пусть XYZ, XZY. Для решения достаточно доказать, что YXZ 2 A или, эквивалентно, 2 A. Пусть E и F проекции точки X на AB и AC (рис.19,б). Заметим, что четырехугольник XH YE вписанный, следовательно, XYH XEH. Аналогично, XZH XFH. Из четырехугольника AEXF найдем EXF 180 A. Остается убедиться, что EH F 180 A (тогда по сумме углов в четырехугольнике XFH E получим, что 2 A ). Пришла пора применить полученные знания про эту конструкцию. Нам уже известно, что точки E, M (середина BC), H, F лежат на одной окружности. Тогда EH F EMF. Кроме того, согласно упражнению 7,б, EM AC, FM AB, откуда легко получаем, что EMF 180 A. Задача решена. Список литературы 1. П.Кожевников. Изогонально сопряженные точки. «Квант», 2016, В.В.Прасолов. Точки Брокара и изогональное сопряжение. М.: МЦНМО, А.В.Акопян. Геометрия в картинках. М.: МЦНМО, Ю.Блинков. Симедиана. «Квант», 2015, А.Акопян, А.Заславский. Разные взгляды на изогональное сопряжение. «Математическое просвещение», 2007, вып. 11.

Видео:Геометрическое решение задачи из видео Бориса Трушина. Изогональное сопряжение.Педальный треугольникСкачать

Теорема Ван Ламуна

В этой работе рассмотренна недавно открытая теорема Ван Ламуна. Объектом исследования являются свойства медиан.

Актуальность работы обосновывается тем, что данная теорема была открыта за относительно недавний срок — всего лишь 10 лет.

Целью работы является исследование различных фактов связанных с медианами и впоследствии доказательство выше озвученной теоремы.

Видео:Богдан Бутырин, "Изогональное сопряжение и педальные треугольники"Скачать

Скачать:

Видео:Изогональное сопряжение | Олимпиадная математикаСкачать

Предварительный просмотр:

ГЛАВА 1 Вступление. Формулировка теоремы Ван Ламуна. 3

1.1Медиана. Точка пересечения медиан. 4

ГЛАВА 2 Теоремы связанные с медианами. 5

2.1 Понятие изогонального сопряжения. Точка Лемуана. 6

2.3Замечательные линии, связанные с центроидом. 8

ГЛАВА 3 Практическая часть. Доказательство Теоремы Ван Ламуна. 13

Список используемых источников и литературы. 20

В моей работе я бы хотел рассмотреть совсем недавно открытую теорему-теорему Ван Ламуна.

Объектом моего исследованияявляются свойства медиан.

Актуальность моей работы обосновывается тем, что данная теорема была открыта за относительно недавний срок — всего лишь 10 лет.

Целью моей работы является исследование различных фактов связанных с медианами и впоследствии доказательство выше озвученной теоремы.

С данной теоремой меня познакомил мой учитель математики, и она сразу поразила меня своим классическим характером. Замечу, что данная теорема широко не известна и моя работа призвана восполнить данный пробел.

Теорема Ван Ламуна может быть доказана школьными методами.

Методы исследования, которые использовались в данной работе:

1. Изучение всех свойств, необходимых для доказательства данной теоремы
2. Изучение литературы связанной с данной проблемой
3. Практическая работа -непосредственное доказательство данной теоремы

Формулировка теоремы Ван Ламуна.

Геометрия существует уже 3 тысячелетия, а треугольник основополагающая фигура геометрии. Казалось бы, что нового может быть нового в изученной вдоль и поперёк такой области геометрии, как треугольник?

Но в 1913 году Фрэнком Морли была открыта удивительная теорема, которая утверждает:

Точки пересечения смежных трисектрис углов произвольного треугольника являются вершинами равностороннего треугольника.

Рис.1(Теорема Морлея) Рис.2(Теорема Ван Ламуна)

На рисунке 1 три разноцветных угла при каждой вершине большого треугольника равны. Теорема утверждает, что независимо от выбора большого треугольника маленький фиолетовый треугольник будет равносторонним.

Разумеется, подобные, носящие классический характер теоремы рождаются нечасто. Ведь уже сейчас крайне затруднительно обнаружить утверждение, формулируемое в основных геометрических понятиях, нетривиально доказуемое и при этом никому не известное, учитывая почтенный возраст геометрии как науки.

Что может быть красивее этой теоремы? Но вот в 2002 году геометр из Голландии Фло Ван Ламун открыл удивительную теорему, сравнимую по эстетическим параметрам с теоремой Морлея:

Центры описанных окружностей, описанных около шести треугольников на которые произвольный треугольник разбивается своими медианами лежат на одной окружности. (Рис.2)

Моей основной целью является доказательство этой красивой теоремы. Я также докажу справедливость обратного утверждения, а попутно вспомню другие интересные свойства точки пересечения медиан треугольника.

1.1 Медиана. Точка пересечения медиан.

Для начала вспомним, что же такое медиана?

Медиана треугольника — чевиана [1] , соединяющая вершину треугольника с серединой противоположной стороны, а также прямая, содержащая эту чевиану.

Основное свойство медианы:

Медианы треугольника пересекаются в одной точке, которая называется центроидом (центром тяжести) , и делятся этой точкой на две части в отношении 2:1, считая от вершины.

Из множества имеющихся доказательств этой теоремы приведём два.

Поместим в точки A, B и C единичные массы. Пусть O—центр масс этой системы точек(он существует по свойству центра масс). Точка O является также центром масс точки A с массой 1 и точки с массой 2, где A1—центр масс точек B и C с единичными массами, т. е. A1—середина отрезка BC. Поэтому O лежит на медиане AA1и делит её в отношении AO:OA1 = 2:1. Аналогично доказывается, что остальные медианы проходят через точку O и делятся ею в отношении 2:1.

Из данного доказательства следует физическое свойство центроида:

Точка пересечения медиан является центром тяжести треугольника.

Выберем произвольную точку O в качестве общего начала векторов. На медиане AA1 возьмём точку G, делящую её в отношении 2:1(рис.3), считая от точки A. Тогда на основании формулы деления отрезка в данном отношении будем иметь:OA 1 = (OB+OC);OG=,

Рис.3 (Векторное доказательство свойства медиан)

Из этих равенств следует OG =1/3(OA + OB + OC).

Так как в данное выражение векторы OA, OB и OC вершин треугольника ABC входят симметрично. Поэтому векторы точек, которые делят другие две медианы в отношении 2:1, будут иметь то же самое выражение. Это и означает, что делящие точки совпадают.

Из данного выражения вытекает важнейшее характеристическое свойство центроида: Точка O совпадает с центроидом G треугольника ABC

тогда и только тогда, когда верно векторное равенство:

Доказав существования точки пересечения медиан обратимся к её свойствам и свойствам самой медианы.

1.Имеются всего 4 точки P в плоскости треугольника ABC такие, что треугольники BCP,CPA,APB равновелики. Внутри треугольника это его центроид, а вне вершины его антикомплиментарного [2] треугольника.

2.Медианы треугольника разбивают треугольник на 6 равновеликих треугольников(треугольников с равными площадями).

3.Из медиан треугольника можно составить треугольник,т.к. три вектора, дающие нулевой по свойству можно представить в виде замкнутой ломаной.

Теоремы, связанные с медианами.

Рассмотрев основные свойства медиан, перейдём к теоремам, каждая из которых легко доказываются через полученные свойства.

Теорема №1(Теорема Лагранжа-Лейбница)

Для любой точки P выполняется векторное равенство РА 2 +РВ 2 +РС 2 =GA 2 +GB 2 +GC 2 +3PG 2

Так как скалярный квадрат вектора есть просто квадрат его длины, то:

(PG+GA;PG+GA)+(PG+GB;PG+GB)+(PG+GC;PG+GC)=GA 2 +GB 2 +GC 2 +3PG 2 +2(PG;GA+GB+GC),в силу свойства (1) последнее слагаемое равно 0 =>ч.т.д.

Из данной теоремы следует ряд важных следствий

1. a 2 =4/9(2m 2 b +2m 2 c -2m 2 a ),если принять в роли P сторону BC.
2. 2.m 2 a =1/4(2b 2 +2c 2 -a 2 )-длина медианы через стороны треугольника.

1. m 2 a + m 2 b + m 2 c =3/4(a 2 +b 2 +c 2 )

4)9OG 2 =9R 2 -(a 2 +b 2 +c 2 ).

Теорема Паппа. Пусть X,Y,Z и X’,Y’,Z’ коллинеарные(принадлежащие одной прямой) тройки точек. Прямые XY’ и X’Y пересекаются в точке А, прямые YZ’ и Y’Z – в точке В, прямые ZX’ и Z’X – в точке С. Тогда точки А,В,С коллинеарны.

Красиво, не правда ли? Заметим, что справедлива и обратная теорема Паппа.

Дадим определение изогональному сопряжению:

Изогональное сопряжение — геометрическое преобразование, при котором любой чевиане в треугольнике ставится в соответствие чевиана,симметричная ей относительно биссектрисы. На рис точки Pи P’ изогонально сопряжены относительно биссектрисы угла А.

Существует несколько пар изогонально сопряжённых точек. Выделим главные:

1.Ортоцентр и центр описанной окружности.

2.Точка Торричелли точка Аполллония.

3.Центроид и точка Лемуана.

Так как моя научная работа связана с центроидом, то здесь я рассмотрю только третий пункт.

Прямая изогонально сопряжённая медиане называется симедианой и соответственно:

Точка Лемуана [3] -точка пересечения симедиан.

С точкой Лемуана связано несколько замечательных свойств:

1. Сумма квадратов расстояний от точки на плоскости до сторон треугольника минимальна, когда эта точка является точкой Лемуана.
2. Расстояния от точки Лемуана до сторон треугольника пропорциональны длинам сторон.
3. Если провести через точку Лемуана отрезки, параллельные сторонам треугольника, с концами на сторонах, то концы этих отрезков будут лежать на одной окружности(рис.8).

Введём ещё одно новое определение:

Опустим из некоторой точки Р перпендикуляры на прямые, проходящие через стороны треугольника АВС и отметим основания этих перпендикуляров. Они являются вершинами треугольника, который называется педальным треугольником точки Р.(рис.9).

Треугольник A1B1C1 является педальным треугольником точки P.

Кстати, окружность, описанная около педального треугольника, называется педальной окружностью.

Из определения педального треугольника появляется ещё одно свойство точки Лемуана, которое нам понадобится в дальнейшем.

4.Точка Лемуана К является центроидом своего педального треугольника. Заметим, что педальный треугольник вырождается в отрезок в том и только том случае, когда Pлежит на описанной окружности треугольника. Прямая LMN является прямой Симсона [4] (рис.10).

2.3 Замечательные линии и центроид

С центроидом связано множество замечательных линий. В данной работе рассмотрим некоторые из них.

В любо неравностороннем треугольнике его ортоцентр Н, центроид G и центр описанной окружности O лежат на одной прямой(рис.11).

Мы сразу докажем этот красивый факт, если рассмотрим гомотетию [5] с центром в точке пересечения медиан G и коэффициентом .

Действительно, так как медианы делятся центроидом G в отношении 2:1, считая от вершин, указанная гомотетия переводит треугольник АВС в его серединный треугольник . Кроме того, очевидно, что центр О описанной около треугольника АВС окружности совпадает с ортоцентром серединного треугольника. Но гомотетия, являясь преобразования подобия, переводит соответствующие элементы треугольника в соответствующие — в частности, ортоцентр переходит в ортоцентр: . [6]

2.Существует ещё одна замечательная прямая схожая с предыдущей –прямая Нагеля(рис.12).

Прежде чем сформулировать соответствующую теорему (доказательство которой будет полностью аналогично предыдущему, но потребует несколько больших усилий), необходимо только напомнить, что такое точка Нагеля.

Прямые, соединяющие вершины треугольника с точками касания соответствующих вневписанных окружностей с его сторонами, называют точкой Нагеля N.

То, что эта точка действительно существует, несложно показать с помощью теоремы Чевы.

В любом треугольнике его точка Нагеля N, центроид G, и центр вписанной окружности I лежат на одной прямой, причём(точка G лежит внутри отрезка NI),которая называется прямой Нагеля.

Достаточно убедиться в том, что гомотетия с центром в точке пересечения медиан и коэффициентом переводит точку Нагеля в центр вписанной окружности.

Иначе говоря, достаточно показать, что прямая, соединяющая вершину А треугольника с соответствующей точкой касания вневписанной окружности перейдёт при этой гомотетии в прямую, проходящую через центр вписанной окружности I (потому что дальше мы точно также сумеем показать, что и образы двух других чевиан, проходящих через точку Нагеля, будут проходить через центр вписанной окружности, а точка пересечения прямых должна переходить в точку пересечения их образов).

Стало быть, образ нашей прямой есть некоторая прямая, проходящая через середину стороны ВС – точку (поскольку рассматриваемая гомотетия вершину треугольника переводит в середину противолежащей стороны), причём параллельно исходной прямой (образ прямой, не проходящей через центр гомотетии есть параллельная ей прямая).

Замечу ещё, что прямая, соединяющая вершину треугольника А с точкой касания вневписанной окружности со стороной ВС, проходит через точку , диаметрально противоположную точке касания вписанной окружности со стороной ВС (т.е. симметричную ей относительно центра вписанной окружности) – что сразу следует из рассмотрения гомотетии с центром в А, переводящей вписанную окружность во вневписанную: точка переходит в точку.

Отсюда я заключаю, что образ прямой есть средняя линия в треугольнике (точки касания вписанной и описанной окружности со стороной ВС симметричны относительно её середины), и потому проходит через центр вписанной окружности.

3.Добавочные точки и прямые Нагеля

Обратим теперь внимание на то, что центр вписанной окружности I имеет три родственные ей точки — центры окружностей вневписанных, обладающих схожими свойствами. [7]

Рис.14 (Добавочная точка Нагеля)

Оказывается, слабой является и точка Нагеля.

Пусть– точка касания вписанной окружности со стороной ВС, – точка касания вневписанной окружности с центром вс продолжением стороны ВА, а – точка касания вневписанной окружности с центром в с продолжением стороны СА. Тогда прямыепересекаются в одной точке. Её называют первой добавочной точкой Нагеля и обозначают N a . Две другие добавочные точки определяются аналогично.

Поскольку слабые точки ходят «четвёрками», любая теорема, в формулировке которой они фигурируют, имеет трёх «сестёр».

Есть три сестры и у прямой Нагеля.

Отрезок с концами в добавочной точке Нагеля и соответствующей ей центре вневписанной окружности, содержит центроид G и делится им в отношении 2:1.

После рассмотрения прямых перейдём к одной замечательной окружности.

Окружность Эйлера (окружность девяти точек,окружность Фейербаха(доказал существование данной окружности),окружность шести точек) — получила такое название из-за следующей теоремы:

Основания трёх высот произвольного треугольника, середины трёх его сторон и середины трёх отрезков, соединяющих его вершины с ортоцентром, лежат все на одной окружности. [8]

Свойства окружности 9 точек:

1. Центр окружности девяти точек лежит на прямой Эйлера , точно в середине отрезка между ортоцентром и центром описанной окружности.
2. Радиус окружности девяти точек равен половине радиуса описанной окружности. Более того, описанная окружность есть образ окружности девяти точек относительно гомотетии
3. Окружность девяти точек произвольного треугольника касается вписанной и всех трёх вневписанных окружностей этого треугольника. [9]

Доказательство теоремы Ван Ламуна

Перейдём непосредственно к доказательству основной теоремы.

Рассмотрим произвольную точку Р, лежащую в плоскости треугольника АВС. Чевианы, проходящие через данную точку разобьют исходный треугольник на 6.

Отметим в каждом из них центр описанной окружности так, как показано на рисунке. Таким образом получаем шестиугольник A + С – В + А — С + В — (рис.17)

Наша цель доказать следующую теорему:

Вершины шестиугольника лежат на одной окружности тогда и только тогда, когда или Р является центроидом треугольника(окружность Ламуна) или Р является ортоцентром треугольника (окружность Эйлера).

Существуют 2 случая:

1)Случай шести, пяти различных вершин.

2)Случай нескольких совпадений.

Попытаемся разобрать первый случай.

Случай шести или пяти различных вершин.

Пусть все 6 вершин различны или же совпадает одна пара(как будет видно из наших дальнейших рассуждений случай для 6 вершин подходит к случаю, когда пара вершин совпадает).

Видео:Снова стереома + изогональное сопряжение | Готовимся ко ВсероссуСкачать

Понятно, что в нашем случае (центры окружностей лежат на серединных перпендикулярах) мы шестиугольник специального вида противоположные стороны, которого параллельны(A + С – параллельно А — С + ,так как оба этих отрезка перпендикулярны BB 1 и т.д.)

Видео:ПЕДАЛЬНЫЙ треугольникСкачать

Шестиугольник такого вида будем называть шестиугольником-параллелограммом.

Видео:Почему геометрия — это красиво?Скачать

Отрезки A + A — ,B + B — ,C + C —

Видео:Олимпиады 2022. Антипараллельность. Симедиана. Повороты. Изогональное сопряжение. ГомотетияСкачать

Свойства шестиугольников-параллелограммов:

1. Вершины шестиугольника-параллелограмма расположены на коническом сечении. Между прочим, теперь становится ясно, что окружность, которая возникает при Р=G, явление, конечно, исключительное и особенное, но все же не слишком — окружность ведь представляет собой частный (вырожденный) случай конического сечения.

Доказательство сразу следует из обратной теоремы Паскаля.

Обратная теорема Паскаля: если точки пересечения противоположных сторон шестиугольника лежат на одной прямой (коллинеарны), то вершины шестиугольника расположены на некоторой конике(рис.18).

Видео:Педальный треугольникСкачать

Но в нашем шестиугольнике-параллелограмме противоположные стороны параллельны.

Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Рис.18

Видео:✓ Решаем с ходу странную задачу | #вызов | Борис ТрушинСкачать

2. Около шестиугольника-параллелограмма можно описать окружность тогда и только тогда, когда его главные диагонали равны(рис.19).

Видео:Три середины на одной прямой | Готовимся ко ВсероссуСкачать

Рис.19

Видео:СЕКРЕТНАЯ "Лемма 255" в №16 из ЕГЭ 2020 по профильной МАТЕМАТИКЕСкачать

Доказательство:

Пусть окружность описать можно. Тогда, например, трапеция В + В — С + С — , как вписанная в окружность, является равнобокой. Поэтому В + В — = С + С — Аналогично, в равнобокой трапеции С + С — А + А — равны диагонали, следовательно, С + С — = А + А — .

Обратно, если диагонали равны, то мы имеем три пары равнобоких трапеций. Отметим точки пересечения продолжений их боковых сторон – получим треугольник PQR. Серединные перпендикуляры к основаниям трапеций будут совпадать с соответствующими биссектрисами углов треугольника PQR, а значит, пересекутся в центре вписанной в этот треугольник окружности, т.е. найдётся точка, равноудалённая от всех вершин.

Обозначим ортогональные проекции векторов ,, на прямые АА 1 , ВВ 1 , СС 1 соответственно, как . (рис.20)

Тогда справедливы равенства:

Видео:Хардовая геома 10.7 | Готовимся ко ВсероссуСкачать

Рис.20

Видео:Олимпиадная задача для 14-15 лет, которая вынесла всехСкачать

Докажем следующее утверждение:

Центры окружностей (среди которых нет совпадающих), описанных около треугольников, на которые чевианы, проходящие через центроид G, разбивают исходный треугольник, лежат на одной окружности.

Рассмотрим треугольник, составленный из медиан, как из векторов, обозначив , , . (Рис.21)

Согласно Свойству 3, проекции вектора А + А — , отложенного от вершины A* этого треугольника, равны по длине половинам соответствующих сторон. И т.д. – отсюда получаем, что длины этих трёх векторов равны радиусу окружности, описанному около треугольника, составленного из медиан. Итак, главные диагонали шестиугольника – параллелограмма оказались равны, и в силу Свойства 2, около него можно описать окружность. Перейдём к рассмотрению следующей вспомогательной теоремы.

Если шесть различных центров окружностей, описанных около треугольников, на которые чевианы, проходящие через точку Р, разбивают исходный треугольник, лежат на одной окружности, то Р совпадает сего центроидом G.

Попробуем доказать, что в случае расположения центров на одной окружности,это и будет означать, что P=G.

Перепишем Утверждение 3 в терминах скалярного произведения векторов («произведение длин на косинус угла между ними»). Получится

утверждение 3 для скалярного произведения.

Отсюда, к примеру, следует, что , т.е. что эти два вектора ортогональны. Поскольку длины главных диагоналей равны ( Утверждение 2) , то ортогональными также будут и вектора В + В — +С + С — и В + В — -С + С — , так как их скалярное произведение равно 0. Отсюда, в свою очередь, вытекает коллинеарность векторов В + В — -С + С — и АА 1 , т.е. для некоторого числа k.

Совершенно аналогично находим, что и .

Сложив эти три равенства, как раз и получим, что .

Случай нескольких совпадений.

Осталось подробно разобрать случай, когда имеются совпадения центров описанных окружностей. Следующая лемма проясняет ситуацию.

Точки В + и С — совпадают тогда и только тогда, когда порождающая шестиугольник – параллелограмм точка Р лежит на окружности, симметричной описанной около исходного треугольника окружности относительно его стороны ВС.(рис.22)

Действительно, центры будут совпадать в том и только в том случае, когда точки АС 1 РВ 1 будут лежать на одной окружности. Пусть, для определённости, Р расположено «над» прямой ВС. Поскольку около четырёхугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов составляет развёрнутый, должно иметь место равенство , т.е. точка Р должна лежать на дуге окружности, и из этой точки отрезок ВС виден под углом . Этот же отрезок виден под таким же углом и из любой точки «нижней» дуги описанной около АВС окружности.

Случай в точности 4 центров невозможен, так как при этом возникает ещё одна совпадающая пара, и мы имеем ровно 3 различных центра, при том, что Р=Н. Все шесть треугольников, образованных чевианами, тогда получаются прямоугольными, и центры описанных окружностей будут находиться на серединах отрезков, соединяющих ортоцентр с вершинами. Конечно, тогда они лежат на одной окружности.

Итак, мы доказали:

Если чевианы проходят через ортоцентр Н, то центры описанных около 6 треугольников

(среди которых лишь три различных) окружностей, на которые чевианы разбивают данный треугольник, лежат на его окружности Эйлера.

И обратно, если мы имеем более 2 совпадающих центров, и все центры расположены на одной окружности — это означает, что на самом деле совпадающих центров ровно 3, точка Р. совпадает с ортоцентром Н, а общая окружность есть окружность Эйлера.

Основная Теорема теперь доказана полностью.

Стоит сказать ещё несколько слов о случае ровно 5 различных центров. Конечно, и здесь, как и в случае 6 центров, мы будем иметь окружность Ламуна. Но интересно отметить, что здесь мы имеем треугольник АВС совершенно специального вида – в этом треугольнике центроид должен лежать на окружности, симметричной описанной относительно одной из сторон треугольника

В данной работе мне удалось решить все проблемы, которые передо мной стояли. Подробно рассмотрев свойства и теоремы связанные с медианами, мне удалось выполнить и практическую часть – доказательство теоремы Ван Ламуна с помощью школьных методов.

Таким образом, я считаю, что моя работа является достаточно важной в области исследования свойств центроида.

Приложение. Список литературы и используемых интернет ресурсов.

1.Панарин Я.П. Элементарная геометрия Том 1/ Я.П.Панарин // Москва Издательство МЦНМО.-2004.-34-35стр.

2. A. Мякишев , «О некоторых окружностях, связанных с треугольником. Часть 1”/А.Мякишев//Математическое Образование № 3 (63).-2012.-10-37с;Математическое Образование № 2 (62).- 2012.-51,52с.

Видео:Изогонали угла. Радиус описанной окружности и высота, проведенные из одной вершины треугольника.Скачать

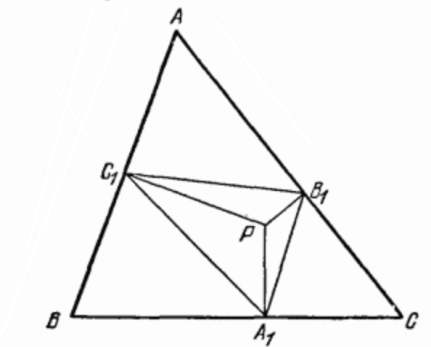
Проект «Педальный треугольник»

Проект по математике «Педальный треугольник» подготовила ученица 8 класса под моим руководством. Цель проекта: применение теорем о педальном треугольнике при решении задач. В работе дается определение педальному треугольнику, доказываются теоремы об этом треугольнике, также рассматриваются точка Брокара, треугольник и окружность Брокара. В практической части показывается как построить педальный треугольник, решаются задачи, в которых применяются теоремы о педальном треугольнике.

Просмотр содержимого документа
«Проект «Педальный треугольник»»

Департамент образования мэрии города Новосибирска

Дворец творчества детей и учащейся молодежи «Юниор»

Городской конкурс исследовательских проектов

учащихся 5-8 классов

Бобылева София Сергеевна

МБОУ ЭКЛ, 8 класс,

Центральный округ г.Новосибирска

Консультант проекта: Кривченкова

учитель математики ВК

Контактный телефон руководителя:

Основная часть 4

Что такое педальный треугольник? 4

Что такое точка Брокара? 4

Треугольник Брокара 5

Окружность Брокара 5

Теоремы о педальном треугольнике 6

Практическая часть 9

Список литературы 15

Искусство решать геометрические задачи

чем-то напоминает трюки иллюзионистов — иногда,

даже зная решение задачи, трудно

понять, как можно было до него додуматься.

Треугольник — первая геометрическая фигура, встречающаяся в древних орнаментах. В Египте он символизировал триаду духовной воли, любви, интуиции и высшего разума человека, то есть его личность или душу.

В герметической идеографии треугольник с устремленной к верху вершиной, символизирует огонь и отвечает идее вознесения, духовности.

Треугольник с горизонтальной чертой считается пассивным и означает воздух, умеренный огонь.

Перевернутый треугольник означает чашу, готовую принять воду; мудрость, порождающую главную идею.

Треугольник – одна из основных фигур, изучаемых в геометрии. В школьной программе рассматриваются несколько видов треугольников, а, чтобы расширить представление об этих необычайно интересных фигурах и их свойствах, мы захотели познакомиться с педальным треугольником. Свойства педального треугольника позволяют решать сложные математические задачи просто, красиво и понятно.

В нашей работе мы собираемся рассмотреть несколько вопросов этого раздела, исходя из этого, мы поставили перед собой следующие цель и задачи.

Цель: применение теорем о педальном треугольнике при решении задач.

Узнать, какой треугольник является педальным.

Изучить его историю.

Разобрать основные теоремы и свойства педального треугольника.

Решить несколько задач по данной теме.

Гипотеза: можно ли сказать, что применение теорем о педальном треугольнике помогает при решении сложных задач.

Методы исследования: сбор информации, обработка данных, сравнение, анализ, обобщение.

Первый этап – теоретический. Поиск и изучение теоретического материала (литературы и Интернет-ресурсов) по теме «Педальный треугольник».

Второй этап – практический. Доказательство теорем и свойств педального треугольника и решение задач с их использованием.

Третий этап – заключительный. Систематизация и обобщение теоретического материала. Анализ решения задач. Формулировка выводов.

Основная часть
Что такое педальный треугольник?

Пусть P любая точка внутри данного треугольника ABC и пусть перпендикуляры, опущенные из точки P на стороны BC, CA, AB треугольника будут P , P и P .

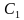
Определение: Треугольник 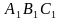, вершинами которого являются основания этих перпендикуляров, называется педальным (подерным) треугольником треугольника ABC для «педальной точки» P.

При торможении автомобиля педаль тормоза бьет обратно в педаль, работая по принципу – точка – тире — точка.

Что такое точка Брокара?

Точкой Брокара называется такая педальная точка, которая при соединении с вершинами треугольника образует равные чередующиеся углы. Такие углы называются углами Брокара.

Т очка Брокара — одна из двух точек внутри треугольника, возникающих на пересечении отрезков, соединяющих вершины треугольника с соответствующими свободными вершинами треугольников, подобных данному треугольнику и построенных на его сторонах.

Считаются замечательными точками треугольника, с их помощью строятся многие объекты геометрии треугольника (в том числе, окружность Брокара , треугольник Брокара , окружность Нейберга (см. также Нойберг, Жозеф), окружности Схоуте). Названы в честь французского метеоролога и геометра Анри Брокара, описавшего точки и их построение в 1875 году, однако были известны и ранее, в частности, были построены в одной из работ немецкого математика и архитектора Августа Крелле, изданной в 1816 году.

Брокар Анри (12.05.1845 – 16.02.1922) – французский математик, специалист в области геометрии треугольника и круга. Ряд геометрических образов, связанных с треугольником и кругом, носит в настоящее время имя Брокара (круг, первый и второй треугольники, точки и углы, но только «круг Брокара» принадлежит ему самому). Брокар составил один из наиболее подробных справочников по замечательным кривым. В работе имеются два плаката, формата А3, показывающие расположение точек Брокара внутри треугольника.

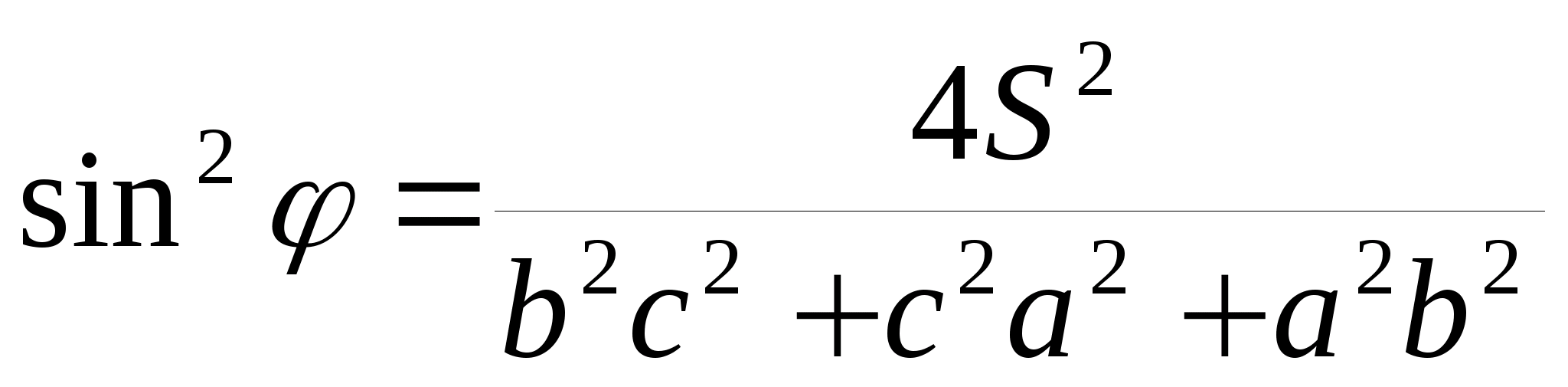
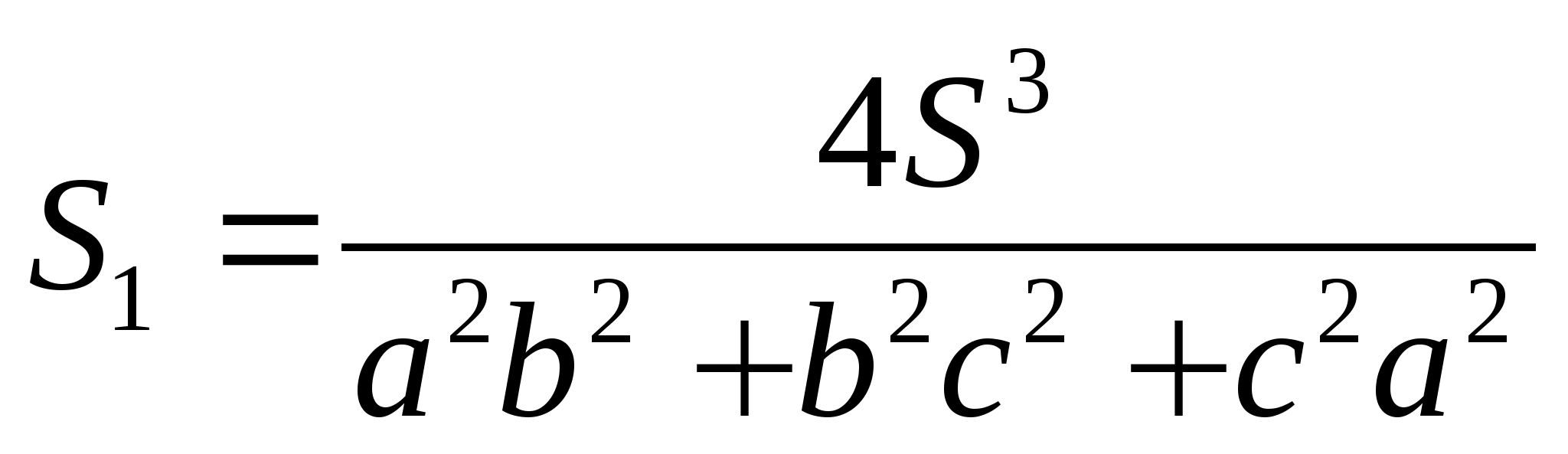
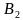
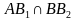
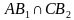
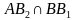
Угол Брокара определяется по формуле , а площадь педального треугольника точки Брокара равна , где S – площадь данного треугольника.

Треугольник Брокара – треугольник, образуемый точками пересечения линий, проведённых из двух различных вершин заданного треугольника через различные точки Брокара: для △ABC и его точек Брокара B1 и B2 вершины одного из треугольников Брокара будут находиться на пересечениях AB1∩BB2 , AB1∩CB2 и AB2∩BB1. Треугольник Брокара вписан в окружность Брокара.

Окружность Брокара (окружность семи точек) — окружность, диаметром которой является отрезок, соединяющий центр описанной окружности данного треугольника и его точку Лемуана. Две точки Брокара лежат на этой окружности, так же, как и три вершины треугольника Брокара. Эта окружность концентрическая с первой окружностью Лемуана.

В равностороннем треугольнике центр описанной окружности и точка Лемуана совпадают, поэтому его окружность Брокара вырождается в точку.

Теоремы о педальном треугольнике

Если точка Брокара Р является пересечением медианы СМ с биссектрисой АЕ, то треугольник правильный.

💥 Видео

Симедианы, точка Лемуана, изогональное и изотомическое сопряженияСкачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

✓ Расстояние от вершины треугольника до точки пересечения высот | Ботай со мной #113 | Борис ТрушинСкачать

ВСЕ свойства ортоцентра для №16 на ЕГЭ 2023 по математикеСкачать

Удивительный треугольник Паскаля | Лекции по математике – Яков Ерусалимский | Научпоп | НаукаPROСкачать