Из точки в окружности проведены касательная ва и секущая вд

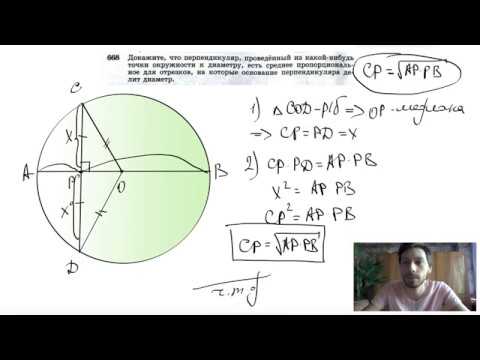
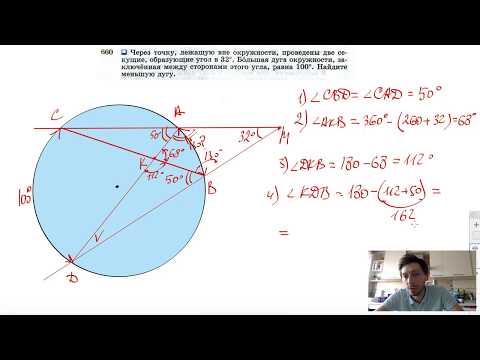
Вопрос по геометрии:

Из точки B к окружности проведены касательные BA и секущая BD. Найдите величину угла ABD, если дуги, высекаемые ими на окружностиб равны 209 и 97 градусовю Ответ дайте в градусах.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

дугаАД=209 дугаАс=97 . Угол АВС=(дугаАД-дугаАС)/2=(209-97)/2=56

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:№658. Через точку А к данной окружности проведены касательная АВ (В — точка касания) и секущая ADСкачать

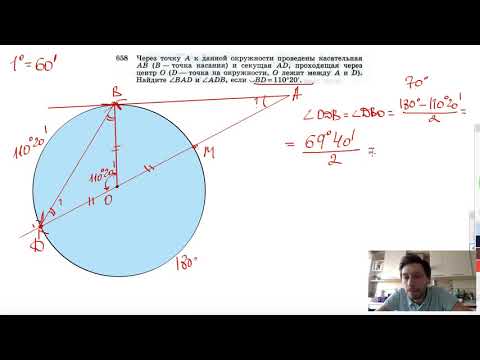
Из точки B к окружности проведены касательные BA и секущая BD?

Геометрия | 5 — 9 классы

Из точки B к окружности проведены касательные BA и секущая BD.

Найдите величину угла ABD, если дуги, высекаемые ими на окружностиб равны 209 и 97 градусовю Ответ дайте в градусах.

ДугаАД = 209 дугаАс = 97 .

Угол АВС = (дугаАД — дугаАС) / 2 = (209 — 97) / 2 = 56.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Касательные СА и СB к окружности образуют угол АСВ, равный 112гр?

Касательные СА и СB к окружности образуют угол АСВ, равный 112гр.

Найдите величину меньшей дуги АВ, стягиваемой точками касания.

Ответ дайте в градусах.

Видео:№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать

Касательная СА И СВ к окружности образует угол АСВ , равный 112 градусов?

Касательная СА И СВ к окружности образует угол АСВ , равный 112 градусов.

Найдите величину меньшей дуги АВ, стягиваемой точками касания.

Ответ дайте в градусах.

Видео:№670. Через точку А проведены касательные АВ (В — точка касания) и секущая, которая пересекаетСкачать

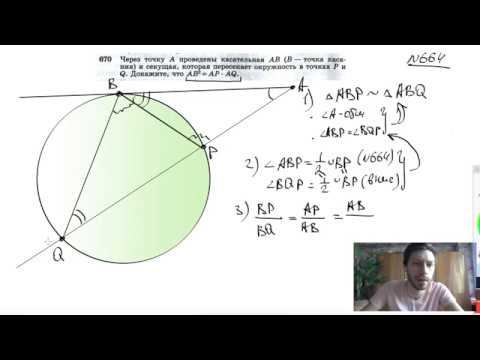
Через концы А, В дуги окружности в 56 градусов проведены касательные АС и ВС?

Через концы А, В дуги окружности в 56 градусов проведены касательные АС и ВС.

Найдите угол АСВ.

Ответ дайте в градусах.

Видео:Окружность, касательная, секущая и хорда | МатематикаСкачать

Прямая касаятся окружности в точке К?

Прямая касаятся окружности в точке К.

Точка О — центр окружности.

Хорда КМ образует с касательной угол.

Найдите величину угла ОМК.

Ответ дайте в градусах.

Видео:8 класс, 32 урок, Касательная к окружностиСкачать

Из одной точки к окружностм проведены две секущие?

Из одной точки к окружностм проведены две секущие.

Дуги, высекаемые секущими на окружности, равны 49 ° и 25 °.

Найдите угол между секущими, ответ выразительности в градусах.

Видео:№671. Через точку А проведены касательная АВ (В — точка касания) и секущая, которая пересекаетСкачать

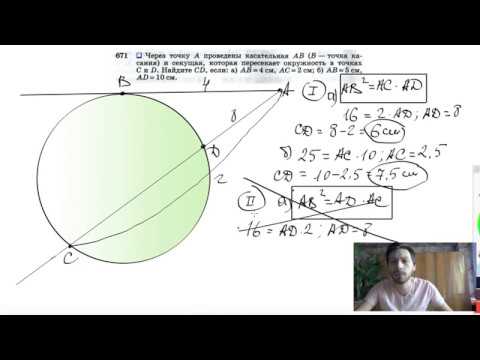
Касательная CA и CB к окружности образуют угол ACB, равный 130 градусам?

Касательная CA и CB к окружности образуют угол ACB, равный 130 градусам.

Найдите величину меньшей дуги AB, стягиваемой точками касания.

Ответ дайте в градусах.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Из точки K к окружности проведены касательные KM и KN?

Из точки K к окружности проведены касательные KM и KN.

Меньшая дуга MN равна 100 градусов.

Найдите угол MKN.

Ответ дайте в градусах.

Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Помогите с решение?

Помогите с решение.

Ответ должен быть 19 и 161 градус.

А вот как решить додуматься не могу.

Дуга окружности ВС равна 38(градусов).

Через точку А этой окружности проведены секущие АВ и АС найдите величину вписанного угла ВАС.

Видео:Профильный ЕГЭ 2023. Задача 16 планиметрия. С чего начать изучение?Скачать

Касательные CA и CB к окружности образуют угол АСВ, равный 90 градусов?

Касательные CA и CB к окружности образуют угол АСВ, равный 90 градусов.

Найдите величину меньшей дуги АВ, стягиваемой точками касания.

Ответ дайте в градусах.

Видео:№640. Даны окружность с центром О радиуса 4,5 см и точка А. Через точку А проведены две касательныеСкачать

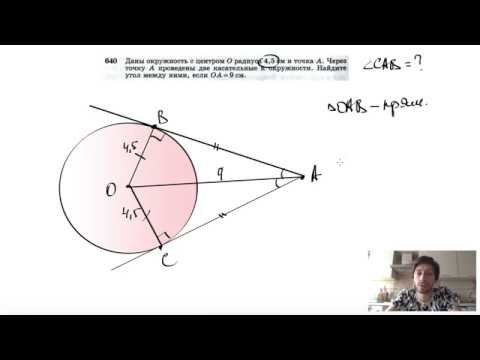
Прямая касается окружности в точке К?

Прямая касается окружности в точке К.

Точка О центр окружности.

Хорда КМ образует с касательной угол, равный 4 градуса.

Найдите величину угла ОМК.

Ответ дайте в градусах.

Вы находитесь на странице вопроса Из точки B к окружности проведены касательные BA и секущая BD? из категории Геометрия. Уровень сложности вопроса рассчитан на учащихся 5 — 9 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.

Данная величина есть площадь под графиком функции на отрезке [ — 1, 2], что по определению равно : Ответ : 12.

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник⇒ AB = BF = FE = EC Противоположные стороны равны. Пусть АВ = х, тогда : (х + 3х) * 2 = 88 4х = 88 / 2 4х = 44 х = 44 / 4 х = 11 см Ответ : АВ = 11 см.

Т. к. Против большего угла, лежит большая сторона, то первой будет сторона AC, второй по величине угол BCA (70°) следовательно дальше сторона BA, а потом сторона BC, т. К против неё наименьший угол BAC. AC — BA — BC.

Так как угол 1 = углу 2, то АОС — равнобедренный, = > АО = ОС Треугольники АОВ и СОВ равны по двум сторонам и углу между ними(ВО — общая ; АО = СО ; Угол 3 = Углу 4) Из этого следует, что АВ = ВС, следовательно АВС — равнобедренный.

Давление уменьшилось в 2 раза.

30 : 5 = 6 см отрезок МЕ. Так значит ДМ = 24 см.

Скрещивающиеся прямые не имеют общих точек. У прямых AD и AB — общая точка A. У прямых AD и BD — общая точка D. У прямых AD и CD — общая точка D. ПрямыеAD и BC — скрещивающиеся.

BD — медиана и высота значит треугольник ABC равнобедренный, AB = BC, AD = DC, AB + AD = PABD — BD = 15 — 4 = 11 см PABC = 2 * (AB + AD) = 11 * 2 = 22 см периметр треугольника ABC = 22 cм.

ВС = АВ + АС Х = 6 + 9 = 15 ВС = 15.

Т. к точка А делит отрезок ВС на два отрезка, то этот отрезок ВС равен сумме двух получившихся отрезков, т. Е ВС = АВ + АС = 6 + 9 = 15. Ответ : отрезок ВС равен 15 сантиметрах.

Видео:Геометрия. ОГЭ по математике. Задание 16Скачать

Касательная к окружности

О чем эта статья:

Видео:№1,17 | Все теория по планиметрии за 4 часа | Решаем все прототипы №1 из ФИПИСкачать

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

• окружность с центральной точкой А;
• прямая а — касательная к ней;
• радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Задача

У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°

Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.

Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.

Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.

Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.

∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).

Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МС = МВ — ВС = 16 — 12 = 4 (см)

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

(у + R) 2 : 4 = (у + R) × (у — R)

Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Ответ: MO = 10 см.

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.

АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°

📺 Видео

№661. Найдите острый угол, образованный двумя секущими, проведенными из точки, лежащейСкачать

Отрезки касательных из одной точки до точек касания окружности равны | Окружность | ГеометрияСкачать

№668. Докажите, что перпендикуляр, проведенный из какой-нибудь точки окружности к диаметру, естьСкачать

Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

ОГЭ по математике #17Скачать

№660. Через точку, лежащую вне окружности, проведены две секущие, образующие угол в 32Скачать