Геометрия | 5 — 9 классы
Из точки М к окружности проведены касательная MN(N – точка касания) и секущая MK, пересекающая окружность в точке Р так, что РМ длиннее РК на 2 и короче МN на 3.
Найдите длину отрезка касательной(MN).
OL = OK, какрадиусыоднойокружности, ΔLOK — равнобедренный, ∠OLK = ∠OKL = 38°
К. МN — касательная, значит
∠NMK = 180 — (90 + 38) = 52°.
- Из точки А проведены к окружности касательная AB и секущая ACD?
- Под прямым углом из точки А к окружности проведены две касательные ?
- Дана окружность с центром в точке О?
- Из одной точки проведены касательная и секущая касательная длиннее внешнего отрезка секущей на 5 см и короче внутреннего отрезка на строкой же Найдите касательну?
- Из точки E к окружности проведены касательная AE и секущая BE?
- К окружности с центром в точке О проведена касательная АК ( К — точка касания), домов отрезка АК равна √15?
- Из точки А, лежащей на окружности с центром в точке О, проведена касательная АS и секущая AR?
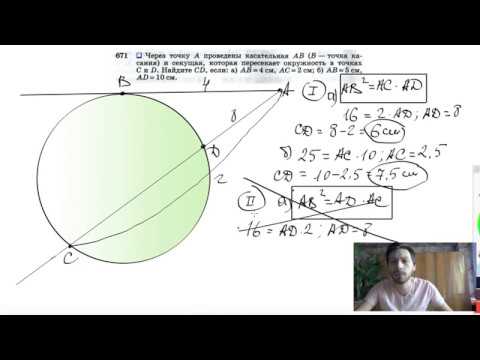
- Через точку а проведены две касательные ав(в — точка касания)и секущая, пересекающая окружность в точке с и е так, что а — с — е, ав = 10 см, ае = 20 см?
- К окружности с центром О проведены касательные BH и BK(H И k — точки касания)?
- Через точку А проведены касательная АВ, (В — Точка касания) и секущая, пересекающая окружность в точках С и К так, что АС = 4 см ; АК = 16 см?
- Из точки м к окружности проведены касательная мн
- Как написать хороший ответ?
- Касательная к окружности
- Касательная к окружности, секущая и хорда — в чем разница
- Свойства касательной к окружности
- Задача
- Задача 1
- Задача 2
- Задача 1
- Задача 2
- Задача 1
- Задача 2
- 🌟 Видео
Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

Из точки А проведены к окружности касательная AB и секущая ACD?
Из точки А проведены к окружности касательная AB и секущая ACD.
Во сколько раз отрезок секущей, лежащий внутри круга, больше отрезка секущей, находящегося вне круга, если расстояние от точки А до точки B в 3 раза больше, чем длина отрезка, лежащего вне круга.
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Под прямым углом из точки А к окружности проведены две касательные ?
Под прямым углом из точки А к окружности проведены две касательные .
Расстояние от точки А до цента окружности равно 2 см.
Найдите длину окружности.
Видео:8 класс, 32 урок, Касательная к окружностиСкачать

Дана окружность с центром в точке О?
Дана окружность с центром в точке О.
Отрезки секущей этой окружности проходящей через точки А и О равны, AP = 4 AQ = 16.
Найдите длину касательной АВ проведенной к данной окружности.
Видео:ОГЭ математика. Задание 16. Окружность. Касательная.Скачать

Из одной точки проведены касательная и секущая касательная длиннее внешнего отрезка секущей на 5 см и короче внутреннего отрезка на строкой же Найдите касательну?
Из одной точки проведены касательная и секущая касательная длиннее внешнего отрезка секущей на 5 см и короче внутреннего отрезка на строкой же Найдите касательну.
Видео:Отрезки касательных из одной точки до точек касания окружности равны | Окружность | ГеометрияСкачать

Из точки E к окружности проведены касательная AE и секущая BE?
Из точки E к окружности проведены касательная AE и секущая BE.
Эта секущая пересекает окружность в точках B и C.
Найдите длину AE, если BC = 5 см, BE = 4 см
С ЧЕРТЕЖОМ ПОЖАЛУЙСТА.
Видео:Геометрия Докажите, что если через точку A к окружности проведены касательная AM (M – точка касания)Скачать

К окружности с центром в точке О проведена касательная АК ( К — точка касания), домов отрезка АК равна √15?
К окружности с центром в точке О проведена касательная АК ( К — точка касания), домов отрезка АК равна √15.
Прямая АО пересекает окружность в точках В и С, причём АВ = 3.
Найдите диаметр окружности.
Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Из точки А, лежащей на окружности с центром в точке О, проведена касательная АS и секущая AR?
Из точки А, лежащей на окружности с центром в точке О, проведена касательная АS и секущая AR.
Найдите острый угол между касательной и секущей, если секущая равна радиусу окружности.
Видео:ОГЭ за одну минуту | ОГЭ, математика, задание 16 (окружность и касательная)Скачать

Через точку а проведены две касательные ав(в — точка касания)и секущая, пересекающая окружность в точке с и е так, что а — с — е, ав = 10 см, ае = 20 см?
Через точку а проведены две касательные ав(в — точка касания)и секущая, пересекающая окружность в точке с и е так, что а — с — е, ав = 10 см, ае = 20 см.
Найдите длину ас
Видео:Некоторые свойства окружности касательная к окружности - 7 класс геометрияСкачать

К окружности с центром О проведены касательные BH и BK(H И k — точки касания)?
К окружности с центром О проведены касательные BH и BK(H И k — точки касания).
Отрезки BO и KH пересекаются в точке С.
Найдите длину отрезка BK, если BC — 8, kh = 12.
Видео:ЕГЭ по математике. Задание №16 #11Скачать

Через точку А проведены касательная АВ, (В — Точка касания) и секущая, пересекающая окружность в точках С и К так, что АС = 4 см ; АК = 16 см?
Через точку А проведены касательная АВ, (В — Точка касания) и секущая, пересекающая окружность в точках С и К так, что АС = 4 см ; АК = 16 см.
На этой странице находится вопрос Из точки М к окружности проведены касательная MN(N – точка касания) и секущая MK, пересекающая окружность в точке Р так, что РМ длиннее РК на 2 и короче МN на 3?, относящийся к категории Геометрия. По уровню сложности данный вопрос соответствует знаниям учащихся 5 — 9 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Геометрия. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.
Решение на первое задание.
, цилиндр, квадрат, прямоугольник, ромб.
Основанием правильной четырёхугольной призмы является квадрат. Радиус вписанной в квадрат окружности равен половине его стороны : r = (1 / 2)a 1 = a / 2 a = 2 S(б) = Pосн * h = 2 * 4 * 1 = 8 (кв. Ед. ).
1) 180 — 90 — 37 = 53 2)180 — 90 — 32 = 58 3) угол А = 180 — 90 — 26 + 64 угол САК = 64 / 2 = 32 угол АКС = 180 — 90 — 32 = 58 7) так как, угол Е = 30, то ЕД = 2FD = 28 (против угла в 30 градусов лежит катет, равный половине гипотенузы) 8) А = 30 (то..
А b — длины сторон в сантиметрах 2а + 2b = 112 a = b + 12 — — — — — — упростим систему уравнений a + b = 56 a — b = 12 — — — — — — сложим первое ив второе 2a = 68 a = 34 см — — — — — — и теперь подставим найденное а a + b = 56 34 + b = 56 b = 22 см.
Т. к треугольник равнобедренный, то все стороны равны : AB = BC = AC = √8 Если в этом вопрос.
Опустим высоту СМ на основание АD. BC = AM MD = 9 — 6 MD = 3 Найдем угл DCM 180 — 60 — 90 = 30. Катет, леж. На против угла в 30°, будет равен половине гипотенузы. СD = MD * 2 CM = 3 * 2 CM = 6 Ответ : 6 ( вроде так).
Думаю рисунок труда не составит сделать, AD и BC основания трапеции опускаешь из точек B и C 2 высоты BH1 и CH2, H1H2 = 8. Далее из прямоугольных треугольников ABH1 и CH2D ищешь катеты AH1 и H2D AH1 = AB * cos60 = 10 * 1 / 2 = 5 H2D = CD * cos45 = 6..
17 : 2 = 8, 5 12 : 2 = 6 8, 5 + 6 = 14, 5см.
Видео:Урок по теме КАСАТЕЛЬНАЯ К ОКРУЖНОСТИСкачать

Из точки м к окружности проведены касательная мн
Вопрос по геометрии:
Из точки М к окружности проведены касательная MN и секущая МК, угол между этой секущей и радиусом OL равен 38°. Найдите величину угла NMK. Ответ дайте в градусах
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Видео:Радиус, проведенный в точку касания, перпендикулярен данной касательной. Доказательство. #геометрияСкачать

Касательная к окружности
О чем эта статья:
Видео:№658. Через точку А к данной окружности проведены касательная АВ (В — точка касания) и секущая ADСкачать
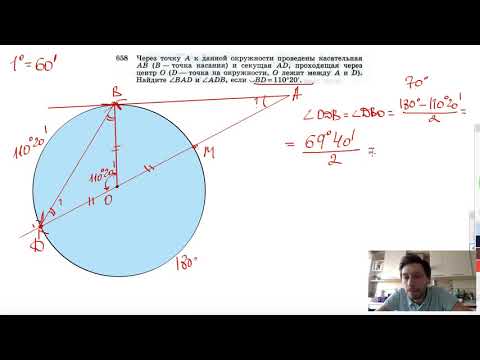
Касательная к окружности, секущая и хорда — в чем разница
В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.