Из одной точки к двум касающимся внешним образом окружностям

Видео:ОГЭ Задание 26 Внешнее касание двух окружностейСкачать

Ваш ответ

Видео:ЕГЭ задание 16Скачать

решение вопроса

Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,036
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Касающиеся внешним образом окружности и две общие касательные к нимСкачать

Задача 45619 Две касающиеся внешним образом в точке К.

Условие

Две касающиеся внешним образом в точке К окружности, радиус одной из которых вдвое больше радиуса другой, вписаны в угол с вершиной А. Общая касательная к этим окружностям, проходящая через точку К, пересекает стороны угла в точках В и С.

а) Докажите, что АВ = АС.
б) Найдите радиус окружности, описанной около треугольника АВС, если АВ = sqrt(3). [16п2]

Все решения

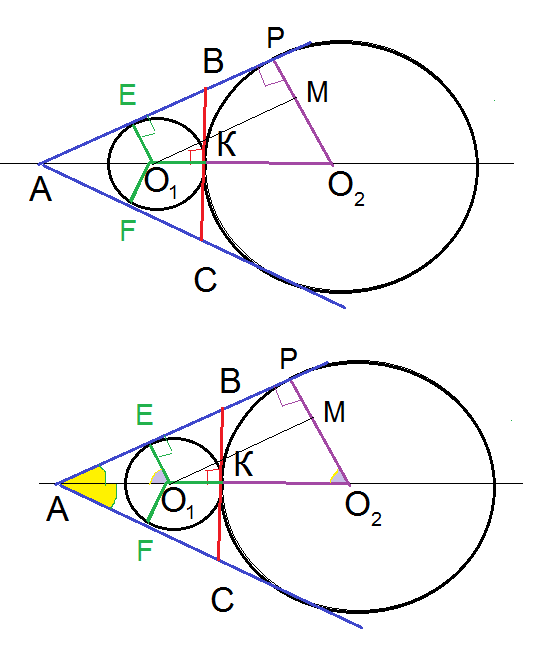
Две окружности вписаны в угол с вершиной А.
Радиусы O_(1)E и O_(1)F, проведенные в точки касания , [i]перпендикулярны [/i]сторонам угла.

По [i]свойству касательных[/i] к окружности, проведенных из одной точки, отрезки касательных равны:
[red]АE[/red]=[red]АF[/red]
и образуют [i]равные углы [/i]с прямой, проходящей через вершину А и центры окружностей.
Значит
центры O_(1) и O_(2) лежат на [i]биссектрисе[/i] угла А

BC — касательная к этим окружностям, проходящая через точку К,
значит О_(1)K ⊥ BC

AK — биссектриса и высота треугольника АВС, значит Δ АВС — равнобедренный и [b]АВ=АС[/b].

и AK — медиана Δ АВС ⇒ BK=CK

Прямоугольные треугольники
Δ AEO_(1)

Δ APO_(2) по двум углам
( ∠ EAO_(2)- общий)
⇒ [b]∠ АО_(1)E= ∠ AO_(2)P [/b]

O_(1)EPO_(2) — прямоугольная трапеция.
O_(1)E=r
O_(2)E=2r

Δ AEO_(1)= Δ O_(1)MO_(2) ⇒ [b] AO_(1)[/b]=O_(1)O_(2)=[b]3r[/b]

По теореме Пифагора из треугольника АВК

R=AB*BC*AC/4S_( Δ ABC)= AB^2/2AK=3/2sqrt(21/8)=sqrt(6/7)

О т в е т. [m]sqrtfrac[/m]

Видео:Задание 26 Две окружности, внешнее касаниеСкачать

Из одной точки к двум касающимся внешним образом окружностям

Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.

а) Докажите, что прямые AD и BC параллельны.

б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.

а) Обозначим центры окружностей O₁ и O₂ соответственно. Пусть общая касательная, проведённая к окружностям в точке K, пересекает AB в точке M. По свойству касательных, проведённых из одной точки, AM = KM и KM = BM. Треугольник AKB, у которого медиана равна половине стороны, к которой она проведена, — прямоугольный.

Вписанный угол AKD прямой, поэтому он опирается на диаметр AD. Значит, AD ⊥ AB. Аналогично получаем, что BC ⊥ AB. Следовательно, прямые AD и BC параллельны.

б) Пусть, для определенности, первая окружность имеет радиус 4, а радиус второй равен 1.

Треугольники BKC и AKD подобны, Пусть тогда

У треугольников AKD и AKB общая высота, следовательно, то есть S_AKB = 4S. Аналогично, S_CKD = 4S. Площадь трапеции ABCD равна 25S.

Вычислим площадь трапеции ABCD. Заметим, что Проведём к AD перпендикуляр O₂H, равный высоте трапеции, и найдём его из прямоугольного треугольника O₂HO₁:

Тогда

Следовательно, 25S = 20, откуда S = 0,8 и S_AKB = 4S = 3,2.

Приведем вариант решения п. б) предложенный Рамилем Багавиевым.

Из первого решения известно, что Из подобия треугольников AKD и AKB следует таким образом AK = 2BK. Напишем теорему Пифагора для треугольника AKB

Теперь несложно вычислить

Критерии оценивания выполнения задания	Баллы
Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б)	3
Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки	2
Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, 🔍 Видео ТОП-3 конструкции с окружностями для №16 из ЕГЭ 2023 по математикеСкачать ОГЭ задание 26Скачать Три окружности касаются прямой и друг друга внешним образомСкачать ОГЭ. Понятный разбор задачи №26. Две окружности радиусов 44 и 77 касаются внешним образом...Скачать Геометрия Окружность радиуса 4 касается внешним образом второй окружности в точке B. ОбщаяСкачать Две окружности соприкасаются внешним образом. к ним...Задача.Скачать Пара касающихся окружностей | Осторожно, спойлер! | Борис Трушин |Скачать Математика ОГЭ Геометрия Задача 25 внешнее касание окружностейСкачать Построение касательной двум окружностям внешнего касанияСкачать 1 2 4 сопряжение окружностейСкачать ОГЭ № 25. "Окружности касаются внешним образом... "Скачать ЕГЭ Задание 16 Две касающиеся окружностиСкачать Внешняя касательная к двум окружностямСкачать Задача поколения ЕГЭСкачать Построение внешней касательной к двум дугам окружностей. Урок11.(Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать 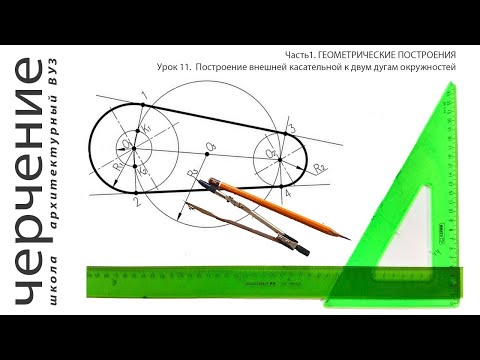Поделиться или сохранить к себе: Смотрите также Ящик тянут по земле по горизонтальной окружности длиной 60 Ящик тянут по земле по горизонтальной окружности длиной 40 Ящик тянут по земле по горизонтальной окружности диаметром 20 Ящик тянут по земле за веревку по горизонтальной окружности длиной Ящик тянут по земле за веревку по горизонтальной окружности диаметром Электрон равномерно движется по окружности в однородном магнитном поле Электрон и протон ускоренные разностью потенциалов движутся по окружности Шарик скатывается по желобу изогнутому в виде дуги окружности