Использование треугольников в строительстве

Каких только правил не применяют начинающие строители, возводя дома или бани на своих участках. Но зачастую такие «потуги» сделать всё идеально приводят к противоположному результату. И дело даже не в том, что используемый способ не работает в принципе. Чаще домашние мастера сами до конца не понимают, для чего выполняется то или иное действие. В сегодняшней статье речь пойдёт об одном из способов разметки под фундамент, пришедшем из древних времён – «египетском треугольнике».

Видео:Угольник Свенсона. 7 функций в домашних условиях.Скачать

Что такое «египетский треугольник», и откуда он появился

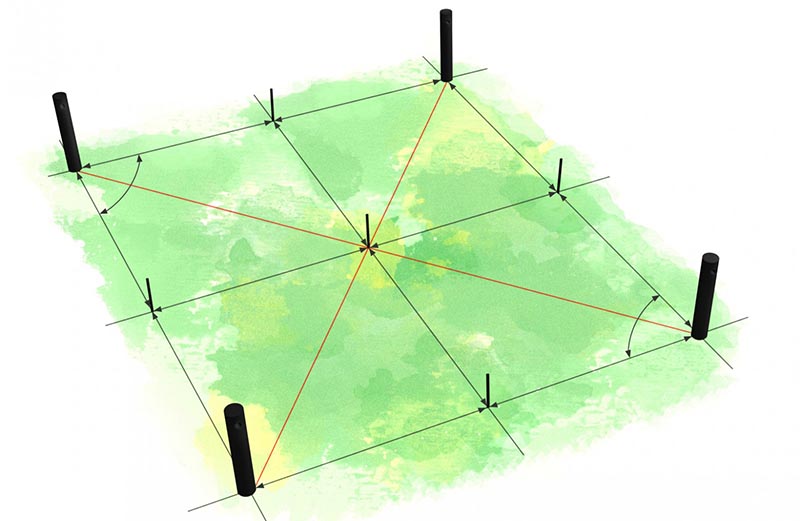
Придумали подобный способ замеров не древние египтяне, как могло бы показаться, судя по названию. На самом деле таким методом разметки пользовались строители ещё задолго до появления пирамид. Суть метода заключается в том, чтобы разделить квадрат будущего строения на два одинаковых треугольника со сторонами, относящимися друг к другу как 3:4:5.

Это должен быть прямоугольный треугольник, подчиняющийся теореме Пифагора. Наверняка все помнят её из школьной программы – сумма квадратов катета равна квадрату гипотенузы, и наоборот. Логически при совмещении этих треугольников должен получиться квадрат с идеально одинаковыми диагоналями. И вот тут начинается самое интересное.

Видео:Что такое египетский треугольник?Скачать

Глупая ошибка строителей

«Египетский треугольник» действительно может помочь в разметке периметра фундамента, однако применение этого метода требует сохранения чётких пропорций. Небольшое отклонение от них − и угол уже не будет прямым. А это приведёт к разнице длин стен. Не единичны случаи, когда при идеальном совпадении длин диагоналей стены получаются разными. Ведь если вдуматься, то трапеция также подходит под заданные параметры, её диагонали равны, в то время как верхняя и нижняя сторона имеют разные длины.

ФОТО: youc.ir Правильная трапеция также имеет одинаковые длины диагоналей, однако на квадрат она явно не тянет

Видео:Треугольник в строительствеСкачать

Как быть, если строение не подходит под размер 3×4

Понятно, что если стороны дома не подходят под заданный размер, придётся производить вычисления. Но здесь всё не так уж и сложно. К примеру, необходимо построить здание, размеры которого больше. Тогда можно сделать одну стену длиной 12 м, а вторую − 15 м. В этом случае, пользуясь всё той же теоремой Пифагора и особенностями «египетского треугольника», несложно вычислить необходимую длину диагонали (она же гипотенуза), которая будет равна 19,2 м.

ФОТО: fsks.ru Все углы разметки под фундамент должны быть идеально прямыми – это аксиома

«Египетский треугольник» − это способ разметки, используемый в строительстве с незапамятных времён. И то, что он и сейчас достаточно популярен, говорит о работоспособности метода. Главное – использовать его на полную, а не обходиться только поверхностными знаниями.

ФОТО: tvoidom-msk.ru Лучше потратить немного больше времени и вывести углы фундамента, чем впоследствии получить массу проблем при строительстве и отделке

Видео:Египетский треугольник. Пифагоровы тройки.Скачать

Другие размеры стен и применение к ним правила «египетского треугольника»

На самом деле, если разобраться с тем, как «работает» «египетский треугольник», можно вывести стены различной длины. Главное – это их соотношение друг с другом. Попробуем разобрать этот момент на примере.

Требуется, чтобы одна из стен была равна восьми метрам. Для того чтобы соотношение получилось верным, вторую стену нужно сделать длиной 6 м. В этом случае число 8 можно обозначить как 4 отрезка по 2 м, а 6 – как 3 отрезка по 2 м. Разобравшись с длиной стен, можно свободно вывести и длину диагонали, которая будет равна квадратному корню из 6×6+8×8 (квадратный корень из 100). Получается, диагональ должна быть равна 10 м. Всё крайне просто.

ФОТО: warfields.ru Можно использовать любые размеры, главное, чтобы они имели правильное соотношение

Видео:Мало кто знает об этих скрытых функциях УГОЛЬНИКА! ТАКОГО ТЫ ЕЩЕ НЕ ВИДЕЛ!Скачать

Иные способы выведения прямого угла

Если нет желания заниматься выведением углов самостоятельно, а финансы позволяют обратиться за помощью к специалистам, можно вообще не думать об этом вопросе. Один звонок − и на участке уже находится геодезист с теоделитом, который в сжатые сроки сделает разметку. Однако в этом случае необходимо быть готовым к внушительным затратам на оплату его труда.

ФОТО: omegagalvanoplastia.com.br Теоделит – высокоточная техника, однако стоимость подобной разметки может влететь «в копеечку»

Если говорить о минимальных затратах, то, основываясь на прайс-листах фирм, оказывающих подобные услуги, вызов и работа геодезиста с инструментом обойдётся в 1 000 руб./час при минимальной оплате 7 000 руб. Дальше − больше. Разметка осей (2 точки) – ещё 3 000 рублей. Если же потребуется определить точные координаты по GPS, то здесь каждые три точки обойдутся владельцу в 5 000 руб. Можно посчитать, какова будет общая сумма (все цены указаны с учётом на конец сентября 2020 года). Не проще ли самому произвести все необходимые разметки? Ведь сэкономленные средства всегда можно потратить на что-то полезное в дальнейшем строительстве.

ФОТО: thelundreport.org Стоит приготовиться к тому, что карман значительно облегчится

Видео:Как узнать прямой угол с помощью рулетки. Египетский треугольник в строительствеСкачать

Заключительное слово

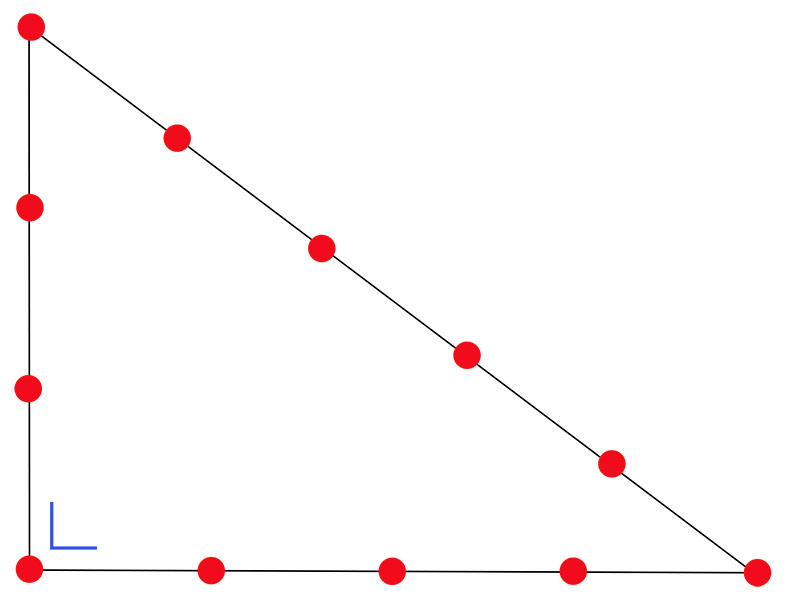
Что бы ни говорили противники описанного метода измерений, но «египетский треугольник» в значительной степени помогает строителям в выведении прямых углов. Конечно, при условии его правильного использования. Тем более что навязать 12 узлов на верёвке на определённом расстоянии один от другого много времени не потребует. Также это не потребует и финансовых затрат, связанных с наймом геодезиста с необходимым оборудованием.

ФОТО: profipol.dp.ua Так должны быть расположены узлы на верёвке для построения «египетского треугольника»

Очень надеемся, что сегодняшняя статья была полезна нашему уважаемому читателю и дала общее представление о «египетском треугольнике» и его применении. Если у вас по ходу ознакомления с предоставленной информацией возникли вопросы, редакция онлайн-журнала Homius будет рада на них ответить. Вам лишь нужно изложить суть в комментариях ниже. Там же можно обсудить, стоит ли пользоваться методами, проверенными временем, или давно пора о них забыть и перейти к более высокотехнологичным приспособлениям. Если статья понравилась, не забывайте ставить оценки. А мы напоследок предлагаем вашему вниманию короткий видеоролик, который поможет более полно раскрыть сегодняшнюю тему. Берегите себя, своих близких и будьте здоровы!

Видео:Скрытые возможности обычного угольника! А вы их знали?Скачать

Что такое Египетский треугольник на стройке? В чем его особенность +Фото и Видео

Строительство с применением египетского треугольника древний способ, активно используемый до сих пор современными строителями. Название получил благодаря древнеегипетским сооружениям, хотя известно, что история его начинается задолго до этого периода.

Но, скорее всего, свойства уникальной фигуры не были оценены в те времена, пока не появился Пифагор, сумевший проанализировать и оценить изящные формы фигуры.

Египетский треугольник известен еще с древних времен. Он был и остается популярен в строительстве и архитектуре много веков.

Считается, что создал геометрическую конструкцию великий греческий математик Пифагор Самосский. Благодаря ему сегодня мы можем использовать все свойства геометрической постройки в области строения.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Египетский треугольник в строительстве. Общие сведения

Зарождение идеи

Идея у математика появилась после путешествия в Африку по просьбе Фалеса, который поставил задачу Пифагору изучить математику и астрономию тех мест. В Египте он среди бескрайней пустыни встретил величественные строения, поразившие его размером, изяществом и красотой.

Надо заметить, что более двух с половиной тысяч лет назад пирамиды были несколько другими – огромными, с четкими гранями. Тщательно изучив могущественные постройки, коих было не мало, так как рядом с великанами, стояли храмы поменьше, построенные для детей, жен и других родственных лиц фараона, это натолкнуло его на мысль.

Благодаря своим математическим способностям, Пифагор сумел определить закономерность в формах пирамиды, а умение анализировать и делать выводы привели к созданию одной из самых значимых теорий в истории геометрии.

Из истории

Знали ли в древнем Египте о геометрии и математике? Конечно да. Жизнь египтян была тесно связана с наукой. Они регулярно пользовались знаниями при разметке полей, создании архитектурных шедевров. Даже существовала своя служба землемеров, которые применяли геометрические правила, занимаясь восстановлением границ.

Название треугольник получил благодаря эллинам, которые нередко бывали в Египте в VII-V вв. до н.э. Считается, что прообразом фигуры стала пирамида Хеопса, отличающаяся совершенными пропорциями. Ее место особенное в истории. Если посмотреть поперечное сечение, то можно отметить два треугольника, у которых угол внутри равняется 51 о 50’.

Строение

Сегодня это строение усеченной формы, приобретенной под воздействием времени, высота явно потерялась. Однако, восстановив ее геометричность, можно сделать вывод, что стороны треугольников равны. Получается в основе заложен золотой прямоугольный треугольник.

Однако, следует рассмотреть другую пирамиду – Хефрена, у которой основа как раз-таки прямоугольный треугольник и где угол наклона боковых граней равен 53 о 12 с соотношением катетов 4:3. Это уже так называемый священный треугольник. Для египтян такая фигура сопоставлялась с семейным очагом: катет вертикального положения олицетворял мужчину, основание – представительницу прекрасного пола, а гипотенуза – рождение ребенка от обоих.

Стороны пирамиды Хефрена в соотношении равны 3:4:5, что точно соответствует теореме Пифагора. Значит, можно сделать вывод, что строители уже знали об этой теореме, но не могли ее сформулировать. Хотя, в исторических письменах встречаются следы использования египетского треугольника за много веков даже до Египта. До сегодняшнего дня это загадка, как могли такие знания получить древние египтяне. Понимали ли они чем обладают?

Особенность фигуры к тому же в том, что благодаря подобному соотношению, она является простым и первым Героновым треугольником, так как ее стороны и площадь целочисленные.

Обратное доказательство

Как доказать, что треугольник прямоугольный? Нужно порой исходить от обратного, то есть если сумма квадратов обеих сторон равна квадрату третьей, то треугольник прямоугольный, что подтверждает равенство 3 2 х4 2 =5 2 и значит он действительно прямоугольный.

Таким образом теорема Пифагора стала каноном и фундаментом развития математической науки. Со школьной скамьи каждый ученик знает, что означает выражение «Пифагоровы штаны во все стороны равны».

Интересно, что теорема Пифагора находится в Книге Гиннесса как теорема, обладающая самым большим количеством доказательств, которых примерно 500.

Особенности

Если рассмотреть более детально отличительные особенности египетского треугольника, то можно выделить следующие моменты:

• все стороны и площадь состоят из целых чисел, как говорилось выше;
• согласно теории великого математика, сумма квадратов катетов равна квадрату гипотенузе;
• такой фигурой возможно отмерить прямые углы в пространстве. Это используется в процессе строительства до сих пор;
• не обязательно пользоваться специальными измерительными приборами, подойдут подручные средства, например, веревка.

Видео:Swanson. Угольник Свенсона. Как использовать? Serhulya TVСкачать

Место в строительном мире

С древнейших времен египетский треугольник нашел почетное место в архитектуре и строительстве. Конструкция пирамиды отличается тем, что позволяет создавать здание с совершенно правильными углами без каких-либо дополнительных инструментов.

Задача намного облегчается, если использовать транспортир или треугольник. Но, раньше применялись только шнуры и веревке, разделенные на отрезки. Благодаря отметкам на веревке можно было с точностью воссоздать прямоугольную фигуру. Строителям заменяла транспортир и угольник веревка, для чего отмечали узлами на ней 12 частей и складывали треугольник с отрезками 3,4,5. Прямой угол получался без затруднений. Эти знания помогли создать множество сооружений, в том числе пирамиды.

Интересно, что до древнего Египта, таким способом строили в Китае, Вавилоне, Месопотамии.

Свойства египетской треугольной фигуры подчиняются истине – квадрат гипотенузы равен квадратам двух катетов. Эта теорема Пифагора знакома каждому со школьной поры. Например, умножаем 5х5 и получаем гипотенузу равную числу 25. Квадраты обоих катетов равны 16 и 9, что в сумме дает цифру 25.

Благодаря таким свойствам, треугольник нашел применение в строительстве. Можно взять любую деталь, с целью провести линию прямого направления с условием, что ее длина должна быть кратной пяти. После этого заметить один край и прочертить от него линию кратную четырем, а от другого кратную трем. При этом каждый отрезок должен быть длиной минимум четыре и три. Пересекаясь, они образовывают один прямой угол в 90 градусов. Другие углы равны 53,13 и 36,87 градусам.

Видео:Фермы и мостыСкачать

Какие существуют альтернативные варианты

Как создать прямой угол

Лучшим вариантом смастерить прямой угол является применение угольника или транспортира. Это позволит с минимальными затратами найти необходимые пропорции. Но, основной момент египетского треугольника в его универсальности из-за возможности создать фигуру, не имея под рукой ничего.

В этом деле может пригодиться все, даже печатные издания. Любая книга или даже журнал имеют всегда соотношение сторон, образующее прямой угол. Типографские станки работают всегда точно, чтобы рулон, заправленный в машину резался пропорциональными углами.

Древние инженеры придумывали много способов строительства египетского треугольника и всегда экономили ресурсы.

Поэтому, самым простым и широко применяемым был метод постройки геометрической фигуры с применением обычной веревки. Бралась бечевка и резалась на 12 ровных частей, из которых выкладывалась фигура с пропорциями 3,4 и 5.

Как создать другие углы?

Египетский треугольник в строительном мире нельзя недооценивать. Его свойства однозначно полезны, но без возможности построить углы другого градуса в строительстве невозможно. Чтобы образовался угол в 45 градусов, понадобится рамка или багет, которые распиливаются под углом в 45 градусов и соединяются между собой.

Важно! Чтобы получить необходимый наклон, потребуется позаимствовать бумажный лист из печатного издания и согнуть его. Линии изгиба при этом будут проходить через угол. Края должны быть соединены.

Получить 60 градусов можно с применением двух треугольников по 30 градусов. Чаще всего используются для создания декоративных элементов.

Видео:Угольник Свенсона - максимальный обзор (Swanson Speed Square - How To Use)Скачать

Небольшие хитрости

Египетский треугольник 3х4х5 актуален для маленьких домов. Но, что делать, если дом 12х15?

Для этого нужно построить прямоугольный треугольник, у которого катеты равняются 12 и 15 м. Гипотенуза находится как квадратный корень из суммы 12х12 и 15х15. В итоге получаем 19,2 м. С помощью чего-либо — веревки, шпагата, бечевки, тросика, военного кабеля, отмеряем 12, 15 и 19,2 м. Делаем узлы на этих местах и ставим жимки.

Затем треугольник нужно растянуть на нужном месте и установить 3 точки опоры, в которые вбить колышки. Четвертую точку можно получить, не трогая концы катетов. Для этого точка прямого угла перекидывается по диагонали и все готово.

Например, есть участок, где требуется прямой угол – для места под кухонный гарнитур, раскладки кафеля и других моментов. Хорошо бы такие вопросы учесть при кладке, но реальность другая и не всегда попадаются ровные стены и прямые углы. Здесь пригодится египетский треугольник с соотношением 3:4:5, либо при необходимости 1,5:2:2,5.

Обязательно учитывается толщина маяков, погрешность, бугры на стенах и т.д. Треугольник рисуется с помощью рулетки и мела. Если разметка небольшая, то можно воспользоваться листом гипсокартона, так как режутся они с правильными углами.

Египетский треугольник широко использовался в строительстве целых 2,5 века. И сегодня иногда приходится применять данную методику, при отсутствии необходимых инструментов, чтобы получить прямые углы. Свойства этой фигуры уникальны, что гарантирует точность в архитектуре и строительстве, без которой не обойтись. С ним легко работать, по форме он гармоничен и красив. До сих пор пытливые умы пытаются разгадать тайну египетского треугольника.

Видео:ошибки при строительстве прудов. Строим,проектируем пруды +996559777111 вотсапСкачать

Проект «Исследование жёсткости треугольника» (7 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Исследование жесткости треугольника.docx

Исследование жесткости треугольника

Понятие «жесткость треугольника» 4

Разнообразный мир треугольников или где в жизни встречается треугольник? 4

Применение свойства жесткости треугольника на практике 7

Применение треугольника в жизни человека 8

Список использованных источников информации 11

В этом учебном году мы начали изучать новый предмет – геометрию – науку, занимающейся изучением геометрических фигур. Основная фигура, которую изучаем мы в геометрии 7 класса – это треугольник. Познакомившись с признаками равенства треугольников, мы узнали о таком понятии как жесткость треугольника, и нам захотелось больше узнать об этом свойстве. И мы решили попробовать понять, и раскрыть особенности применения этой фигуры в жизни человека.

Как оказалось, это свойство треугольника широко используется в практической жизни. И значит, данная тема продолжает оставаться актуальной с древнейших времен.

Цель работы: установить, что треугольник – жесткая фигура, которая нашла широкое практическое применение в жизни человека.

1. Верно ли, что треугольник жёсткая фигура?

2. Нужно ли свойство жёсткости треугольника в жизни человека?

Изучить литературу о треугольнике

Исследовать применение свойства жесткости на практике

Проанализировать применение треугольника в жизни человека

Обобщить собранную информацию и познакомить с ней своих одноклассников.

Гипотеза: треугольник является жесткой фигурой, данное свойство широко используется в жизни человека.

Практическая значимость: обобщённый материал данного исследования можно применять как на уроках математики, так и во внеурочное время для привития интереса к математике. Данный материал способствует формированию представления о прикладных возможностях математики.

Понятие «жесткость треугольника»

Рассмотрим модели двух фигур — треугольника и четырёхугольника и выясним, можно ли, не меняя длины сторон, изменить форму фигуры? Проверим это опытным путём. Представим себе две рейки, у которых два конца скреплены гвоздем. Такая конструкция не является жёсткой: сдвигая или раздвигая свободные концы реек, мы можем менять угол между ними.

Теперь возьмем еще две рейки, у которых два конца скреплены гвоздем, и соединим с имеющейся конструкцией. Получим четырехугольник.

В ней можно сдвинуть или раздвинуть две стороны, при этом четырехугольник меняет свою форму. Этозначит, что четырехугольник – не жёсткая фигура.

Теперь возьмем одну рейку и скрепим её концы со свободными концами первых двух реек. Полученная конструкция — треугольник . В ней нельзя сдвинуть или раздвинуть никакие две стороны, т. е. нельзя изменить ни один угол. Почему это происходит? Это происходит потому, что треугольник- жёсткая фигура. Жесткость треугольника вытекает из третьего признака равенства треугольников: если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.

Действительно, если бы это удалось, то мы получили бы новый треугольник, не равный исходному. Но это невозможно, так как новый треугольник должен быть равен исходному по третьему признаку равенства треугольников.

То есть можно сказать, что треугольник – не изменяющаяся фигура или жесткая фигура. В нем нельзя сдвинуть или раздвинуть никакие две стороны, в отличие от любого другого многоугольника. В треугольнике нельзя изменить ни один из углов. Таким образом, треугольник – жесткая фигура.

Разнообразный мир треугольников или где в жизни встречается треугольник?

Изображения треугольников и задачи на треугольники встречаются во многих папирусах Древней Греции и Древнего Египта. Еще в древности стали вводить некоторые знаки обозначения для геометрических фигур. Древнегреческий ученый Герон (I век) впервые применил знак вместо слова треугольник.

Треугольник является одной из первых геометрических фигур, которая стала использоваться в орнаментах древних народов.

С помощью натянутых веревок длиной 3, 4 и 5 единиц египетские жрецы получали прямые углы при возведении храмов и т.п. (Приложение №1)

Изображения и применение треугольников в и настоящее время встречаются практически везде.

Семья : мама, папа и ребенок.(Приложение №2)

Треугольники в природе . В природе встречаются растения, листья которых имеют форму треугольника. Это такие растения, как:Кариота ( Caryota ) – «Рыбий хвост». Эту пальму можно разводить только в помещении. Её листья напоминают удлинённые треугольники с оборванными широкими концами, похожими на плавники рыбы. Все виды, а их свыше 25, завезены из Юго-Восточной Азии. (Приложение №3)

Треугольники в одежде . Предметы одежды человека. Различные головные уборы: треуголки, пилотки, колпаки, косынки – имеют треугольную форму. Женские платки, прежде чем накинуть на голову, складывают пополам. При шитье юбки часто втачивают клинья, которые тоже имеют форму треугольника, что придает юбке пышность. Чтобы одежда не помялась, ее хранят на плечиках, имеющих треугольную форму. (Приложение №4 )

Треугольники в истории.

Солдатский треугольник — письмо без марки и конверта, отправленное солдатом с фронта или солдату на фронт.

Французский император Наполеон Бонапарт был любителем математики. Он находил время заниматься ею для собственного удовольствия, чувствовал в ней красоту и объект, достойный приложения остроумия и изобретательности. Одно из свидетельств тому — несколько составленных им геометрических задач.

Одна из задач Наполеона касается треугольника и звучит так: «Если на каждой стороне произвольного треугольника построить по равностороннему треугольнику, то треугольник с вершинами в центрах равносторонних треугольников — тоже равносторонний». (Приложение №5)

Треугольники в географии . Известен всем такой географический объект, в названии которого встречаем треугольник — Бермудский треугольник.Бермудский треугольник иногда называют еще дьявольским треугольником. Это район в Атлантическом океане, в котором происходят якобы таинственные исчезновения морских и воздушных судов. Район ограничен линиями от Флориды к Бермудским островам, далее к Пуэрто-Рико и назад к Флориде через Багамы. Выдвигаются различные гипотезы для объяснения этих исчезновений, от необычных погодных явлений до похищений инопланетянами.(Приложение №6)

Треугольник в астрономии . Треуго́льник — созвездие северного полушария неба, содержит 25 звезд, видимых невооружённым глазом. (Приложение №7)

Треугольник в архитектуре . Различные жилища людей: вигвам, юрта, палатка. Все они имеют конусообразную форму, в сечении получается треугольник. Такие сооружения легко обдуваются ветрами, с них быстро стекает вода. Крыши старых деревянных домов и современных многоэтажек имеют форму треугольника. Это связано с тем, что на таких крышах не задерживается талый снег и легко стекает дождевая вода.(Приложение №8)

Треугольник в строительстве.

Треугольники встречаются в конструкции железнодорожных мостов . Треугольники делают надежными конструкции высоковольтных линий электропередач. Для составления красивых паркетов чаще всего использовали треугольники.

Треугольник в искусстве. Флористика — это один из видов визуального искусства, в котором художник вместо красок пользуется лепестками цветов, их листиками, травами, где с помощью цветов создаётся эстетический образ, наполненный содержанием.Изящество, изысканность, очарование – и это далеко не всё, что приходит на ум при взгляде на цветочные творения.

При создании букета или композиции нужно соблюдать гармонию цвета. При этом используется метод равностороннего треугольника.Существуют три основных цвета: красный, жёлтый и синий, которые располагаются в вершинах треугольника, все остальные цвета получаются при смешивании основных цветов: к+ж=о, ж+с=з, с+к=ф.(Приложение №9)

При создании букета или композиции учитывается и форма букета. И здесь мы опять встречаемся с треугольником, например: композиция Европейской аранжировки «Высокий треугольник с элементами быта», « Французский высокий треугольник».(Приложение №10)

Треугольник в музыке.

Треуго́льник — ударный музыкальный инструмент в виде металлического прута , изогнутого в форме треугольника. Один из углов оставлен открытым (концы прута почти касаются).

Невозможный треугольник . Треугольник Пенроуза -невозможный объект. Плоский рисунок может обманывать, изображая невозможное.Закройте одну из вершин этого треугольника, и станет ясно, что одна из его сторон направлена к нам, а другая от нас, в пространстве они не могут соединиться. 13-метровая скульптура невозможного треугольника из алюминия была воздвигнута в 1999 году в городе Перт (Австралия).

Начиная игру в бильярд , необходимо расположить шары в виде треугольника. Для этого используют специальное приспособление.(Приложение №11)

Расстановка кеглей в игре Боулинг тоже в виде равностороннего треугольника.(Приложение №12)

Более 30 наименований и можно продолжать и продолжать. Рассматривая термин, треугольник в окружающем нас мире мы увидели, что математика часть общечеловеческой культуры и мир геометрии – увлекателен и интересен.

Применение свойства жесткости треугольника на практике

Своё исследование мы начали с анкетирования .В анкетирование приняло участие 24 человека, им были предложены вопросы:

Какая фигура самая жесткая?

Ответы: 3 ч. – квадрат, 4ч. – прямоугольник, 1ч. – круг, 16ч. – треугольник.

Знаете ли вы, где применяется свойство жесткости треугольника?

Ответы: да – 7ч, нет – 17ч.

Что в жизни вы встречали в форме треугольника?

Ответы: крыша, дорожный знак, платок, настольный календарь, салфетка и др.(Приложение №13)

После проведенного опроса, мы сделала вывод, что ребята не совсем знают применение свойства жесткости треугольника на практике. Тогда мы решили более подробно исследовать данный вопрос и ознакомить ребят с результатами.

Символ Франции знаменитая Эйфелева башня («Железная леди») — самая узнаваемая архитектурная достопримечательность Парижа. (Приложение №14)

Собрана она из более 12000 металлических деталей. Высота башни 300 метров, что делало её высочайшим строением в мире на протяжении 40 лет. Вес металлической конструкции 10 100 тонн. Колебания башни во время бурь не превышают 15 см. Это объясняется тем, что вся конструкция башни сплетена из треугольников, обладающих жёсткостью.

Сегодня вышка используется в интересах телевидения, радиовещания и сотовой телефонии.

При строительстве любых мостов в их конструкциях также присутствуют треугольники. Например, Железнодорожный мост «Эдуарда VII » в Ньюкасле, Мост «25 апреля» в Португалии и QuebecBridqePont — deQu . (Приложение №15)

Во время Великой Отечественной войны для сохранения стекол во время бомбежки их заклеивали бумажными полосками, чтобы получился треугольник.

Обладатели загородных участков, всегда стараются украсить свой сад. А если необходимо установить теплицу, то почему бы не сделать её украшением всего двора.

Недавно, большое распространение получили геодезические теплицы, состоящие из треугольников. Они красивы, просты, удобны и мобильны. Их можно легко разобрать и собрать. Затратив немного времени на сооружение подобной теплицы, вы получаете настоящую красоту, которая будет привлекать всех гостей. (Приложение №16)

Геодезический купол — это каркас конструкции, который держит оболочку. Благодаря своей форме, геодезические теплицы не восприимчивы к агрессивному поведению внешней среды. Они прекрасно переносят сильные ветра, землетрясения и большие снегопады. Также, внутри купола сохраняется постоянная температура, а её каркас позволяет сэкономить внешнее пространство на 30 процентов.

Насколько известно, треугольник – это самая прочная и устойчивая фигура. А геодезический купол как раз состоит из треугольников. Основной плюс всей конструкции, это её быстрый монтаж и демонтаж. Главное это правильно нарезать материал. Например, если вы используете поликарбонат, все детали должны быть одинаковой длины. Только так можно гарантировать простую сборку конструкции.

Мы решили проанализировать – встречается ли свойство жесткости треугольника в повседневной жизни, в моем городе. Для этого мы провели практическую работу , наблюдение.

Так, чтобы закрепить столб в вертикальном положении, к нему ставят подпорку. Телеграфные столбы с подпоркой называют анкерными.

Делая садовую калитку, обязательно прибивают планку, чтобы получить треугольник. Это придаёт калитке прочность, иначе её перекосит.

При строительстве любых мостов в их конструкциях также присутствуют треугольники.

Треугольники делают надежными конструкции высоковольтных линий электропередач.

Жесткость треугольников применяется при строительстве подъемных кранов.

Свойство жесткости треугольника широко используют в практике при строительстве железных конструкций.

Стропила зданий, леса строительные имеют вид треугольников. Это придаёт им крепость и устойчивость.(Приложение №1 7 )

Свойство жесткости треугольника нашло широкое применение в жизни человека. Наиболее часто данное свойство встречается при установке столбов и строительстве металлических конструкций.

Применение треугольника в жизни человека

Мы решили проанализировать – где можно встретить треугольник в нашем городе, районе.

Так как треугольник — одна из простейших фигур, то и употребляется она часто.

1.Треугольник можно увидеть в окружающей нас природе.

2. Стрелка. А вернее, ее наконечник.

3. Журавлиный клин

7. Элементы одежды

8. Уши животных(Приложение №1 8 )

Более подробно мы решили рассмотреть использование треугольника

В условных обозначениях на картах.

На дорожных знаках.(Приложение №1 9 )

Вмире можно найти много чего треугольной формы или очень похожей на нее. В повседневной жизни треугольник чаще всего встречается на дорожных знаках, крышах домов.

🎦 Видео

Большой и точный угольник за 10 минут. Египетский треугольникСкачать

8 класс, 27 урок, Практические приложения подобия треугольниковСкачать

Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Измерение угла с помощью транспортираСкачать

Высота прямоугольного треугольникаСкачать

Разбор фигуры Треугольник: технический анализ и правила торговлиСкачать