Использование признаков равенства треугольников

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

.Муниципальное автономное общеобразовательное учреждение

«Средняя общеобразовательная школа № 1»

Наименование секции/подсекции: математика/ точные науки

Исследовательская работа: Признаки равенства треугольников и их применение в практической деятельности человека

Авторы работы: Занозина Александра Ивановна, 7 Б класс, Шаньгина Екатерина Борисовна, 7 Б класс

Руководитель работы: Ельшина Наталья Викторовна, учитель математики, 89041682163, n . tchesnokowa 2013@ yandex . ru

Видео:7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Оглавление

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Введение

В этом учебном году мы начали изучать новый предмет – геометрия – наука, занимающаяся изучением геометрических фигур. Основная фигура, которую изучают в геометрии 7 класса – это треугольник. Один мудрец сказал: «Высшее проявление духа — это разум. Высшее проявление разума — это геометрия. Клетка геометрии — треугольник. Он так же неисчерпаем, как и Вселенная».

Треугольник в геометрии играет особую роль. Без преувеличения можно сказать, что почти вся геометрия строится на треугольнике. За несколько тысячелетий геометры столь подробно изучили треугольник. Первые упоминания о треугольнике и его свойствах ученые находят в египетских папирусах, которым более 4000 лет. Треугольник неисчерпаем – постоянно открываются его новые свойства. Чтобы рассказать обо всех известных его свойствах, необходим том сравнимый по объему с томом Большой энциклопедии.

При решении задач используют его самые разнообразные свойства. Свойства треугольника широко применяют на практике. Например, в архитектуре: при разработке чертежа здания, при планировке будущих квартир; в промышленности: при проектировании различны деталей, при изготовлении стройматериалов, при строительстве морских и авиа судов; в навигации: для прокладывания правильного и максимально точного маршрута; треугольники делают надежными конструкции высоковольтных линий электропередач и железнодорожных мостов; в астрологии и астрономии, одним словом, просто необходимо знать треугольник и все его свойства.

Актуальность. Мы слышим от старшеклассников и учителя, что при подготовке к сдаче экзамена по математике приходится доказывать равенство треугольников. Познакомившись с признаками равенства треугольников, мы узнали и о таком понятии как жесткость треугольника. После изучения трех признаков равенства треугольников, наш учитель сказала, что это не единственные признаки равенства треугольников и некоторые признаки равенства треугольников можно использовать в деятельности человека, и об этом знали еще в далекой древности. Нам захотелось узнать, а какие еще есть признаки равенства треугольников и можно ли какие-либо признаки использовать в практической деятельности человека.

Рассмотрев учебник по геометрии (авторы Бутузов, Кадомцев и др.), мы пришли к выводу, что там рассмотрены только эти три признака и еще четыре, относящиеся к равенству прямоугольных треугольников. Мы просмотрели учебно-методические комплекты других авторов. Но и в них для изучения предлагаются только три известные теоремы и четыре теоремы для прямоугольных треугольников.

Проблема: в школьном курсе геометрии изучается ограниченное количество признаков равенства треугольников, и почти нет задач на их практическое применение в деятельности человека.

Мы выдвинули гипотезу : есть ли еще какие-то признаки равенства треугольников, и можно ли применять на практике признаки равенства треугольников.

Для того чтобы убедиться, что данный вопрос интересен не только нам, мы провели анкетирование, результаты которого представлены в приложении 1. Наши предположения подтвердились, школьники действительно знают только признаки, которые изучает школьный курс геометрии, и о применении признаков в практической деятельности человека многие вообще не слышали.

Цель нашего исследования: найти дополнительные признаки равенства треугольников и показать применение признаков равенства треугольников в практической деятельности человека.

Изучить литературу по исследуемой теме;

Уточнить количество признаков равенства треугольников;

Проанализировать применение признаков равенства треугольников в практической деятельности человека;

Представить своим одноклассникам и обучающимся нашей школы все признаки равенства треугольников и применение некоторых из них в практической деятельности человека, оформив данные в виде брошюры.

Объект исследования: признаки равенства треугольников и их применение в практической деятельности человека.

Предмет исследования: треугольник, как основная фигура геометрии.

Метод исследования: теоретический (изучение, анализ, синтез), системно-поисковый, практический (доказательство теорем).

Видео:Признаки равенства треугольников. 7 класс.Скачать

Глава 1. Признаки равенства треугольников

Видео:Первый признак равенства треугольников. 7 класс.Скачать

Три основных признака равенства треугольников

Признаки равенства треугольников имели издавна важнейшее значение в геометрии, так как доказательство многочисленных теорем сводилось к доказательству равенства тех или иных треугольников. Доказательством признаков равенства треугольников занимались еще пифагорейцы. По словам Прокла, Евдем Родосский приписывает Фалесу Милетскому доказательство о равенстве двух треугольников, имеющих равными сторону и два прилежащих к ней угла (второй признак равенства треугольников).

Начнем с определения понятия равенства треугольников.

Треугольники АВС и А ₁ В ₁ С ₁ называются равными, если их можно совместить наложением.

Треугольник состоит из шести элементов: трех углов и трех сторон.

Тогда какое наименьшее количество элементов треугольника нужно взять для установления равенства двух треугольников?

Мы не сможем установить равенство двух треугольников по одному элементу, потому что неизвестно, будут ли равны остальные элементы.

Так же невозможно установить равенство двух треугольников, используя два элемента по причине нехватки информации для установления равенства.

Возможно установление равенства двух треугольников, используя три элемента. Но какие именно три элемента нужно назвать, для установления равенства треугольников?

При изучении этого вопроса, мы просмотрели школьные учебники геометрии различных авторов, а также словари и справочники, интернет ресурсы. В учебниках за седьмой класс предложены к изучению только три признака равенства треугольников.

Рассмотрим три основных признака равенства треугольников, изучаемых в школьном курсе геометрии.

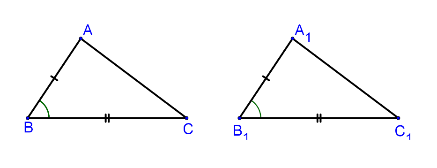
Первый признак: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Рис.1

Так как ∠ А = ∠ А ₁ , то треугольник ABC можно наложить на треугольник А ₁ В ₁ С ₁ так, что вершина А совместится с вершиной А ₁ , а стороны АВ и АС наложатся соответственно на лучи А ₁ В ₁ и A ₁ C ₁ . Поскольку АВ = A ₁ B ₁ , АС = А ₁ С ₁ , то сторона АВ совместится со стороной А ₁ В ₁ а сторона АС — со стороной А ₁ C ₁ ; в частности, совместятся точки В и В ₁ , С и C ₁ . Следовательно, совместятся стороны ВС и В ₁ С ₁ . Итак, треугольники ABC и А ₁ В ₁ С ₁ полностью совместятся, значит, они равны. [ 3]

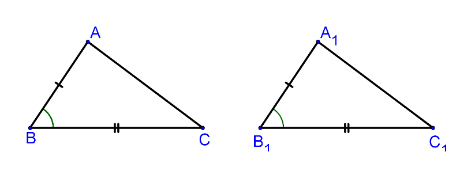
Признак второй: Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны .

Доказательство: Если в △ АВС и △ А ₁ В ₁ С ₁ будут иметь место следующие равенства AB=А ₁ В ₁ , ∠ BAC= ∠ B ₁ A ₁ C ₁ , ∠ АВС= ∠ А ₁ В ₁ С ₁ (рис. 2), наложим друг на друга треугольники А ₁ В ₁ С ₁ и АВС таким образом, чтобы совпали равные стороны AB и А ₁ В ₁ и углы, которые к ним прилегают. Как и в уже рассмотренном предыдущем примере, если это необходимо, треугольник А ₁ В ₁ С ₁ можно «перевернуть и приложить обратной стороной». Треугольники совпадут, следовательно, они могут считаться равными. Теорема доказана. [ 3] Рис. 2

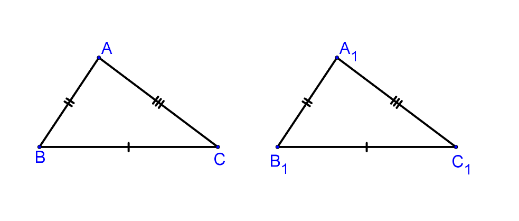
Признак третий: Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство: рассмотрим треугольники ABC и A ₁ B ₁ C ₁ , у которых AB = A ₁ B ₁ , BC = B ₁ C ₁ , CA = C ₁ A ₁ .Докажем, что треугольник ABC равен треугольнику A ₁ B ₁ C ₁ . Приложим треугольник ABC к треугольнику A ₁ B ₁ C ₁ так, чтобы вершина А совместилась с вершиной А ₁ , вершина В – с вершиной В ₁ , а вершины С и С ₁ оказались по разные стороны от прямой А ₁ В ₁ .

Возможны три случая: луч С ₁ С проходит внутри угла А ₁ С ₁ В ₁ ; луч С ₁ С совпадает с одной из сторон этого угла; С ₁ С проходит вне угла A ₁ B ₁ C ₁ (рис. 3). Рассмотрим первый случай (остальные случаи аналогичны).

Так как по условию теоремы стороны АС и А ₁ С ₁ , ВС и В ₁ С ₁ равны, то треугольники А ₁ С ₁ С и В ₁ С ₁ С – равнобедренные. По теореме о свойстве углов равнобедренного треугольника ∠ 1 = ∠ 2, ∠ 3= ∠ 4, поэтому ∠ A ₁ СВ ₁ = ∠ A ₁ B ₁ C ₁ . Итак, АС=А ₁ С ₁ , ВС = В ₁ С ₁ , ∠ C = C _1.

Следовательно, треугольник АВС равен треугольнику A ₁ B ₁ C ₁ равны по первому признаку равенства треугольников. Теорема доказана. [ 3] Рис.3

Из третьего признака равенства треугольников следует, что треугольник — жёсткая фигура. Представим себе две рейки, у которых два конца скреплены гвоздем. Такая конструкция не является жёсткой, однако, сдвигая или раздвигая свободные концы реек, мы можем менять угол между ними. Теперь возьмем ещё одну рейку и скрепим её концы со свободными концами первых двух реек. Полученная конструкция — треугольник — будет уже жёсткой. В ней нельзя сдвинуть или раздвинуть никакие две стороны, т. е. нельзя изменить ни один угол. Действительно, если бы это удалось, то мы получили бы новый треугольник, не равный исходному. Но это невозможно, так как новый треугольник должен быть равен исходному по третьему признаку равенства треугольников.

Итак, мы привели основные признаки равенства треугольников и доказали их. Также в школьном курсе геометрии изучаются признаки равенства прямоугольных треугольников. Рассмотрим их подробнее в следующем параграфе.

Видео:Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Признаки равенства прямоугольных треугольников

Так как в прямоугольном треугольнике угол между двумя катетами прямой, а любые два прямых угла равны, то из первого признака равенства треугольников следует:

Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны .

Далее, из второго признака равенства треугольников следует:

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.

Рассмотрим еще два признака равенства прямоугольных треугольников.

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.

Доказательство. Из свойства 1 (сумма двух острых углов прямоугольного треугольника равна 90 0 ) следует, что в таких треугольниках два других острых угла также равны, поэтому треугольники равны по второму признаку равенства треугольников, то есть по стороне (гипотенузе) и двум прилежащим к ней углам. Теорема доказана.

Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.

Доказательство. Рассмотрим треугольники АВС и А ₁ В ₁ С ₁ , у которых С и С ₁ -прямые, АВ=А ₁ В ₁ , ВС=В ₁ С ₁ . Докажем, АВС=А ₁ В ₁ С ₁ .

Так как С=С ₁ , то треугольник АВС можно наложить на треугольник А ₁ В ₁ С ₁ , так что вершина С совместиться с вершиной С ₁ , а стороны СА и СВ наложатся соответственно на учи С ₁ А ₁ и С ₁ В ₁ . Поскольку СВ=С ₁ В ₁ , то вершина В совместится с вершиной В ₁ . Но тогда вершины А и А ₁ также совместятся. В самом деле, если предположить, что точка А совместится с не которой другой точкой А ₂ луча С ₁ А ₁ , то получим равнобедренный треугольник А ₁ В ₁ С ₂ , в котором углы при основании А ₁ А ₂ не равны. Но это невозможно, поэтому вершины А и А1 совместятся. Следовательно, полностью совместятся треугольники АВС и А ₁ В ₁ С ₁ , т.е. они равны. Теорема доказана. [ 3]

Итак, мы рассмотрели еще 4 признака равенства треугольников. Данные признаки применимы только к прямоугольным треугольникам. В следующем параграфе представим еще несколько признаков равенства треугольников.

Видео:ТРИ ПРИЗНАКА РАВЕНСТВА ТРЕУГОЛЬНИКОВ НА ЕГЭ #shorts #математика #егэ #огэ #профильныйегэ #геометрияСкачать

Дополнительные признаки равенства треугольников

В справочнике по элементарной математике М. Я. Выгодского мы нашли еще один признак равенства треугольников.

1) Если две стороны и угол, лежащий против большей из них одного треугольника соответственно равны двум сторонам и углу, лежащему против большей из них другого треугольника, то такие треугольники равны.

Приведем доказательство данного признака.

Расположим треугольники так, как на рисунке 4. Соединим B и B ₁ , тогда ΔАВВ ₁ -равнобедренный, значит ∠ 1= ∠ 2. ∠ 3= ∠ 4 как остатки равных углов.

Получим ΔВСВ ₁ — равнобедренный, отсюда ВС=В ₁ С ₁ . ΔАВС = ΔА ₁ В ₁ С ₁ по трем сторонам. Теорема доказана. [ 1 ]

В формулировки признаков равенства треугольников можно включать не только стороны и углы, но и другие элементы треугольников. Рассмотрим несколько формулировок признаков равенства треугольников по трем элементам, включающим стороны, углы, высоты, биссектрисы и медианы треугольников. Выясним справедливость соответствующих признаков.

2) Если две стороны и высота, проведенная к одной из них, одного треугольника соответственно равны двум сторонам и высоте, проведенной к одной из них, другого треугольника, то такие треугольники равны. Дано: AB = A ₁ B ₁ , BC = B ₁ C ₁ , AK = A ₁ K ₁ ,

Доказательство: ΔABK=ΔA ₁ B ₁ K ₁ по гипотенузе и катету, тогда ∠ B= ∠ B ₁ и

получим ΔABC= ΔA ₁ B ₁ C ₁ по первому признаку. Теорема доказана. [7 ]

3) Если две стороны и медиана, проведенная к одной из них, одного треугольника соответственно равны двум сторонам и медиане, проведенной к одной из них, другого треугольника, то такие треугольники равны.

Доказательство: ΔABK=ΔA ₁ B ₁ K ₁ по трем

сторонам, значит ∠ B= ∠ B ₁ и ΔABC= ΔA ₁ B ₁ C ₁ по первому признаку. Теорема доказана. [7 ] Рис. 6

4) Если два угла и высота, проведенная из третьего угла, одного треугольника соответственно равны двум углам и высоте, проведенной из третьего угла, другого треугольника, то такие треугольники равны.

Доказательство: ΔABK=ΔA ₁ B ₁ K ₁ по катету

и острому углу, значит BK=B ₁ K ₁ , Рис. 7

ΔACK=ΔA ₁ C ₁ K ₁ по катету и острому углу, значит KC=K ₁ C ₁ , а, следовательно, BC=B ₁ C ₁ , а ΔABC= ΔA ₁ B ₁ C ₁ по второму признаку. Теорема доказана. [7 ]

5) Если сторона и две высоты, проведенные из углов, прилежащих к данной стороне, одного треугольника соответственно равны стороне и двум высотам, проведенным из углов, прилежащих к стороне, другого треугольника, то такие треугольники равны.

Доказательство: ΔAМC= ΔA ₁ М ₁ C ₁ по катету и гипотенузе, значит ∠ А = ∠ А ₁ , а ΔAКC= ΔA ₁ К ₁ C ₁ по катету и гипотенузе, значит

Итак, ΔABC= ΔA ₁ B ₁ C ₁ по второму признаку. Теорема доказана. [7 ]

6) Если две стороны и высота, проведенная к третьей стороне, одного треугольника соответственно равны двум сторонам и высоте, проведенной к третьей стороне, другого треугольника, то такие треугольники равны.

Доказательство: ΔABK=ΔA ₁ B ₁ K ₁ по гипотенузе и катету, значит AK=A ₁ K ₁ , ΔBКC= ΔB ₁ К ₁ C ₁ по катету и гипотенузе, значит KC=K ₁ C ₁ .

Итак, ΔABC= ΔA ₁ B ₁ C ₁ по трем сторонам. Теорема доказана. [7 ]

7) Если сторона, один из углов, прилежащих к этой стороне, и биссектриса этого угла одного треугольника соответственно равны стороне, одному из углов, прилежащих к этой стороне, и биссектрисе этого угла другого треугольника, то такие треугольники равны.

Доказательство: ΔКАС=ΔК ₁ А ₁ С ₁ по первому признаку, значит, ∠ С = ∠ С ₁ ,

ΔABC= ΔA ₁ B ₁ C ₁ по второму признаку. Теорема доказана. [7 ] Рис. 9

8) Если две высоты и угол, из которого проведена одна из высот, одного треугольника соответственно равны двум высотам и углу, из которого проведена одна из высот, другого треугольника, то такие треугольники равны.

Доказательство: ΔAМC= ΔA ₁ М ₁ C ₁ по катету и острому углу, ΔКАС=ΔК ₁ А ₁ С ₁ по катету и гипотенузе, ΔABC= ΔA ₁ B ₁ C ₁ по второму признаку. Теорема доказана. [7 ] Рис. 10

9) Если две стороны и медиана, проведенная к третьей стороне треугольника, соответственно равны двум сторонам и медиане, проведенной к третьей стороне другого треугольника, то такие треугольники равны.

Доказательство: пусть в треугольниках ABC и A ₁ B ₁ C ₁ AC = A ₁ C ₁ , BC = B ₁ C ₁ , медиана СM равна медиане С ₁ M ₁ . Докажем, что треугольники ABC и A ₁ B ₁ C ₁ равны. Продолжим медианы и отложим отрезки MD = CM и M ₁ D ₁ = C ₁ M ₁ . Четырехугольники ACBD и A ₁ С ₁ B ₁ D ₁ — параллелограммы. Треугольники ACD и A ₁ C ₁ D ₁ равны по трем сторонам. Следовательно, ACD = A ₁ C ₁ D ₁ . Аналогично, треугольники BCD и B ₁ C ₁ D ₁ равны по трем сторонам. Следовательно, Рис. 11

BCD = B ₁ C ₁ D ₁ . Значит, С = С ₁ и треугольники ABC и A ₁ B ₁ C ₁ равны по двум сторонам и углу между ними. Теорема доказана. [9]

10) Если два угла и высота, проведенная к стороне, к которой прилегают эти углы, одного треугольника, соответственно равны двум углам и высоте, проведенной к стороне, к которой прилегают эти углы, другого треугольника, то такие треугольники равны. [2]

11) Если сторона, высота и медиана, проведенные к стороне одного треугольника, соответственно равны стороне, высоте и медиане, проведенным к этой стороне другого треугольника, то эти треугольники равны.

Доказательство. Пусть в треугольниках ABC и A ₁ B ₁ C ₁ AC = A ₁ C ₁ , медианы CM и C ₁ M ₁ равны, высоты CH и C ₁ H ₁ равны. Докажем, что треугольники ABC и A ₁ B ₁ C ₁ равны. Действительно, прямоугольные треугольники ACH и A ₁ C ₁ H ₁ равны по гипотенузе и катету. Следовательно, A = A ₁ и AH = A ₁ H ₁ . Прямоугольные треугольники CMH и C ₁ M ₁ H ₁ равны по гипотенузе и катету. Следовательно, MH = M ₁ H ₁ , откуда AM = A ₁ M ₁ , значит, AB = A ₁ B ₁ . Таким образом, Рис. 12

треугольники ABC и A ₁ B ₁ C ₁ равны по двум сторонам и углу между ними. Теорема доказана. [9]

12) Если медиана и углы, на которые она делит угол, одного треугольника, соответственно равны медиане и углам, на которые она делит угол, другого треугольника, то эти треугольники равны. [2 ]

13) Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника, то такие треугольники равны.

Доказательство. Пусть в треугольниках ABC и A ₁ B ₁ C ₁ AB = A ₁ B ₁ , медиана AM равна медиане A ₁ M ₁ , медиана BK равна медиане B ₁ K ₁ . Докажем, что треугольники ABC и A ₁ B ₁ C ₁ равны. Точки O и O ₁ пересечения медиан Рис. 13

данных треугольников делят медианы в отношении 2:1, считая от вершины. Значит, треугольники ABO и A ₁ B ₁ O ₁ равны по трем сторонам. Следовательно,

BAO = B ₁ A ₁ O ₁ , значит, треугольники ABM и A ₁ B ₁ M ₁ равны по двум сторонам и углу между ними. Поэтому ABC = A ₁ B ₁ C ₁ . Аналогично доказывается, что

BAC = B ₁ A ₁ C ₁ . Таким образом, треугольники ABC и A ₁ B ₁ C ₁ равны по стороне и двум прилежащим к ней углам. Теорема доказана. [9 ]

14) Ели две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника, то такие треугольники равны.

Доказательство. Пусть в треугольниках ABC и A ₁ B ₁ C ₁ AC = A ₁ C ₁ , BC = B ₁ C ₁ , биссектриса CD равна биссектрисе С ₁ D ₁ . Докажем, что треугольники ABC и A ₁ B ₁ C ₁ равны. Продолжим стороны AC и A ₁ C ₁ и отложим на их продолжениях отрезки CE = BC и C ₁ E ₁ = B ₁ C ₁ . Тогда Треугольники BCE и B ₁ C ₁ E ₁ равны по трем сторонам. Значит, E = E ₁ и BE = B ₁ E ₁ . Треугольники ABE и A ₁ B ₁ E ₁ равны по двум сторонам и углу между Рис. 14

ними. Значит, AB = A ₁ B ₁ . Таким образом, треугольники ABC и A ₁ B ₁ C ₁ равны по трем сторонам. Теорема доказана. [9 ]

15) Два треугольника равны, если три медианы одного треугольника соответственно равны трем медианам другого треугольника.

Доказательство. Пусть в треугольниках ABC и A ₁ B ₁ C ₁ соответственно равны медианы AK и A ₁ K ₁ , BL и B ₁ L ₁ , CM и C ₁ M ₁ . Докажем, что треугольники ABC и A ₁ B ₁ C ₁ равны. Пусть O и O ₁ — Рис. 15

точки пересечения медиан данных треугольников. Заметим, что медианы OM и O ₁ M ₁ треугольников ABO и A ₁ B ₁ O ₁ равны, так как они составляют одну третью часть соответствующих медиан данных треугольников. По признаку равенства треугольников, доказанному нами под номером 13, треугольники ABO и A ₁ B ₁ O ₁ равны, значит, AB = A ₁ B ₁ . Аналогично доказывается, что BC = B ₁ C ₁ и AC = A ₁ C ₁ . Таким образом, треугольники ABC и A ₁ B ₁ C ₁ равны по трем сторонам. Теорема доказана. [9 ]

16) Два треугольника равны, если три высоты одного треугольника соответственно равны трем высотам другого треугольника.

Доказательство. Пусть в треугольниках ABC и A ₁ B ₁ C ₁ соответственно равны высоты AH и A ₁ H ₁ , BG и B ₁ G ₁ , CF и C ₁ F ₁ . Докажем, что треугольники ABC и A ₁ B ₁ C ₁ равны. Рис. 16

Обозначим стороны треугольников соответственно a , b , c и a ₁ , b ₁ , c ₁ , а соответствующие высоты h _a , b _b , h _c и h _{1 a} , h _{1 b} , h _{1 c} . Имеют место равенства ah _a = bh _b = ch _c и a ₁ h _{1 a} = b ₁ h _{1 b} = c ₁ h _{1 c} . Разделив почленно первые равенства на вторые, получим равенства из которых следует, что треугольники ABC и A ₁ B ₁ C ₁ подобны. Так как соответствующие высоты этих треугольников равны, то они не только подобны, но и равны. [9 ]

Мы рассмотрели дополнительные признаки равенства треугольников, доказательство каждого из них, в конечном счете, сводится к трем основным признакам равенства треугольников, изучаемых в школьном курсе геометрии.

Видео:Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать

Вывод по первой главе

В первой главе нами рассмотрены три основных признака равенства треугольников, признаки равенства прямоугольных треугольников и найдены дополнительные признаки равенства треугольников. Всего в нашей работе отражено 3 основных признака равенства треугольников, 4 признака равенства прямоугольных треугольников и 16 дополнительных признаков равенства треугольников. Мы представили доказательство каждого признака и заметили, что признаки доказываются либо способом наложения, либо сводятся к одному из трех основных признаков равенства треугольников.

Видео:Признаки равенства треугольников. Практическая часть. 7 класс.Скачать

Глава 2. Применение признаков равенства треугольников в практической деятельности человека.

В глубокой древности вместе с астрономией появилась наука – тригонометрия. Слово «тригонометрия» произведено от греческих «треугольник» и «меряю». Буквальное значение – «наука об измерении треугольников».

С помощью натянутых веревок длиной 3, 4 и 5 единиц египетские жрецы получали прямые углы при возведении храмов и т.п.

Искусство изображать предметы на плоскости с Древних времён привлекает к себе внимание человека, люди рисовали на скалах, стенах, сосудах и прочих предметах быта, различные орнаменты, растения, животных. Люди стремились к тому, чтобы изображение правильно отображало естественную форму предмета.

Мы во второй главе рассмотрим, как можно применять признаки равенства треугольников в практической деятельности человека.

Теорему о равенстве треугольников по двум сторонам и углу между ними Фалес использовал для определения расстояния от берега до морских кораблей. [ 10 ]

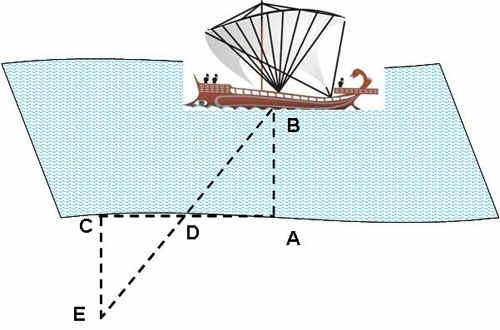
Каким способом пользовался при этом Фалес, точно не известно. Предполагают, что один его способ состоял в следующем: пусть A – точка берега, B – корабль на море. Для определения расстояния AB восстанавливают на берегу перпендикуляр произвольной длины AC к AB; в противоположном направлении восстанавливают CE к AC так, чтобы точки D (середина AC), B и E находились на одной прямой. Тогда CE будет равна искомому расстоянию AB. Доказательство основывается на втором признаке равенства треугольников Рис. 17

(DC = DA; С = A; EDС = BDA как вертикальные).

Предполагают второй способ, которым древнегреческий математик Фалес первым решил задачу о вычислении расстояния от берега до корабля. Для этого он измерил расстояние АВ и угол ABC . Затем, произведя на суше некоторые построения и измерения, он вычислил расстояние АС.

Построить АВН = ABC , а также построить АЕ перпендикулярно АВ. Точка пересечения лучей ВН и АЕ — вершина треугольника АВМ, равного треугольнику ABC .

Треугольник ABC равен треугольнику АВМ по второму признаку равенства треугольников, значит, у этих треугольников соответствующие стороны равны, т. е. АС = AM , для нахождения расстояния АС от берега до корабля достаточно измерить расстояние AM на местности.

У нас возник вопрос, а каким способом, с помощью какого инструмента можно построить на местности АС перпендикулярно АВ.

Мы выяснили, что для этой цели можно воспользоваться измерительными инструментами экер и теодолит.

Экер (франц. équerre, от позднелат. exquadro — нарезаю четырёхугольник), простейший геодезический инструмент, служащий для построения на местности углов, кратных 90° или 45°.

Теодоли́т — измерительный прибор для определения горизонтальных и вертикальных углов при топографических съёмках , геодезических и маркшейдерских работах, в строительстве и т. п.

Маркшейдерские работы – это работы, которые проводятся для изучения процессов деформации горных пород и земной поверхности в связи с горными работами.

Угол ABC на местности можно измерить с помощью астролябии.

Астролябия (греч. ἁστρολάβον , астролабон , «берущий звезды») — прибор для определения широты, один из старейших астрономических инструментов. Основан на принципе стереографической проекции.

А вот как в Древнем Египте применили первый признак равенства треугольников (по двум сторонам и углу между ними). Автором также считается Фалес Милетский, для измерения высоты пирамиды: представим, что мы стоим перед огромной пирамидой, как же измерить её высоту? Ведь к ней не приложишь измерительные приборы! И тут на помощь Фалесу Милетскому приходит первый признак равенства треугольников: он подождал пока тень его точно совпадёт с его ростом, применил теорему, получилось, что высота пирамиды равна её тени (рис. 18). Рис. 18

Мы взяли практическую задачу на вычисление ширины озера .

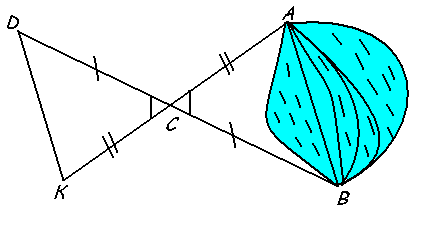
Для определения ширины озера на его берегу отметили точки А и В, а потом еще точки С, D и О так, что точка О – общая середина отрезков АС и BD . Измерив CD , определим ширину озера.

Но для такого способа нужно много Рис. 19

свободного пространства, чтобы сделать эти измерения. [ 5 ]

Приведем еще один похожий пример.

На рисунке показан способ измерения расстояния от А до В по озеру . Известно, что ОС=ОD, ОВ=ОЕ. Докажите, что АВ=ЕF.

Вот еще несколько практических задач, при решении которых необходимо использовать признаки равенства треугольников.

5) Чтобы измерить на местности расстояние между двумя точками А и В, из которых одна (точка А) недоступна , провешивают направление отрезка АВ (рис. 21 ) и на его продолжении отмеряют произвольный отрезок ВЕ. Выбирают на местности точку D , из которой видна точка А и можно пройти к точкам В и Е. Провешивают прямые BDQ и EDF и отмеряют FD = DE и DQ = BD . Затем идут по прямой FQ , глядя на точку А, пока не найдут точку Н, которая лежит на прямой AD . Тогда HQ равно искомому расстоянию. [ 4 ] Рис. 21

6) Мама купила 1м ткани шириной 1м на платки двум дочерям. Разделите этот кусок ткани на две равные части; докажите правильность своих действий. (Сгибаем ткань по диагонали; полученные треугольники равны по 3 признаку равенства треугольников). [ 8 ]

7) Два дома одинаково удалены от берега реки. Где нужно сделать причал для лодок, чтоб он был одинаково удален от обоих домов?

, АН=НВ, НС, НС – серединный перпендикуляр. [8]

Мы рассмотрели 7 практических задач на применение признаков равенства треугольников. Признаки равенства треугольников издавна применялись человечеством для решения задач, связанных с практической деятельностью человека. Все данные задачи сводятся к задаче на вычисление расстояния до недоступной точки (расстояние до кораблей, расстояние до острова на озере и тому подобное), и вычисление ширины объекта (ширина озера), и также вычисление высоты предмета (вычисление высоты пирамиды).

Видео:7 класс, 19 урок, Второй признак равенства треугольниковСкачать

Вывод по второй главе

Во второй главе мы рассмотрели практическое применение признаков равенства треугольников в деятельности человека. Признаки применялись на практике с древних времен. Сегодня мы можем использовать признаки также при решении практических задач. Все представленные задачи мы нашли в литературе и на интернет ресурсах.

Видео:Геометрия. 7 класс. Теоремы. Т3. Первый признак равенства треугольников.Скачать

Заключение

Выдвинутая нами гипотеза подтвердилась, мы действительно нашли признаки равенства треугольников, отличительные от трех основных, представленных в школьном курсе геометрии.

В своей работе нами проведено исследование данного вопроса в виде анкетирования, который показал, что обучающиеся в основной массе не знают другие признаки и их применение в практической деятельности человека, а также изучили литературу и многие интернет ресурсы, выделили и доказали другие признаки треугольников. Сейчас мы знаем 3 основных признака равенства треугольников, 4 признака равенства прямоугольных треугольников и 16 дополнительных признаков равенства треугольников. Мы представили доказательство многих признаков и заметили, что признаки доказываются либо способом наложения, либо сводятся к одному из трех основных признаков равенства треугольников.

Нами изучено и практическое применение некоторых признаков равенства треугольников, приведены практические задачи, которые решались с помощью применения признаков равенства треугольников. Мы уверены, что спектр применения признаков равенства треугольников гораздо шире, чем тот, что привели в своей работе мы, но на данном этапе, мы считаем, что выполнили все поставленные нами задачи и доказали гипотезу.

Итак, признаков действительно больше, чем показано в школьных учебниках, и признаки применимы в практической деятельности человека.

Видео:Первый признак равенства треугольников | Теорема + доказательствоСкачать

Список литературы

Выгодский М. Я. Справочник по элементарной математике: таблицы, арифметика, алгебра, геометрия, тригонометрия, функции и графики. — Переиздание. — М.: АСТ, 2006, — 509 с.

Геометрия в схемах, терминах, таблицах / А.Н. Роганин. – Изд. 5-е. – Ростов н/Д: Феникс, 2016. – 96 с.

Геометрия. 7-9 классы: учеб. для общеобразоват. организаций / [Л.С.Атанасян, В.Ф.Бутузов, С.Б. Кадомцев и др.] – 8-е изд. – М.: Просвещение, 2018. – 383 с.

Геометрия. 7-9 классы: учеб. для общеобразоват. организаций / А.В. Погорелов. – 2-е изд. – М.: Просвещение, 2014. – 240 с.

Геометрия: 7 класс: учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В. Б. Полонский, М. С. Якир. – М.: Вентана-Граф, 2015. – 192 с.

Глейзер Г. И. История математики в школе. VII-VIII классы. Пособие для учителей. — М.: Просвещение, 1982. — С. 76—95. — 240 с.

Инфоурок URL: https://infourok.ru/issledovatelskaya-rabota-po-matematike-uchenici-a-klassa-nestandartnie-priznaki-ravenstva-treugolnikov-3351282.html (дата обращения: 12.12.2019 г.).

Крымова Л. Применение признаков равенства треугольников к решению практических задач. 7 класс // Математика. — 2004. — № 19.

Смирнов В., Смирнова И. Признаки равенства треугольников // Математика. — 2009. — № 22.

Треугольник // Википедия. Свободная энциклопедия URL: https://ru.wikipedia.org/wiki/ (дата обращения: 15 января 2020).

Энциклопедия для детей. Т. 11. Математика / Глав. ред. М. Д. Аксёнова: метод. и отв. ред. В. А. Володин. – М.: Аванта+, 2003. – 688 с.

Видео:Геометрия 7 класс (Урок№14 - Второй и третий признаки равенства треугольников.)Скачать

Приложение 1

Результаты анкетирования « Признаки равенства треугольников и их применение в практической деятельности человека».

Сколько признаков равенства треугольников вы знаете?

Хотели бы вы узнать еще несколько признаков равенства треугольников? Можно ли применять признаки равенства треугольников в практической деятельности человека?

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Исследовательский проект «Применение равенства треугольников при измерительных работах»

Просмотр содержимого документа
«Исследовательский проект «Применение равенства треугольников при измерительных работах»»

Муниципальное общеобразовательное учреждение

«Санаторная школа-интернат №2 для детей, нуждающихся в длительном лечении»

«Применение равенства треугольников при измерительных работах»

Автор проекта: обучающаяся 7 «Б» класса Душутина Маргарита

Наставник проекта: учитель математики Анненкова Татьяна Николаевна

ГЛАВА 1 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПО ТЕМЕ «ПРИМЕНЕНИЕ ПОДОБИЯ ТРЕУГОЛЬНИКОВ ПРИ ИЗМЕРИТЕЛЬНЫХ РАБОТАХ» 6

1.1 Историческая справка о признаках равенства треугольника 6

1.2 Признаки равенства треугольников. Жесткий треугольник 8

ГЛАВА 2 ПРАКТИЧЕСКАЯ ЧАСТЬ ПО ТЕМЕ «ПРИМЕНЕНИЕ РАВЕНСТВА ТРЕУГОЛЬНИКОВ ПРИ ИЗМЕРИТЕЛЬНЫХ РАБОТАХ» 9

2.1 Практические задачи по теме «Применение равенства треугольников при измерительных работах» 9

2.2 Задача на измерение расстояния между двумя недосягаемыми объектами 11

Список литературы 14

Геометрию можно считать одной из самых древних наук. Наука в начале своего развития для человека несла практическую деятельность. Только лишь потом она сформировалась как самостоятельная наука, которая изучает геометрические фигуры. Геометрические знания активно применяются у людей в жизни, в науки, в быту, на производстве. Мы должны уметь рассчитать количество обоев в комнату, посчитать площадь квартиры и др. Кто-то с лёгкостью выполняет геометрические построения при изготовлении технических чертежей, или определяет расстояние до предмета. Геометрия всегда помогала решить те задачи, перед которыми её ставила жизнь[7].

Треугольник является центральной фигурой всей геометрии. При решении задач используют его самые разнообразные свойства. Свойства треугольника широко применяют на практике. Например, в архитектуре; при разработке чертежа здания, при планировке будущих квартир; в промышленности: при проектировании различны деталей, при изготовлении стройматериалов, при строительстве морских и авиа судов; в навигации: для проложения правильного и максимально точного маршрута; в астрологии и астрономии, одним словом просто необходимо знать треугольник и все его свойства. Одно из важнейших свойств для пары треугольников, устанавливать их равенство. Существует ряд задач на тему установления равенства двух треугольников. Основная фигура, которую изучают в геометрии 7 класса – это треугольник. Познакомившись с признаками равенства треугольников, мы узнали и о таком понятии как жесткость треугольника. Учитель на уроке часто рассказывает о практической направленности математики, знакомит с историческим материалом. Мы решили подготовить учебный проект по теме: «Признаки равенства треугольников в измерительных работах».

Геометрия помогает человеку идти по миру с широко открытыми глазами, учит внимательно смотреть вокруг и видеть красоту обычных вещей, смотреть и думать, думать и делать выводы.

Объект: изучение признаков равенства треугольников

Цель: Изучение применения равенства треугольников при измерительной работе на местности.

Проанализировать проблему исследования.

Исследовать исторические факты по проблеме исследования

Рассмотреть признаки равенства треугольников

Подобрать различные задачи на использование равенства треугольников

Научиться применять признаки равенства треугольников при решении геометрических задач на местности

Выполнить практическую работу

Гипотеза: если использовать признак равенства треугольников, то можно измерить расстояние между двумя не досягаемыми объектами.

ГЛАВА 1 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПО ТЕМЕ «ПРИМЕНЕНИЕ ПОДОБИЯ ТРЕУГОЛЬНИКОВ ПРИ ИЗМЕРИТЕЛЬНЫХ РАБОТАХ»

1. Историческая справка о признаках равенства треугольника

Признаки равенства треугольников имели издавна важнейшее значение в геометрии, так как доказательства многочисленных теорем сводилось к доказательству равенства тех или иных треугольников. Доказательством признаков равенства треугольников занимались еще пифагорейцы. По словам Прокла, Евдем Родосский приписывает Фалесу Милетскому доказательство о равенстве двух треугольников, имеющих равными сторону и два прилежащих к ней угла (второй признак равенства треугольников).

Эту теорему Фалес использовал для определения расстояния от берега до морских кораблей. Каким способом пользовался при этом Фалес, точно не известно. Предполагают, что один его способ состоял в следующем: пусть A – точка берега, B – корабль на море. Для определения расстояния AB восстанавливают на берегу перпендикуляр произвольной длины AC к AB; в противоположном направлении восстанавливают CE к AC так, чтобы точки D (середина AC), B и E находились на одной прямой. Тогда CE будет равна искомому расстоянию AB. Доказательство основывается на втором признаке равенства треугольников (DC = DA; С = A; EDС = BDA как вертикальные).

Рис. 1.1 Макет задачи по определению расстояния от берега до морских кораблей

Предполагают второй способ, которым древнегреческий математик Фалес первым решил задачу о вычислении расстояния от берега до корабля. Для этого он измерил расстояние АВ и угол ABC. Затем, произведя на суше некоторые построения и измерения, он вычислил расстояние АС.

Построить АВН = ABC, а также построить АЕ перпендикулярно АВ. Точка пересечения лучей ВН и АЕ — вершина треугольника АВМ, равного треугольнику ABC.

Треугольник ABC равен треугольнику АВМ по второму признаку равенства треугольников, значит, у этих треугольников соответствующие стороны равны, т. е. АС = AM, для нахождения расстояния АС от берега до корабля достаточно измерить расстояние AM на местности при помощи теодолита или астралябии.

Теодоли́т — измерительный прибор для определения горизонтальных и вертикальных углов при топографических съёмках, геодезических и маркшейдерских работах, в строительстве и т. п.

Маркшейдерские работы — это работы, которые проводятся для изучения процессов деформации горных пород и земной поверхности в связи с горными работами

Рис. 1.2 Теодолит

Угол ABC на местности можно измерить с помощью астролябии.

Астролябия (греч. ἁστρολάβον, астролабон, «берущий звезды») — прибор для определения широты, один из старейших астрономических инструментов. Основан на принципе стереографической проекции.

Рис. 1.3 Астролябия

А вот как в Древнем Египте применили первый признак равенства треугольников (по двум сторонам и углу между ними), создателем его также считается Фалес Милетский, для измерения высоты пирамиды: представим, что мы стоим перед огромной пирамидой, как же измерить её высоту? Ведь к ней не приложишь измерительные приборы! И тут на помощь Фалесу Милетскому приходит первый признак равенства треугольников: он подождал пока тень его точно совпадёт с его ростом, применил теорему, получилось, что высота пирамиды равна её тени (рис. 2).

Рис. 1.4 Фалес Милетский измеряет высоту пирамиды

1. Признаки равенства треугольников. Жесткий треугольник

Первый признак: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Рис. 1.5 Первый признак равенства треугольников

Второй признак: Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Рис. 1.6 Второй признак равенства треугольников

Третий признак: Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.

Рис. 1.7 Третий признак равенства треугольников

Из третьего признака равенства треугольников следует, что треугольник — жёсткая фигура. Потому, что: можно представим себе две рейки, (рис 1) у которых два конца скреплены гвоздем. Такая конструкция не является жёсткой однако сдвигая или раздвигая свободные концы реек, мы можем менять угол между ними. Теперь возьмем ещё одну рейку и скрепим её концы со свободными концами первых двух реек.(рис 2) Полученная конструкция — треугольник — будет уже жёсткой. В ней нельзя сдвинуть или раздвинуть никакие две стороны, т. е. нельзя изменить ни один угол. Действительно, если бы это удалось, то мы получили бы новый треугольник, не равный исходному. Но это невозможно, так как новый треугольник должен быть равен исходному по третьему признаку равенства треугольников.

Если жесткий треугольник мы решим увеличить или уменьшить в несколько раз, то увеличится или уменьшится в это число раз каждая его сторона, и тем самым п 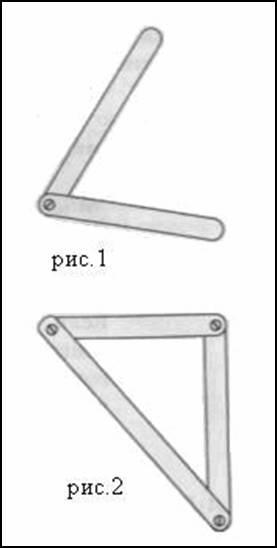олучим третий признак равенства треугольников.

Это свойство – жесткость треугольника – широко используется на практике. Так, чтобы закрепить столб в вертикальном положении, к нему ставят подпорку; такой же принцип используется при установке кронштейна.

Свойство жесткости треугольника широко используют в практике при строительстве железных конструкций.

Рис. 1.8 Модель жесткого треугольника

ГЛАВА 2 ПРАКТИЧЕСКАЯ ЧАСТЬ ПО ТЕМЕ «ПРИМЕНЕНИЕ РАВЕНСТВА ТРЕУГОЛЬНИКОВ ПРИ ИЗМЕРИТЕЛЬНЫХ РАБОТАХ» 2.1 Практические задачи по теме «Применение равенства треугольников при измерительных работах»

Задача1. Бригада по прокладке дорог должна сделать тоннель, но расстояние, которое нужно пробить через гору, не известно. Что должна предпринять бригада, чтобы узнать это расстояние, если известно расстояние от А до С и от В до С (рис. 1)?

Рис. 2.1 Эскиз к задаче 1

Бригада не может проложить дорогу вокруг горы. Поэтому они предприняли небольшую хитрость: на месте входа в еще не прорубленный тоннель поставили человека – (А) и на месте выхода тоже – (В), сбоку горы поставили третьего человека – (С), образовался треугольник ABC. Человек А прокладывает прямую через точку С, и человек В тоже прокладывает прямую через точку С. Проведя прямые и поставив на них на определенном расстоянии еще двух людей – (D, E) так, что CD = AC, а СВ = ЕС. Угол ACB = ECD по свойству вертикальных углов, поэтому треугольник DEC равен треугольнику ABC. Теперь бригада соединяет отрезком на местности точки D и Е. Рабочим остается измерить расстояние от Е до D, которое будет равно искомому расстоянию от А до В.

Задача 2. Мама купила 1,2м ткани шириной 1,2м для дочерей на выступление. Её надо из этого куска ткани сделать два одинаковых платка. Как разделить поровну?

Сгибаем ткань по диагонали; полученные треугольники равны по третьему признаку равенства треугольников.

На примере бумажного листа докажем это решение.

Задача 3. Вычислить длину озера.

При измерении длины озера отметили на местности точки А, В и С, а затем еще две точки D и К, так, чтобы точка С оказалась серединой отрезков АК и ВD. Измерив DК, получили 500 м и сделали вывод, что длина озера равна 500м.

Рис. 2.2 Эскиз к задаче 3

2.2 Задача на измерение расстояния между двумя недосягаемыми объектами

Для эксперимента мы решили взять за основу задачу для нахождения расстояния между двумя недосягаемыми объектами. Но для такого способа нужно много свободного пространства, чтобы сделать эти измерения.

Рис. 2.3 Место эксперимента

Задача: Вычислить расстояние для асфальтирования дорожки в квартале

Проблема в том, что местность очень неровная и на пути лежат препятствия.

Чтобы решить поставленную перед нами задачу мы взяли рулетку, относительно толстую нить, и 5 колышков. Пошли к месту измерения. Два колышка крепко вставили в землю там, где начало и конец будущей дорожки. На схеме это точки А и В. Третий кол мы поставили в удобное для нас место и назвали эту точку С. Договоримся далее наши колышки называть точками. Далее нитью соединили точки А и С, а также точки В и С. Мы получили отрезки АС и ВС. При помощи рулетки узнаем, чему равны эти отрезки.

Рис. 2.4 Метки на местности

АС =51 м; ВС = 37,5 м

На продолжении стороны АС продолжаю отматывать нить до тех пор, пока наше расстояние будет равно отрезку АС. Далее на это место вставляю колышек и обозначу его точкой М, имеем АС=СМ. Аналогично, на продолжении ВС равный ему отрезок ВК, т. е. ВС=СК. Важно учитывать равенство угла АСВ и угла МСК. Соединим нитью точки КМ. Т. к.

В результате проведенной работы мы проанализировали литературу разных авторов по проблеме исследования. Повторили признаки равенства треугольников и разобрала решения задач различного уровня сложности, решаемые с применением признаков равенства треугольников. Эта информация поможет мне при подготовке к экзаменам. Подробно разбирая разные задачи на измерение расстояния между недосягаемыми объектами, мы научились видеть равные треугольники в различных ситуациях. Мы умеем правильно записывать соответственно равные стороны и углы, по известным элементам, вычислять неизвестные стороны, используя признаки равенства треугольников.

Нами было выяснено на конкретных примерах, что с помощью признаков равенства треугольников можно измерить расстояние между двумя не досягаемыми объектами. Мы научились применять признаки равенства треугольников для решения практических задач.

На наш взгляд проведённая работа практически значима, подобранный и разработанный материал может быть использовано как учениками, так и учителями, работающими в-седьмых классах, по ранее обозначенной теме.

На основе практической работы был сделан вывод об истинности выдвинутой гипотезы.

Атанасян Л.С., Бутузов В.Ф. Геометрия 7-9 класс. Москва: Просвещение, 2010. 384 с.

Болтянский В.Г. Элементарная геометрия. Москва: Просвещение, 1985 . 325 с.

Ганьшин В.Н. Простейшие измерения на местности.- 3-е изд. М.: Недра, 1983. – 112 с. [Электронный ресурс]. URL: http://libhist.narod.ru/Prosteishie_izmer_Ganshin.pdf (дата обращения 12.12.2017).

Глейзер Г.И. История математики в школе. Москва: Просвещение, 1982. 240 с.

Мерзляк А. Г., Полонский В. Б. Геометрия 7 класс. М: Дрофа, 2016. 193 с.

Мерзляк А. Г., Полонский В. Б. Геометрия 8 класс. М: Вентана-Граф, 2017. 208 с.

Ширина И. М. Практическое применение треугольников при измерительных работах. – Пермь, 2016. [Электронный ресурс]. URL: http://genius.pstu.ru/file.php/1/pupils_works_2016/Shirinkina.pdf (дата обращения 5.11.2017)

Энциклопедический словарь юного математика. Москва: Педагогика, 1983. 351 с.

Видео:Признаки Равенства Треугольников, для Чайников, Геометрия 7 класс, 3-й Урок:Скачать

Обобщающий урок геометрии по теме «Решение задач на применение признаков равенства треугольников». 7-й класс

Разделы: Математика

Класс: 7

Дидактическая задача урока: систематизировать знания и умения учащихся решать задачи на применение признаков равенства треугольников, уметь делать обобщение изучаемых фактов.

Цели:

Образовательные:

• Повторить и закрепить знание учащимися формулировок признаков равенства треугольников.
• Формирование умений:
  • распознавать равные треугольники;
  • доказывать их равенство;
  • делать выводы о равенстве некоторых их элементов.
• Тренировать способность решать задачи, используя признаки равенства треугольников

Воспитательные:

• Воспитывать аккуратность и прилежание.
• Прививать положительное отношение к знаниям, к процессу учения.
• Формировать самостоятельность и умение делать самооценку.

Развивающие:

• Развивать творческие способности, познавательную активность.
• Развивать умение решать задачи по готовым чертежам, развивать логическое мышление.
• Учить разрешению проблемы, частично-поисковой деятельности учащихся.
• Развивать внимание, слуховую и зрительную память.
• Формировать математическую речь учащихся.

Тип урока: урок систематизации и обобщения знаний, умений, навыков.

Методическое обеспечение урока:

• Компьютер.
• Мультимедиа-проектор.
• Листы с печатной основой – карточки с тестами на знание признаков равенства треугольников, карточки с заданиями для работы на уроке.
• Презентация.

Ход урока

1. Организационный момент.

Проверка готовности учащихся к уроку. Эмоциональный настрой учащихся.

2. Актуализация знаний.

Фронтальная работа с классом.

— Какую геометрическую фигуру изучаем? (Треугольник).

— Проверим, что вы уже знаете об этой фигуре.

— Какие вы знаете виды треугольников? (Остроугольный, прямоугольный, тупоугольный, равнобедренный и равносторонний)

— Какие треугольники называются равными? (Которые можно совместить при наложении)

— Что помогает определить равенство треугольников? (Признаки равенства треугольников)

— Какие признаки равенства треугольников вы знаете? Посмотрите на экран.

— Какой признак равенства треугольников вы здесь видите?

— Какой признак равенства треугольников вы видите здесь?

— Какой признак равенства треугольников вы здесь видите?

Выполнение теста «Верно-неверно».

На столах у каждого из вас лежат опросные листы. Мы будем работать с ними на протяжении всего урока. Выполним следующее задание №1. Если вы согласны с утверждением ставите +, если нет, ставите –.

Учащимся дается время (3 мин.) на выполнение задания.

Слайды 5-6.

Утверждение

Если в треугольнике две стороны равны, то треугольник называется равнобедренным.

Отрезок, соединяющий вершину треугольника с противоположной стороной, называется медианой треугольника.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Если сторона и два угла одного треугольника равны соответственно стороне и двум углам другого треугольника, то такие треугольники равны.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

В треугольнике углы при основании равны.

Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой.

Если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники равны.

После учитель вместе с учащимися осуществляет проверку, используя проектор.

1. Если в треугольнике две стороны равны, то треугольник называется равнобедренным. (+)

2. Отрезок, соединяющий вершину треугольника с противоположной стороной, называется медианой треугольника. (–) (пропущено слово: середина).

3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. (+)

4. Если сторона и два угла одного треугольника равны соответственно стороне и двум углам другого треугольника, то такие треугольники равны. (–) (Правильно: два угла, прилежащих к ней).

5. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. (+)

6. В треугольнике углы при основании равны. (–) (Пропущено слово: равностороннем или равнобедренном).

7. Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой. (+)

8. Если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники равны. (–)

— Переведите полученные баллы в отметку (на листах контроля сказано, как это сделать).

• 8 баллов – отметка «5»
• 7-6 баллов – отметка «4»
• 5-4 баллов – отметка «3»
• Менее 4 баллов – «будем работать дальше»

Поставьте полученную отметку в лист контроля.

— Поднимите руки те, кто получил – 5, кто получил – 4, кто получил – 3. С остальными будем работать дальше.

3. Формулировка темы и целей урока.

— Ребята, первый год вы изучаете предмет геометрия и поняли, что предметом изучения этого раздела математики является решение задач на основе изученных определений, свойств и теорем. Но чтобы хорошо научиться решать задачи, что для этого выполнять? (Дети отвечают).

— А ещё известный педагог и математик Дъёрдь Пойа (1887-1985) сравнивал умение решать задачи с умением научиться плавать.

Если вы хотите научиться плавать, то смело входите в воду,
а если хотите научиться решать задачи, то решайте их. (Д.Пойа)

Дъёрдь Пойа, венгерский, швейцарский и американский математик, много работал со школьными учителями математики и внёс большой вклад в популяризацию науки. Он написал несколько книг о том, как решают задачи и как надо учить решать задачи.

— Сформулируйте цели урока. Чем мы будем заниматься и чего должны достичь к концу урока? (Учащиеся формулируют цели – Решение задач на применение признаков равенства треугольников) Слайд 9.

4. Решение задач.

— В геометрии очень важно уметь смотреть и видеть, замечать и отмечать различные особенности геометрических фигур.

«Если знаешь — докажи». Выполнение задания по готовым чертежам (устная работа с классом).

Следующее задание. Ваша задача по готовому чертежу доказать равенство треугольников.

Слайд 10. №1

Слайд 11. №2

Слайд 12. №3.

Слайд 13. №4.

5. Историческая справка о признаках равенства треугольников.

— Ребята! Сейчас в своей работе вы использовали такой приём, как доказательство. Эта форма работы вам уже известна. А до VI века с доказательством люди вообще были не знакомы. Первым учёным, который стал рассуждать, доказывать, был Фалес Милетский. Фалес считается одним из семи мудрецов, оказавших большое влияние на жизнь древних греков. Одним из самых известных его высказываний было «Познай самого себя». Именно Фалесу Милетскому приписывают доказательство о равенстве двух треугольников, имеющих равными сторону и два прилежащих к ней угла (второй признак равенства треугольников).

— Признаки равенства треугольников имели издавна важнейшее значение в геометрии, так как доказательства многочисленных теорем сводилось к доказательству равенства тех или иных треугольников.

6. Решение задач по готовому чертежу (с записью доказательства в опросных листах).

№2.1

Вопросы к учащимся:

1. Равенство каких треугольников мы можем доказать? (∆МВО=∆NСО по стороне и двум прилежащим к ней углам.)
2. Из равенства треугольников ∆МВО=∆NСО какие элементы мы возьмем? (В равных треугольниках соответственные стороны равны, значит МВ=NС)
3. Теперь мы сможем доказать равенство ∆АВМ=∆DСN? (Треугольники равны по трем сторонам)

— Запишите доказательство к этой задаче с обоснованием каждого шага (доказательство записать в опросный лист)

№2.2

Вопросы к учащимся:

1. Какой треугольник называется равнобедренным? (Равнобедренный треугольник – это треугольник, у которого две стороны равны.)
2. Как доказать равенство сторон ВО и ОС? (Из равенства треугольников ∆МВО и ∆NСО)
3. Правильно, сначала нужно доказать равенство ∆МВО=∆NСО. Как это сделать? (∆МВО=∆NСО по стороне и двум прилежащим к ней углам. В равных треугольниках соответственные стороны равны, значит ВО=ОС, значит ∆ВОС — равнобедренный, т.к. у него две стороны равны.)

— Запишите доказательство к этой задаче с обоснованием каждого шага (доказательство записать в опросный лист)

№4 (устно)

Вопросы к учащимся:

1. Что можно найти, зная, что AB= 5 см и AB=BC? (ВС=5 см)
2. Равенство каких треугольников мы можем доказать? (∆DВC=∆DFO по двум сторонам и углу между ними.)
3. Из равенства треугольников ∆DВC=∆DFO какие элементы мы возьмем? (В равных треугольниках соответственные стороны равны, значит BC=FO=5 см)
4. Что вы можете сказать о ∆FHK? (∆FHK – равнобедренный, HO – биссектриса ∆FHK, а значит и медиана ∆FHK, т.е. FO=KO=5 см. Тогда FK=10см)

6. Практическая работа учащихся.

Учащимся раздаются готовые чертежи геометрических фигур. Нужно исследовать: отметить равные отрезки и углы, выписать пары равных треугольников. Работают в опросных листах, затем следует проверка. Учитель оказывает индивидуальную помощь слабым учащихся. Можно друг у друга спросить совета. Закрепляется навык учащихся доказывать равенство треугольников, используя признаки.

Проверка осуществляется с помощью проектора. Слайды 18-20.

6. Подведение итогов урока.

— Какие цели ставили?

— Достигли их или нет

Слайд 21

• Мы изучили признаки равенства треугольников для того, чтобы…
• Мне стало понятно…
• Я понял, что смогу …
• У меня получилось …
• На следующих уроках по геометрии…

Выставление оценок учителем.

7. Домашнее задание (учебник Л.С. Атанасян, В.Ф.Бутузов и др. «Геометрия 7-9», М. Просвещение 2010)

Список использованной литературы

1. Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7- 9 классы. – М.: Просвещение, 2010.

2. Атанасян Л.С., Бутузов В.Ф., Глазков Ю.А. и др. Геометрия. Рабочая тетрадь для 7 класса. – М.: Просвещение, 2009.

3. Жохов В.И., Карташнва Г.Д., Крайнева Л.Б. Уроки геометрии в 7-9 классах: Методические рекомендации для учителя к учебнику Атанасяна Л.С. и др. – М.: Вербум-М, 2004.

4. Атанасян Л.С., Бутузов В.Ф., Глазков Ю.А. и др. Изучение геометрии в 7, 8, 9 классах: Метод. Рекомендации к учебнику: Книга для учителя. – М.: Просвещение, 2009.

5. Зив Б.Г., Мейлер В.М. Дидактические материалы по геометрии 7 класс. – М.: Просвещение, 2006.

📸 Видео

Задачи на доказательство равенства треугольников. Первый признак. Простые.Скачать

Геометрия 7 класс. Тема: "Решение задач на применение признаков равенства треугольников".Скачать

Геометрия 7. Урок 8 - Признаки равенства треугольников.Скачать

7 класс, 20 урок, Третий признак равенства треугольниковСкачать

Второй признак равенства треугольников. 7 класс.Скачать

7 класс, 36 урок, Признаки равенства прямоугольных треугольниковСкачать