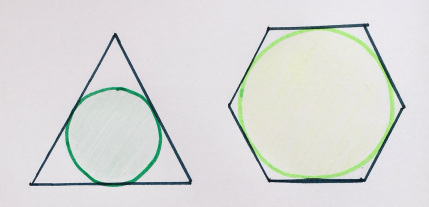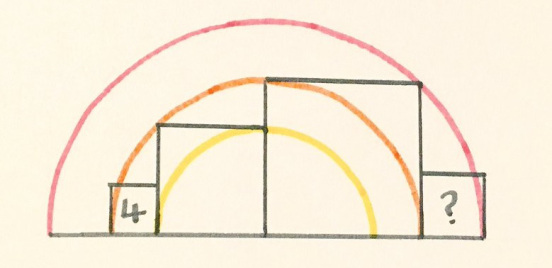Интересные задачи с треугольниками

Наглядная геометрия 7 класс. Ключевые задачи по теме Треугольники

Запомните!

1. Признаки равенства треугольников.

• 1-й. По двум сторонам и углу между ними.
• 2-й. По стороне и двум прилежащим к ней углам.
• 3-й. По трем сторонам.

2. Свойство углов равнобедренного треугольника.

Углы при основании равнобедренного треугольника равны.

3. Обратная теорема.

Если два угла треугольника равны, то треугольник равнобедренный.

4. Свойство биссектрисы равнобедренного треугольника.

Биссектриса, высота и медиана равнобедренного треугольника, проведенные из вершины к основанию, совпадают.

5. Признаки равнобедренного треугольника. Треугольник является равнобедренным, если:

• а) высота является и медианой;
• б) высота является и биссектрисой;
• в) биссектриса является и медианой.

6. Теорема о свойстве точек серединного перпендикуляра.

• Любая точка серединного перпендикуляра равноудалена от концов отрезка.
• Если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре к нему.

7. Теорема о пересечении серединных перпендикуляров.

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке — центре описанной около треугольника окружности.

Простые вопросы по теме «Треугольники»

1. В треугольнике провели медиану. Сколько треугольников изображено на рисунке?
2. Если стороны треугольника продлить, то сколько углов всего образуется, не считая развернутых? А считая и развернутые?
3. Верно ли, что биссектриса треугольника лежит на биссектрисе угла?
4. Может ли высота треугольника делить сторону пополам?
5. Может ли биссектриса треугольника быть перпендикулярной стороне треугольника?
6. Верно ли утверждение: «Биссектриса равнобедренного треугольника является высотой и медианой»?
7. Является ли любой равнобедренный треугольник равносторонним?
8. Является ли любой равносторонний треугольник равнобедренным?
9. Может ли биссектриса некоторого равнобедренного треугольника, проведенная к боковой стороне, быть медианой?
10. Может ли высота треугольника быть равна его медиане, проведенной из той же вершины?
11. Может ли биссектриса треугольника быть равна его высоте, проведенной из той же вершины?
12. Существует ли треугольник, периметр которого в 3 раза больше одной из сторон?
13. Если медиана образует равные углы с соседними сторонами треугольника, то какой угол она образует с третьей стороной?
14. Что для студентов означает слово «медиум»?
15. Сколько всего теорем в данной теме?

Непростые вопросы по теме «Треугольники»

16* В треугольнике провели 2 медианы. Сколько треугольников изображено на рисунке?
17* В треугольнике провели 3 медианы. Сколько треугольников изображено на рисунке?
18* Может ли в треугольнике высота являться медианой, но не являться биссектрисой?
19* Как звучит теорема о свойстве углов равнобедренного треугольника в форме «Если …, то …»?
20* Как звучит утверждение, обратное теореме о свойстве углов равнобедренного треугольника, в форме «Если …, то …»?
21* Может ли медиана треугольника равняться соседней стороне?
22* Может ли биссектриса треугольника равняться соседней стороне?
23* Может ли высота треугольника равняться соседней стороне?
24* Может ли серединный перпендикуляр к стороне треугольника иметь общую точку с каждой из двух других сторон?
25* Может ли серединный перпендикуляр к стороне треугольника делить противоположный угол треугольника пополам?

Ответы на простые и непростые вопросы

1. Три. Два маленьких и один данный.
2. 12; 24.
3. Да.
4. Да. В равнобедренном треугольнике.
5. Да. В равнобедренном треугольнике.
6. Нет. Только биссектриса, проведенная из вершины к основанию.
7. Нет.
8. Да.
9. Да. Если треугольник равносторонний.
10. Да. В равнобедренном треугольнике это высота, проведенная к его основанию.
11. Да. В равнобедренном треугольнике это биссектриса, проведенная к его основанию.
12. Да. Например, равносторонний.
13. 90°. Если медиана является биссектрисой, то треугольник равнобедренный и эта медиана является и высотой, проведенной к основанию.
14. Медиум — студенческий праздник, знаменующий середину учебы.
15. Тринадцать теорем, включая задачу о пересечении серединных перпендикуляров к сторонам треугольника.

16* 8.
17* 16.
18* Нет. Если высота является медианой, то треугольник равнобедренный и эта высота является и биссектрисой.
19* «Если треугольник равнобедренный, то углы при основании равны». 20* «Если у треугольника два угла равны, то треугольник равнобедренный».
21* Да.
22* Да.
23* Да. В прямоугольном треугольнике.
24* Да. В равнобедренном прямоугольном треугольнике.
25* Да. Если треугольник равнобедренный.

Это конспект по геометрии «Ключевые задачи по теме Треугольники». Выберите дальнейшие действия:

Видео:Найдите угол: задача по геометрииСкачать

Двадцать задачек (по безумной, восхитительной геометрии)

Предупреждение врача. Остерегайтесь этих головоломок. Побочные эффекты могут включать потерянное послеобеденное время, скомканные волосы и восклицания «А-а-а-х, вот как это делается» настолько громкие, что могут треснуть оконные стёкла.

Несколько месяцев назад я наткнулся в твиттере на математические головоломки Катрионы Ширер. Они сразу меня увлекли: каждая головоломка такая осязаемая, ручной работы, словно просит её решить. И на каждую вы можете легко потратить час времени, а то и больше.

Катриона разрешила мне подвесить вас на эти задачки — и поделилась 20 своими любимыми головоломками. Она даже удовлетворила моё любопытство и восхищение, дав интервью (см. в конце статьи).

Наслаждайтесь. И не говорите, что врач не предупреждал.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

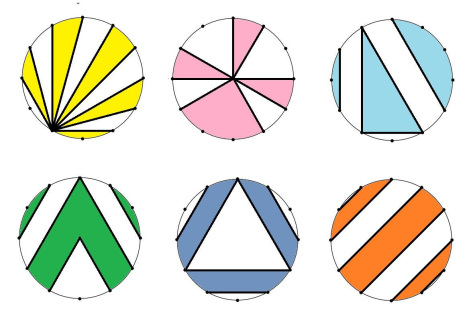
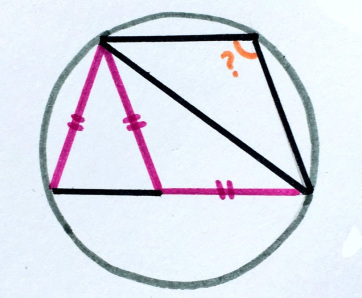
1. Сад часов

Какая часть каждого круга закрашена? (12 точек на равном расстоянии; единственная точка внутри круга — его центр)

«К сожалению, из эти шести моя любимая — единственная, которую я не придумала сама, — говорит Катриона, — это тёмно-синяя».

Видео:Задача, которую исключили из экзамена в АмерикеСкачать

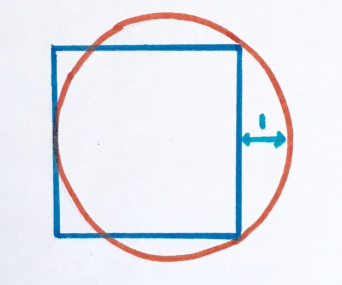
2. Опрокинутый квадрат

(Как по мне, это классика).

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

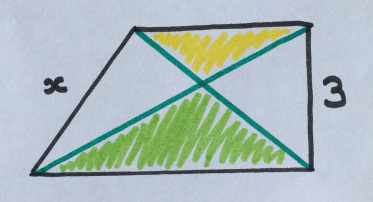
3. Это ловушка

В прямоугольной трапеции зелёная область на 6 больше, чем жёлтая. Чему равен x?

«Это „вторая версия” данной головоломки: она лучше, чем первая, которую я придумала».

Видео:Этой задачей русские дети 10 лет мучили американцев. Американцы не понимали, что делают не такСкачать

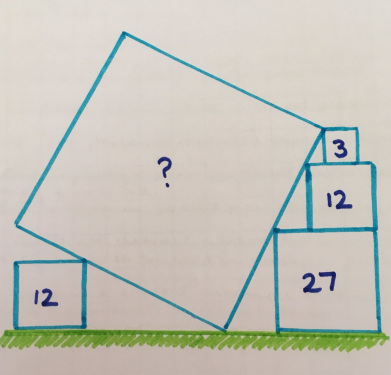
4. Три квадратных тарелки

Длины сторон трёх квадратов — последовательные целые числа. Какова общая площадь?

«Эта мне очень нравится: на её основе я нарисовала много красивых узоров».

Видео:Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

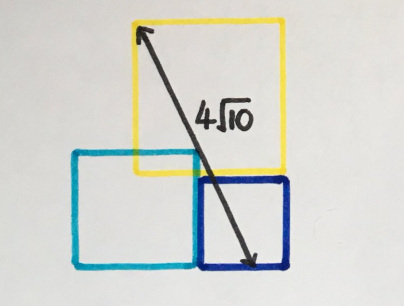
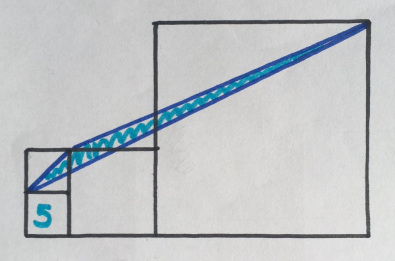
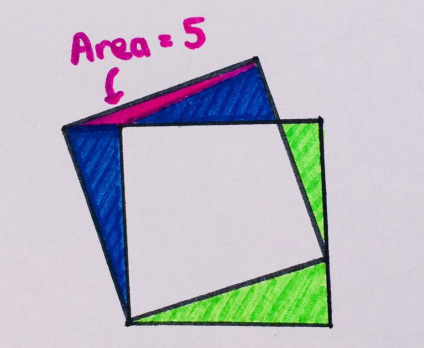
5. Красивая стрижка

Площадь левого нижнего квадрата 5. Какова площадь синего треугольника?

«Наверное, моя любимая за всё время. Выглядит просто невозможным! Здесь метод решения называется «стрижка», shearing (к сожалению, не в мою честь)».

Видео:Как появился знаменитый треугольник Карпмана? Психологическое значение библейских историй. Лекция №2Скачать

6. Все люди рождены равными

«Ещё одна переделка, которую я предпочитаю оригиналу».

Видео:КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать

7. Полукруг турдакен

«Головоломки с углами гораздо труднее составлять. Ученики сказали, что это довольно простая задачка, но мои родители испытали большие трудности. Кажется, эта головоломка требует больше „знаний”, но сам процесс решения проще».

Видео:Треугольники. Практическая часть - решение задачи. 7 класс.Скачать

8. Степенные хорды

Какова площадь круга?

«В школе я не изучала теорему о пересекающихся хордах, поэтому люблю везде её использовать!»

Видео:Задача с чешской олимпиады, которую решили только 14 школьниковСкачать

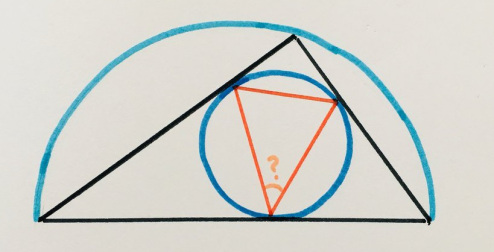
9. Сказка о двух кругах

У этих правильных многоугольников одинаковый периметр. Найдите отношение площадей вписанных окружностей.

«Это следствие другой головоломки, но она мне нравится больше, чем оригинал!»

Видео:Две задачи по геометрии за 7 класс на тему: "Треугольники"Скачать

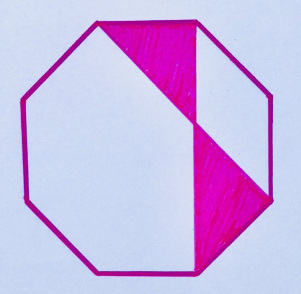
10. Doc Oct

У закрашенной области такое же значение, как у периметра правильного восьмиугольника. Каково значение?

«Думаю, это довольно чистая задачка, хотя выглядит как массовое разграбление головоломок Эда Сауталла».

Видео:Найдите угол: задача по геометрииСкачать

11. Всё в квадрате

«Мне нравится то, что хотя вы здесь можете найти все стороны оранжевого треугольника (и я это сделала, когда решала), но на самом деле это не нужно — достаточно площади и гипотенузы».

Видео:Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать

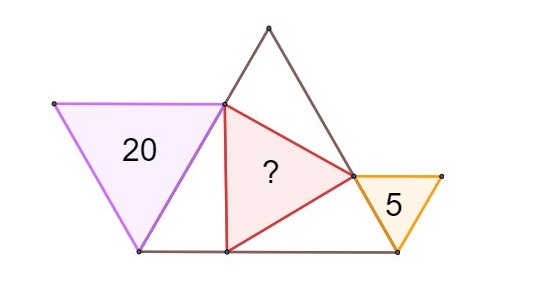
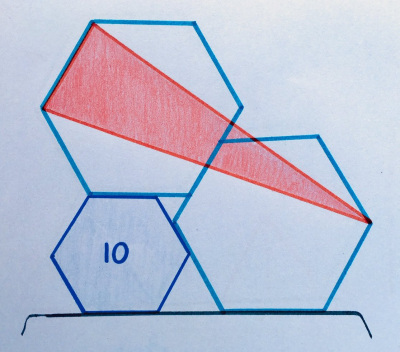
12. Шип в улье

Два из правильных шестиугольников идентичны; у третьего площадь 10. Какова площадь красного треугольника?

«Довольно неплохо: мне нравится, что не нужно иметь дело с любой длиной стороны, которые почти наверняка ужасны».

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

13. Я видел равнобедренных

Все четыре треугольника равнобедренные. Найдите угол.

«Думаю, что формулировка этой задачки идеальна. Многие пропускают важную информацию и приходят к выводу, что есть бесконечное число решений!»

Видео:Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

14. Зеленый против синего

На картинке больше зелёного цвета или синего (и на сколько)?

«Ещё одна из моих любимых».

Видео:Решали пол-урока, а оказалось очень простоСкачать

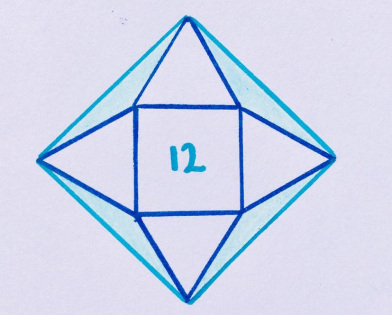
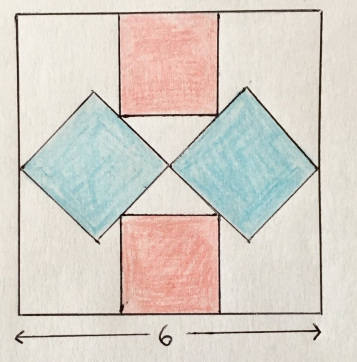
15. Резцы по камню

Четыре равносторонних треугольника расположены вокруг квадрата с площадью 12. Какова закрашенная площадь?

«Тут самое лучшее — действительно хорошие решения по рассечению площади».

Видео:🔥 ФОКУС с треугольником #shortsСкачать

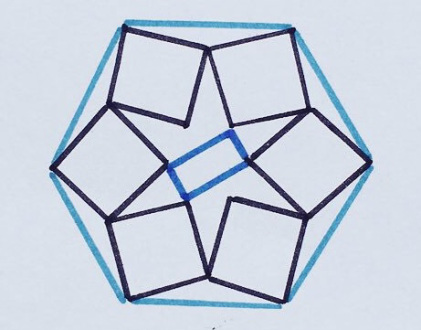
16. Едем, едем, уехалиугольник

Шесть одинаковых квадратов и меньший прямоугольник вписаны в этот правильный шестиугольник. Какую часть шестиугольника они занимают?

«Здесь ответ не такой красивый, но очень удивил меня. Думаю, из-за своей сложности эта задачка не получила такого распространения в твиттере, как другие!»

Видео:ЗАДАЧА ВЗОРВАЛА ИНТЕРНЕТ! НИКТО НЕ РЕШИЛ!Скачать

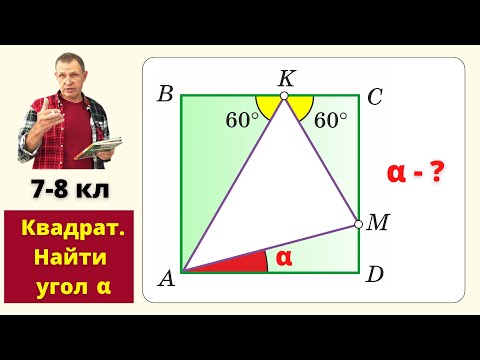
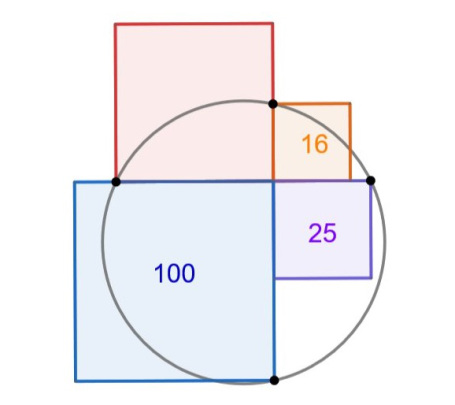
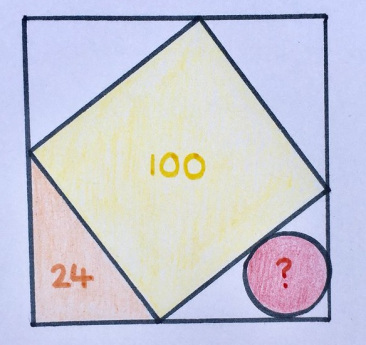
17. Только один факт

Какова площадь этого квадрата?

«Это одна из моих любимых, потому что сначала кажется, что информации недостаточно».

Видео:Решение задач на тему "Подобные треугольники". 8 классСкачать

18. Стиральная машина

Какая часть большого квадрата закрашена?

«Здесь мне нравится сумбур квадратов, как они грохочут вокруг словно в стиралке. И ответ тоже удивительно красивый».

Видео:Как за 5 секунд решать такие задачи с треугольникиСкачать

19. Летающие флаги

У квадратов одного цвета одинаковый размер. Какова площадь всех закрашенных областей?

«Это довольно просто, как только вы поймёте — но я поняла не сразу, поэтому простота ответа меня удивила».

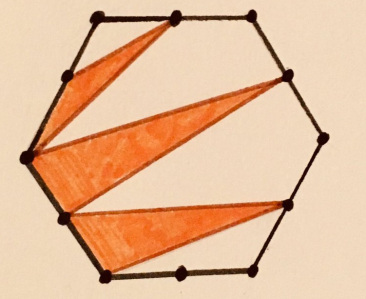
20. Тигрогон

Какая часть фигуры закрашена? Шестиугольник правильный, с равномерно расположенными точками по периметру.

«Эту я редко публиковала. Но картинка напоминает мне Тигра Тони [с пачек быстрого завтрака Kellogg — прим. пер.]».

БОНУС:

Закат над Квадратным городом

У левого квадрата площадь 4. Какова площадь правого квадрата?

«Мне нравится эта задачка, она напоминает закат над городом скверов.”

Если вы дочитали до этого места — возможно, через 6 месяцев после начала чтения — и ваш стол окружен скомканными бумагами и пустыми китайскими контейнерами для продуктов питания, то вам будет приятно почитать небольшое интервью с Катрионой.

Как вы пришли к разработке своих головоломок?

Я поехала в отпуск в Шотландское высокогорье, но забыла взять пальто, поэтому пришлось сидеть в домике в одиночестве, пока друзья гуляли на природе! Ничего не оставалось, кроме как машинально чертить линии на бумажке.

Не ожидала, что это превратится в хобби, но это немного затягивает, особенно когда люди присылают в ответ свои решения, которые мне нравятся. Почти всегда можно красиво сократить головоломку, что я пропустила.

Как проходит творческий процесс?

Всё начинается с рисования бессмысленных фигурок. В итоге получается целая страница перекрывающихся квадратов под разными углами или правильных (типа) пятиугольников с разными закрашенными частями, а потом я смотрю, есть ли там какая- то хорошая математика — отношения между длинами или площадями или углами.

Многие из ваших задачек нарисованы маркером на бумаге. Почему такой лоутек?

Я пробовала использовать Desmos и Geogebra, но не очень понравилось. По-моему, быстрее нарисовать вписанный круг вручную, после небольшого количества проб и ошибок, чем красиво строить его в геометрии программного обеспечения.

Кроме того, при использовании фломастера вы можете выдумывать вещи, потому что линии настолько толстые. Это хороший компромисс между тем, чтобы выглядеть «правильно», но также знать, что вы не можете просто вытащить линейку и измерить фигуру.

Одна из приятных вещей в геометрии — что она многое прощает. Я могу показать вам безнадёжный квадрат или круг, но этого достаточно, чтобы передать концепцию, потому что они так хорошо определены.

Некоторые из ваших головоломок дают самый минимум информации. Как вы находите эту границу, где диаграмма как раз определена?

Иногда этот минимум на самом деле подсказка, потому что он отправляет вас по одной дороге. Я предпочитаю давать чуть больше необходимого, поэтому есть несколько обманных маршрутов. Это также даёт большее разнообразие решений!

Было дело, я опубликовала пару невозможных головоломок: к счастью, кто-нибудь обычно указывает на это довольно быстро!

Я также публиковала задачки с массивным количеством излишней информации, потому что не видела хорошего решения, чтобы использовать только половину информации.

Советы для потенциальных создателей головоломок?

Отлично, тут мой синдром самозванца полностью проявится. Я определённо ещё новичок — я занимаюсь этим только с августа [статья опубликована в октябре 2018 года — прим. пер.]! С другой стороны, мне нравится создавать головоломки и читать решения даже больше, чем решать их самой.

Основной целью головоломки должно быть развлечение — вот что отличает её от стандартной математической задачи. Таким образом, вам нужно по крайней мере два из трёх:

1. Красивая постановка задачи. Предоставьте минимум информации, чтобы читателю стало интересно, как вообще можно решить такую задачу. Или несколько дразнящих кусочков информации, каждый из которых якобы предлагает способ решения. Правильные многоугольники и круги — фантастические штуки, потому что скрывают огромное количество информации.
2. Красивый метод. Трюк или кратчайший путь, или внезапное озарение, которое всё упрощает. Это может быть не самый очевидный метод. Я видела много задачек, которые решаются с помощью алгебры или иррациональных чисел, или ужасных выражений с pi, а в конце всё внезапно сокращается — и я понимаю, что есть более простой способ.
3. Красивый ответ. Мало удовольствия работать над головоломкой, чтобы в конце получить некрасивый ответ.

В принципе, начните рисовать — найдите головоломку, которую вам понравилось решать, и подумайте, как можно её расширить или изменить некоторые элементы. Если вдруг попадутся соотношения, которые вас удивляют, то с высокой вероятностью они удивят и других. Twitter — отличная платформа, так как люди могут публиковать в ответ собственные картинки.

Решение задач по теме «Треугольники» (7-й класс)

Разделы: Математика

Класс: 7

Цели и задачи урока:

• обобщить, закрепить и углубить знания по изученной теме;
• формировать умение обучаемых доказывать равенство данных треугольников, опираясь на изученные признаки, применять свойства равнобедренного треугольника;
• отработать навыки решения простейших задач на построение с помощью циркуля и линейки;

• развивать логическое мышление, самостоятельность учащихся при решении заданий; умение на практике применять знания, полученные на уроках;

• воспитывать познавательную активность, упорство в достижении поставленной цели, культуру умственного труда

Оборудование:

• интерактивная доска или наглядный материал (готовые чертежи);
• карточки с задачами для индивидуальной работы на доске;
• таблицы с признаками равенства треугольников.

Тип урока: урок закрепления полученных знаний.

Ход урока

І. Организационный момент.

Учитель:

— Тема урока: «Решение задач по теме «Треугольники»». Мы сегодня обобщим и систематизируем знания по данной теме и наша цель: подготовиться к контрольной работе, которая будет на следующем уроке.

— Откройте дневники и запишите домашнее задание.

• I уровень: № 120(б), 121;
• II – III уровень: №160 (б), 162(б).

II. Актуализация опорных знаний.

1. У доски двое учащихся решают задачи по карточкам.

Начертите равнобедренный треугольник АВС с основанием АС. С помощью циркуля и линейки проведите медиану АА1 к боковой стороне ВС.

Дано: АО = BO, СО = DO, CO = 5см, ВО = 3см, BD = 4см.
1)Докажите, что САО = DBO.
2)Найдите периметр треугольника САО.

2. Для остальных учащихся класса организована фронтальная работа.

Цель: повторить основные вопросы теории темы «Равнобедренный треугольник и его свойства» с помощью теста. (Вопросы теста – на интерактивной доске)

Теоретический тест. [1]
В каждом задании из трёх предложенных ответов выберите верный и обоснуйте его. Верных ответов может быть несколько. Подумайте и ответьте на вопрос. (А я считаю, что…; я не согласна с этим утверждением, т.к. …)

1) Медиана в равнобедренном треугольнике является его биссектрисой и высотой. Это утверждение:
а) всегда верно;
б) может быть верно;
в) всегда неверно.
Ответ: б), если медиана проведена к основанию равнобедренного треугольника.

2) Если треугольник равносторонний, то:
а) он равнобедренный;
б) все его углы равны;
в) любая его высота является биссектрисой и медианой.
Ответ: а), б), и в), равносторонний треугольник является частным случаем равнобедренного треугольника; в равнобедренном треугольнике углы при основании равны, поэтому в равностороннем треугольнике все углы равны.

3) В каком треугольнике только одна его высота делит треугольник на два равных треугольника?
а) в любом;
б) в равнобедренном;
в) в равностороннем.
Ответ: б), высота, проведённая к основанию равнобедренного треугольника.

4) Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение:
а) всегда верно;
б) может быть верно;
в) всегда неверно.
Ответ: а)

5) Если треугольник равнобедренный, то
а) он равносторонний;
б) любая его медиана является биссектрисой и высотой;
в) ответы а) и б) неверны.
Ответ: в), т.к. равнобедренный треугольник не всегда является равносторонним; медиана, проведённая к боковой стороне равнобедренного треугольника, не является биссектрисой и высотой, если треугольник не равносторонний.

6) В каком треугольнике любая его высота делит треугольник на два равных треугольника?
а) в любом;
б) в равнобедренном;
в) в равностороннем.
Ответ: в).

Учитель:
— Мы с вами повторили материал темы «Равнобедренный треугольник и его свойства», а теперь повторим признаки равенства треугольников. (Обратить внимание обучающихся на таблицы с признаками равенства треугольников)

3. Задачи в рисунках (на интерактивной доске).

Учитель:
— Определите, являются ли равными треугольники на рисунках.

— Сколько пар равных элементов должно быть в равных треугольниках?