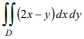Интеграл по области треугольника (6 видео)

Задача 61184 Вычислить интеграл , где область D –.

Содержание

Условие
Решение
Вычисление двойных интегралов: теория и примеры
Что значит вычислить двойной интеграл?
Сведение двойного интеграла к повторному
Случай прямоугольной области
Случай криволинейной или треугольной области
Вычислить двойной интеграл самостоятельно, а затем посмотреть решение
x-правильная и неправильная, y-правильная и неправильная области интегрирования
Смена порядка интегрирования
Вычисление площади и объёма с помощью двойных интегралов
Так что же такое двойной интеграл?
Двойной интеграл по треугольнику
Введите подинтегральную функцию, для которой необходимо вычислить двойной интеграл
Правила ввода выражений и функций
🎦 Видео

Условие

Вычислить интеграл , где область
D – треугольник с вершинами A(-1;2), B(3;4), C(6;2)

Решение

Область D рассматриваем как область горизонтального входа

Составляем уравнение прямой АВ как прямой, проходящей через две точки

⇒
x=2y-5 — уравнение линии входа в область

Составляем уравнение прямой ВC как прямой, проходящей через две точки

⇒
x=(-3/2)y+6 — уравнение линии выхода

=∫ ^(4)_(2) ([b]((2y-5)^2-y*(2y-5)-((-3/2)y+6)^2-y*( (-3/2)y+6))dy=[/b])dy

Видео:Двойной интеграл / Как находить двойной интеграл через повторный (двукратный) / Два способаСкачать

Вычисление двойных интегралов: теория и примеры

Видео:Вычислить двойной интеграл по области, ограниченной линиями ∫∫(5x+y)dxdy D: y=x^3, y=0, x=3.Скачать

Что значит вычислить двойной интеграл?

Двойные интегралы – это обобщение понятия определённого интеграла для функции двух переменных, заданной как z = f(x, y) .

Записывается двойной интеграл так:

Здесь D – плоская фигура, ограниченная линиями, выражения которых (равенства) даны в задании вычисления двойного интеграла. Слева и справа – равенствами, в которых слева переменная x , а сверху и снизу – равенствами, в которых слева переменная y . Это место и далее – одно из важнейших для понимания техники вычисления двойного интеграла.

Вычислить двойной интеграл — значит найти число, равное площади упомянутой фигуры D .

Пока мы не касаемся определения двойного интеграла, а будем учиться его вычислять. Понять, что такое двойной интеграл, проще, когда решены несколько задач на его вычисление, поэтому определение двойного интеграла вы найдёте в конце этого урока. Чуть забегая вперёд, можно лишь отметить, что определение двойного интеграла также связано с упоминавшейся фигурой D .

В случае если фигура D представляет собой прямоугольник, все линии, ограничивающие её – это прямые линии. Если фигура D — криволинейна, то слева и справа она ограничена прямыми, а сверху и снизу – кривыми линиями, заданными равенствами, которые даны в задании. Бывают и случаи, когда фигура D – треугольник, но о таких случаях чуть дальше.

Для вычисления двойного интеграла нужно, таким образом, рассортировать линии, огранивающие фигуру D , которая имеет строгое название – область интегрирования. Рассортировать на левые и правые и на верхние и нижние. Это потребуется при сведении двойного интеграла к повторному интегралу – методе вычисления двойного интеграла.

Случай прямоугольной области:

Случай криволинейной области:

А это уже решение знакомых нам определённых интегралов, в которых заданы верхний и нижний пределы интегрирования. Выражения, задающие линии, которые ограничивают фигуру D , будут пределами интегрирования для обычных определённых интегралов, к которым мы уже подходим.

Видео:Вычислить двойной интеграл по областиСкачать

Сведение двойного интеграла к повторному

Случай прямоугольной области

Пусть дана функция двух переменных f(x, y) и ограничения для D : D = <(x; y) | a ≤ x ≤ b; c ≤ y ≤ d> , означающие, что фигуру D слева и справа ограничивают прямые x = a и x = b , а снизу и сверху — прямые y = c и y = d . Здесь a, b, c, d — числа.

Пусть для такой функции существует двойной интеграл

Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид

Здесь пределы интегрирования a, b, c, d — числа, о которых только что упоминалось.

Сначала нужно вычислять внутренний (правый) определённый интеграл, затем — внешний (левый) определённый интеграл.

Можно и поменять ролями x и y. Тогда повторный интеграл будет иметь вид

Такой повторный интеграл нужно решать точно так же: сначала — внутренний (правый) интеграл, затем — внешний (левый).

Пример 1. Вычислить двойной интеграл

Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:

Вычисляем внутренний (правый) интеграл, считая игрек константой. Пользуемся формулой 7 из таблицы интегралов. Получаем.

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого), пользуясь для каждого слагаемого той же формулой 7:

Результат и будет решением данного двойного интеграла.

Пример 2. Вычислить двойной интеграл

Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:

Вычисляем внутренний (правый) интеграл, считая икс константой. Пользуясь формулой 9 из таблицы неопределенных интегралов, получаем

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого). Пользуемся формулой 10 из таблицы неопределенных интегралов и формулой Ньютона-Лейбница для вычисления определенного интеграла:

Результат и будет решением данного двойного интеграла.

Случай криволинейной или треугольной области

Пусть снова дана функция двух переменных f(x, y) , а ограничения для D : уже несколько другого вида:

Эта запись означает, что фигуру D слева и справа ограничивают, как и в случае прямолинейной области — прямые x = a и x = b , но снизу и сверху — кривые, которые заданы уравнениями и . Иными словами, и — функции.

Пусть для такой функции также существует двойной интеграл

Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид

Здесь пределы интегрирования a и b — числа, а и — функции. В случае треугольной области одна из функций или — это уравнение прямой линии. Такой случай будет разобран в примере 3.

Как и в случае прямолинейной области, сначала нужно вычислять правый определённый интеграл, затем — левый определённый интеграл.

Точно так же можно поменять ролями x и y. Тогда повторный интеграл будет иметь вид

Пример 3. Вычислить двойной интеграл

Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования и видим, что она треугольная:

Вычисляем внутренний (правый) интеграл, считая икс константой. Пользуясь формулами 6 и 7 из таблицы неопределенных интегралов, получаем

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого). Сначала представляем этот интеграл в виде суммы интегралов:

Вычисляем второе слагаемое, пользуясь все той же формулой:

Вычисляем третье слагаемое, также по формуле 7:

Получаем сумму, которая и будет решением данного двойного интеграла:

Пример 4. Вычислить двойной интеграл

Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:

Пользуясь формулой Ньютона-Лейбница, вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.

Теперь, пользуясь формулой 7 из таблицы неопределенных интегралов, вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):

Результат и будет решением данного двойного интеграла.

Видео:Математика без ху!ни. Двойные интегралы. Часть1. Как вычислять.Скачать

Вычислить двойной интеграл самостоятельно, а затем посмотреть решение

Пример 5. Вычислить двойной интеграл

если область D ограничена прямыми

Пример 6. Вычислить двойной интеграл

если область D ограничена прямыми

Видео:Математический анализ, 41 урок, Вычисление двойных интеграловСкачать

x-правильная и неправильная, y-правильная и неправильная области интегрирования

Случается, область интегрирования двойного интеграла ограничена такими линиями, что возникает необходимость разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно. Это случаи, когда:

1) область интегрирования представляет собой фигуру, имеющую в виде нижней или верхней (левой или правой) границы две или более двух прямых или кривых линий;

2) область интегрирования представляет собой фигуру, границу которой прямые пересекают более чем в двух точках.

Если вышесказанное относится к левой или правой границе области интегрирования, то есть ограничениях, заданных линиями, выраженными через x, то область интегрирования называется x-неправильной. Если же прямая y = y 0 пересекает соответствующую границу лишь в одной точке и если границей служит лишь одна прямая или кривая, то область интегрирования называется x-правильной

Аналогично, если границу, заданную линиями, выраженными через y, прямая x = x 0 пересекает более чем в одной точке или если границей служат более одной прямой или кривой, то область интегрирования называется y-неправильной. Вывести теперь признаки y-правильной области, надо полагать, совсем просто.

До сих пор мы рассматривали примеры с x-неправильными и y-правильными областями интегрирования. Теперь рассмотрим случаи, когда условие правильности нарушается.

Пример 7. Вычислить двойной интеграл , область интегрирования которого ограничена линиями y = x , xy = 1 , y = 2 .

Решение. Область интегрирования является y-неправильной, так как её нижнюю границу нельзя задать одной линией y = y(x) . Как видно на рисунке выше, нижняя граница складывается из y = x (тёмно-бордовая) и xy = 1 (зелёная). Поэтому прямой x = 1 (чёрная) можем разбить область интегрирования на две части — и .

Вычисляется этот двойной интеграл так:

Видео:Формула ГринаСкачать

Смена порядка интегрирования

Как уже отмечалось выше, после приведения двойного интеграла к повторному интегралу, можно поменять переменные x и y ролями, или, говоря иначе, поменять порядок интегрирования.

Смена порядка интегрирования образно может быть описана следующими словами О’Генри: «Так ведёт себя обитатель джунглей — зверь, попав в клетку, и так ведёт себя обитатель клетки — человек, заблудившись в джунглях сомнений». Результат, так же по О’Генри один и тот же: «Чалмерс разорвал письмо на тысячу мельчайших клочков и принялся терзать свой дорогой ковёр, расхаживая по нему взад и вперёд». (О’Генри. Шехерезада с Мэдисон-сквера.)

Тогда, если левый интеграл у нас по переменной x, а правый — по y, то после смены порядка интегрирования всё будет наоборот. Тогда пределы интегрирования для «нового» игрека нужно «позаимствовать» у «старого» икса, а пределы интегрирования для «нового» икса получить в виде обратной функции, разрешив относительно икса уравнение, задававшее предел для игрека.

Пример 8. Сменить порядок интегрирования для повторного интеграла

Решение. После смены порядка интегрирования интеграл по игреку станет левым, а интеграл по иксу — правым. Пределы интегрирования для «нового» игрека позаимствуем у «старого» икса, то есть нижний предел равен нулю, а верхний — единице. Пределы интегрирования для «старого» игрека заданы уравнениями и . Разрешив эти уравнения относительно икса, получим новые пределы интегрирования для икса:

(нижний) и (верхний).

Таким образом, после смены порядка интегрирования повторный интеграл запишется так:

После смены порядка интегрирования в двойном интеграле нередко область интегрирования превращается в y-неправильную или x-неправильную (см. предыдущий параграф). Тогда требуется разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно.

Поскольку разбиение области интегрирования на части представляет определённые трудности для многих студентов, то не ограничимся примером, приведённым в предыдущем параграфе, а разберём ещё пару примеров.

Пример 9. Сменить порядок интегрирования для повторного интеграла

Решение. Итак, область интегрирования данного повторного интеграла ограничена прямыми y = 1 , y = 3 , x = 0 , x = 2y .

При интегрировании в другом порядке нижняя граница области состоит из двух прямых: AB и BC , которые заданы уравнениями y = 1 и y = x/2 , что видно на рисунке ниже.

Выход из такой неопределённости состоит в разбиении области интегрирования на две части. Делить область интегрирования будет прямая BМ . Новые пределы интегрирования вычисляем, находя обратную функцию. Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме двух интегралов:

Естественно, таким же будет решение двойного интеграла, который сводится к повторному интегралу, данному в условии этого примера.

Пример 10. Сменить порядок интегрирования для повторного интеграла

Решение. Итак, область интегрирования повторного интеграла ограничена прямыми x = 0 , x = 2 и кривыми и .

Как видно на рисунке ниже, прямая, параллельная оси 0x , будет пересекать нижнюю границу области интегрирования более чем в двух точках.

Поэтому разобьём область интегрирования на три части прямыми, которые на рисунке начерчены чёрным. Новые пределы интегрирования вычисляем, находя обратную функцию. Пределы для трёх новых областей интегрирования будут следующими.

Для :

Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме трёх интегралов:

Той же сумме трёх интегралов будет равен и двойной интеграл, который сводится к повторному интегралу, данному в условии этого примера.

И всё же обстоятельства непреодолимой силы нередко мешают студентам уже на предыдущем шаге — расстановке пределов интегрирования. Тревога и смятение не лишены некоторого основания: если для разбиения области интегрирования на части обычно достаточно приглядеться к чертежу, а для решения повторного интеграла — таблицы интегралов, то в расстановке пределов интегрирования нужен некоторый опыт тренировок. Пробежим пример, в котором остановимся только на расстановке пределов интегрирования и — почти на автомате — на разбиении области и опустим само решение.

Пример 11. Найти пределы интегрирования двойного интеграла, если область интегрирования D задана следующим образом:

Решение. В явном виде (через x и y «без примесей») линии, ограничивающие область интегрирования, не заданы. Так как для икса ими чаще всего оказываются прямые, касающиеся в одной точке верхней и нижней границ, выраженных через игрек, то пойдём именно по этому пути. Тем более, что при смене порядка интегирования мы получим область интегрирования с такой же площадью. Разрешим неравенства относительно игрека и получим:

Строим полученные линии на чертёже. Пределами интегрирования по иксу действительно служат линии x = 0 и x = 2 . Но область интегрирования оказалась y-неправильной, так как её верхнюю границу нельзя задать одной линией y = y(x) .

Поэтому разобьём область интегрирования на две части при помощи прямой x = 1 (на чертеже — чёрного цвета).

Теперь данный двойной интеграл можем записать как сумму двух повторных интегралов с правильно расставленными пределами интегрирования:

Видео:Вычисление двойного интегралаСкачать

Вычисление площади и объёма с помощью двойных интегралов

В этом параграфе даны примеры, в которых двойной интеграл равен отрицательному числу. Но, как отмечалось в теоретической справке в начале урока, площадь области интегрирования равна самому двойному интегралу. А если двойной интеграл — отрицательное число, то площадь равна его модулю.

Вычисление площади плоской фигуры с помощью двойного интеграла имеет более универсальный характер, чем вычисление площади криволинейной трапеции с помощью определённого интеграла. С помощью двойного интеграла можно вычислять площади не только криволинейной трапеции, но и фигур, расположенных произвольно по отношению к к координатным осям.

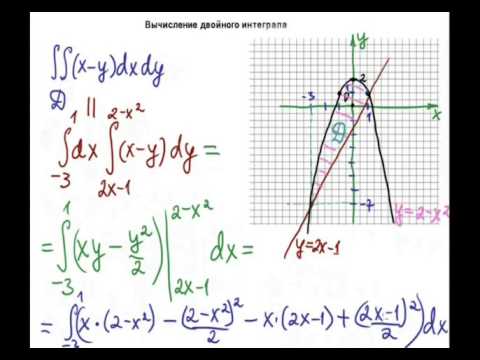
Пример 12. Вычислить площадь области, ограниченной линиями y² = x + 1 и x + y = 1 .

Решение. Область интегрирования представляет собой фигуру, ограниченную слева параболой y² = x + 1 , а справа прямой y = 1 — x . (рисунок ниже).

Решая как систему уравнения этих линий, получаем точки их пересечения: . Ординаты этих точек — — 2 и 1 будут соответственно нижним и верхним пределами интегрирования по игреку. Итак, площадь фигуры найдём как двойной интеграл, сведённый к повторному:

Вычисляем внутренний (правый) интеграл:

Вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):

Как видим, решение двойного интеграла — отрицательное число. За площадь данной плоской фигуры принимается модуль этого числа, то есть 4/9.

Объём криволинейного цилиндра, ограниченного сверху поверхностью , снизу плоскостью z = 0 и с боковых сторон цилиндрической поверхностью, у которой образующие параллельны оси 0z , а направляющей служит контур области, вычисляется также по формуле двойного интеграла. То есть, с помощью двойного интеграла можно вычислять объёмы тел.

Пример 13. Вычислить объём тела, ограниченного поверхностями x = 0 , y = 0 , z = 0 и x + y + z = 1 (рисунок ниже).

Расставляя пределы интегрирования, получаем следующий повторный интеграл:

Вычисляем внутренний (правый) интеграл:

Вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):

Вновь видим, что решение двойного интеграла — отрицательное число. За объём данного тела принимается модуль этого числа, то есть 1/6.

Видео:Двойной интеграл / Как находить двойной интегралСкачать

Так что же такое двойной интеграл?

Мы уже знаем, что представляет собой область D. Пусть z = f(x, y) — некоторая функция двух переменных, определённая и ограниченная в этой области. Разобъём область D произвольно на n частей, не имеющих общих точек, с площадями . В каждой из этих частей выберем произвольную точку и составим сумму

которую назовём интегральной суммой. Диаметром области D условимся называть наибольшее расстояние между граничными точками этой области. Учитывается также наибольший из диаметров частичных областей.

Определение. Если интегральная сумма при неограниченном возрастании числа n разбиений области D и стремлении наибольшего из диаметров частичных областей к нулю имеет предел, то этот предел называется двойным интегралом от функции f(x, y) по области D.

Если областью интегрирования является окружность или часть окружности, то двойной интеграл проще вычислить в полярных координатах. Обобщением понятия двойного интеграла для функции трёх переменных является тройной интеграл.

Видео:Как расставить пределы интегрирования в двойном интегралеСкачать

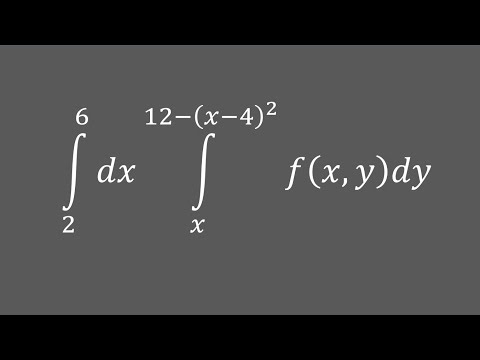
Двойной интеграл по треугольнику

Пусть область интегрирования (R) типа (I) (элементарная относительно оси (Oy)) ограничена графиками функций (x = a,) (x = b,) (y = pleft( x
ight)) и (y = qleft( x
ight).) При этом выполняются неравенства (a lt b) и (pleft( x
ight) lt qleft( x
ight)) для всех (x in left[
ight].) Тогда двойной интеграл по области (R) выражается через повторный по формуле [ > = ^ ^
ight)dydx> > .> ] Аналогичное соотношение существует и для области типа (II.) Пусть область интегрирования (R) типа (II) (элементарная относительно оси (Ox)) ограничена графиками функций (x = uleft( y
ight),) (x = vleft( y
ight),) (y = c,) (y = d) при условии, что (c lt d) и (uleft( y
ight) lt vleft( y
ight)) для всех (y in left[
ight].) Тогда двойной интеграл, заданный в области (R,) выражается через повторный интеграл по формуле [ > = ^ ^
ight)dxdy> > .> ] При решении задач иногда полезно разбить исходную область интегрирования (R) на две или более областей и вычислять двойной интеграл в каждой области отдельно.

Геометрические приложения двойного интеграла

Пример. Вычислить двойной интеграл по области D, где D – треугольник с вершинами в точках О(0,0), А(1,1) и В(0,2).

Решение. Построим область D и запишем уравнения линий, ограничивающих эту область (рис. 7).

Уравнение ОА: ; отрезок ВА задается уравнением ; OB – .

Пример. Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением .

Решение. Произведем замену переменных, полагая . Тогда уравнение кривой примет вид

Тогда . С учетом того, что имеет период T = , .

С учетом симметрии фигуры вычислим площадь четвертой части и результат умножим на четыре.

Вычислим площадь по формуле .

Площадь всей фигуры, ограниченной данной линией, .

Функции, не являющиеся ни чётными, ни нечётными, принято называть функциями общего вида.

Любую функцию, область определения которой симметрична относительно точки x = 0, можно единственным образом представить в виде суммы чётной и нечётной.

Опр. 4.1.15. Функция называется периодической, если существует число Т ¹ 0 такое, что для » x Î X: 1. x+Т Î X; 2. f(x+Т) = f(x). Число Т называется периодом функции.

Периодическими являются тригонометрические функции. Нетривиальные примеры: периодична любая постоянная функция f(x) = С=const; периодична функция Дирихле, причем её периодом может служить любое рациональное число. Из определения следует, что если Т – период функции, то числа 2Т, 3Т, …. – тоже периоды. Наименьший отличный от нуля положительный период называется основным периодом. Функция Дирихле демонстрирует пример периодической функции, не имеющей основного периода.