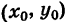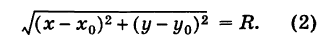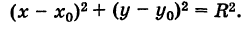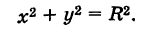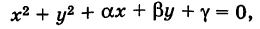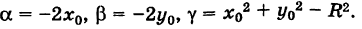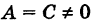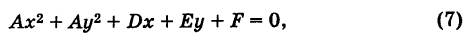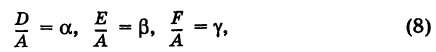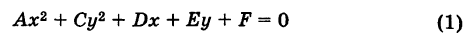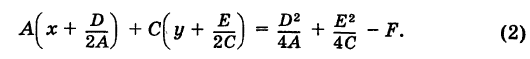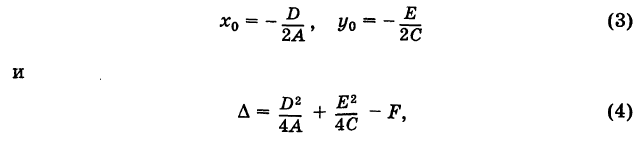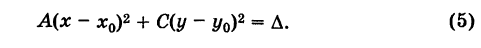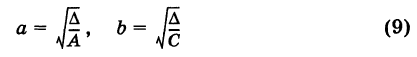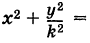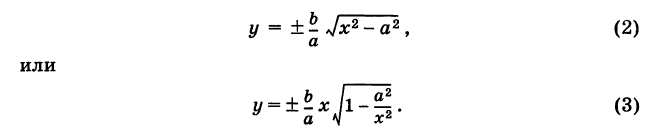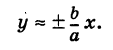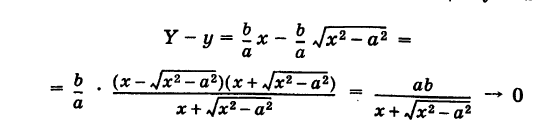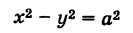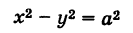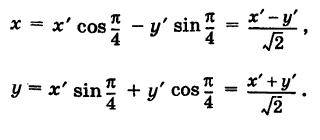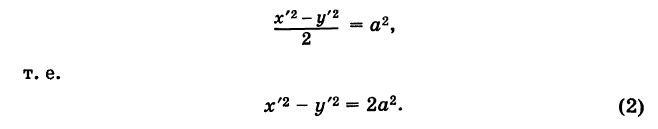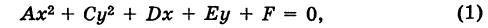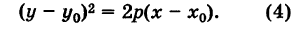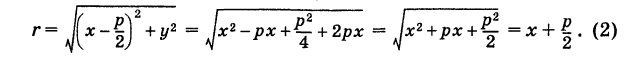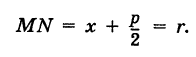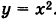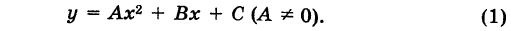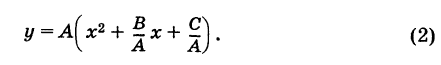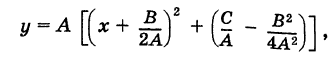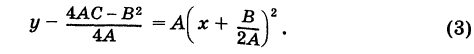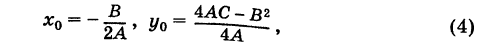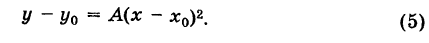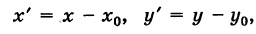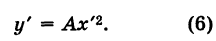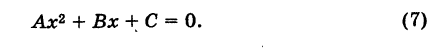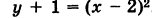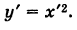График окружности с минусом (6 видео) | Курс школьной геометрии

Арккосинус. Решение уравнения cos x=a

Содержание

п.1. Понятие арккосинуса
п.2. График и свойства функции y=arccosx
п.3. Уравнение cos⁡x=a
п.4. Формула арккосинуса отрицательного аргумента
п.5. Примеры
Уравнение окружности.
Линии второго порядка — определение и вычисление с примерами решения
Линии второго порядка
Окружность
Центральные кривые второго порядка
Асимптоты гиперболы
График обратной пропорциональности
Нецентральные кривые второго порядка
Фокальное свойство параболы
График квадратного трехчлена
📸 Видео

п.1. Понятие арккосинуса

В записи (y=cosx) аргумент x — это значение угла (в градусах или радианах), функция y – косинус угла, действительное число в пределах [-1;1]. Т.е., по заданному углу мы находим косинус.
Можно поставить обратную задачу: по заданному косинусу найти угол. Но одному значению косинуса соответствует бесконечное количество углов. Например, если (cosx=1), то (x=2pi k, kinmathbb); (cosx=0), то (x=fracpi2+pi k, kinmathbb) и т.д.
Поэтому, чтобы построить однозначную обратную функцию, ограничим значения углов x отрезком, на котором косинус принимает все значения из [-1;1], но только один раз: (0leq xleq pi) (верхняя половина числовой окружности).

(arccosfrac12=fracpi3, arccosleft(-frac<sqrt>right)=frac)
(arccos2) – не существует, т.к. 2> 1

п.2. График и свойства функции y=arccosx

1. Область определения (-1leq xleq1) .
2. Функция ограничена сверху и снизу (0leq arccosxleq pi) . Область значений (yin[0;pi])
3. Максимальное значение (y_=pi) достигается в точке x =-1
Минимальное значение (y_=0) достигается в точке x =1
4. Функция убывает на области определения.
5. Функция непрерывна на области определения.

п.3. Уравнение cos⁡x=a

Значениями арккосинуса могут быть только углы от 0 до π (180°). А как выразить другие углы через арккосинус?

Углы в нижней части числовой окружности записывают через отрицательный арккосинус. А углы, которые превышают π по модулю, записывают через сумму арккосинуса и величины, которая ‘не помещается» в область значений арккосинуса.

1) Решим уравнение (cosx=frac12).
Найдем точку (frac12) в числовой окружности на оси косинусов (ось OX). Построим вертикаль – перпендикуляр, проходящий через точку. Он пересечёт числовую окружность в двух точках, соответствующих углам (pmfracpi3) — это базовые корни.
Если взять верхний корень (fracpi3) и прибавить к нему полный оборот (fracpi3+2pi=frac), косинус полученного угла (cosfrac=frac12), т.е. (frac) также является корнем уравнения. Корнями будут и все другие углы вида (fracpi3+2pi k) (с любым количеством добавленных или вычтенных полных оборотов). Аналогично, корнями будут все углы вида (-fracpi3+2pi k).
Получаем ответ: (x=pmfracpi3+2pi k)

Заметим, что полученный ответ является записью вида
(x=pm arccosfrac12+2pi k)
А т.к. арккосинус для (frac12) точно известен и равен (fracpi3), то мы его и пишем в ответе.
Но так бывает далеко не всегда.

2) Решим уравнение (cosx=0,8)

Найдем точку 0,8 в числовой окружности на оси косинусов (ось OX). Построим вертикаль – перпендикуляр, проходящий через точку. Он пересечёт числовую окружность в двух точках.
По определению верхняя точка – это угол, равный arccos⁡0,8.
Тогда нижняя точка – это тот же угол, но отложенный в отрицательном направлении обхода числовой окружности, т.е. (–arccos⁡0,8).
Добавление или вычитание полных оборотов к каждому из решений даст другие корни.
Получаем ответ:
(x=pm arccos0,8+2pi k)

п.4. Формула арккосинуса отрицательного аргумента

Докажем полезную на практике формулу для (arccos(-a)).

По построению: $$ begin angle DA’O=angle BAO=angle CAO=90^\ OD=OB=OC=1\ OA’=OA=a end Rightarrow $$ (по катету и гипотенузе) begin Delta DA’O=Delta BAO=Delta CAORightarrow\ Rightarrow angle DOC=angle A’OA-alpha+alpha=angle A’OA=180^=pi\ -arccosa+pi=arccos(-a) end

п.5. Примеры

Пример 1. Найдите функцию, обратную арккосинусу. Постройте графики арккосинуса и найденной функции в одной системе координат.

Для (y=arccosx) область определения (-1leq xleq 1), область значений (0leq yleq pi).
Обратная функция (y=cosx) должна иметь ограниченную область определения (0leq xleq pi) и область значений (-1leq yleq 1).
Строим графики:

Графики симметричны относительно прямой y=x.
Обратная функция найдена верно.

Пример 2. Решите уравнения:

a) (cos x=-1) (x=pi+2pi k)	б) (cos x=frac<sqrt>) (x=pmfracpi4+2pi k)
в) (cos x=0) (x=pmfracpi2+2pi k=fracpi2+pi k)	г) (cos x=sqrt) (sqrtgt 1, xinvarnothing) Решений нет
д) (cos x=0,7) (x=pm arccos(0,7)+2pi k)	e) (cos x=-0,2) (x=pm arccos(-0,2)+2pi k)

Пример 3. Запишите в порядке возрастания: $$ arccos0,8; arccos(-0,5); arccosfracpi7 $$

Способ 1. Решение с помощью числовой окружности

Отмечаем на оси косинусов (ось OX) точки с абсциссами 0,8; -0,5; (fracpi7approx 0,45)
Значения арккосинусов (углы) считываются на верхней половине окружности: чем меньше косинус (от 1 до -1), тем больше угол (от 0 до π).
Получаем: (angle A_1OAltangle A_2OAangle A_3OA)
$$ arccos0,8lt arccosfracpi7lt arccos(-0,5) $$Способ 2. Решение с помощью графика (y=arccosx)

Отмечаем на оси OX аргументы 0,8; -0,5; (fracpi7approx 0,45). Восстанавливаем перпендикуляры на кривую, отмечаем точки пересечения. Из точек пересечения с кривой восстанавливаем перпендикуляры на ось OY — получаем значения арккосинусов по возрастанию: $$ arccos0,8lt arccosfracpi7lt arccos(-0,5) $$Способ 3. Аналитический
Арккосинус – функция убывающая: чем больше аргумент, тем меньше функция.
Поэтому располагаем данные в условии аргументы по убыванию: 0,8; (fracpi7); -0,5.
И записываем арккосинусы по возрастанию: (arccos0,8lt arccosfracpi7lt arccos(-0,5))

Пример 4*. Решите уравнения:
(a) arccos(x^2-3x+3)=0) begin x^2-3x+3=cos0=1\ x^2-3x+2=0\ (x-2)(x-1)=0\ x_1=1, x_2=2 end Ответ:

(б) arccos^2x-arccosx-6=0)
( text -1leq xleq 1 )
Замена переменных: (t=arccos x, 0leq tleq pi)
Решаем квадратное уравнение: $$ t^2-t-6=0Rightarrow (t-3)(t+2)=0Rightarrow left[ begin t_1=3\ t_2=-2lt 0 — text end right. $$ Возвращаемся к исходной переменной: begin arccosx=3\ x=cos3 end Ответ: cos3

(в) arccos^2x-pi arccosx+frac=0)
( text -1leq xleq 1 )
Замена переменных: (t=arccos x, 0leq tleq pi)
Решаем квадратное уравнение: begin t^2-pi t+frac=0\ D=(pi^2)-4cdot frac=frac, sqrt=fracpi3\ left[ begin t_1=frac=fracpi3\ t_2=frac=frac end right. Rightarrow left[ begin arccosx_1=fracpi3\ arccosx_2=frac end right. Rightarrow left[ begin x_1=cosleft(fracpi3right)=frac12\ x_2=cosleft(fracright)=-frac12 end right. end Ответ: (left)

Видео:Уравнение окружности (1)Скачать

Уравнение окружности.

Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.

В формулировке окружности упоминается расстояние между точкой окружности и центром.

Формула расстояния между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) имеет вид:

Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х₀; у₀) и радиусом r.

Отметим произвольную точку М(х; у) на этой окружности.

Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.

Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х₀ ) 2 +(у – у₀ ) 2 = r 2 .

Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х₀; у₀) и радиусом r имеет вид:

В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):

Видео:Уравнение окружности. Как построить график уравнения окружности?Скачать

Линии второго порядка — определение и вычисление с примерами решения

Содержание:

Видео:График окружности за минуту #математика #егэ2023 #школа #егэ #fyp #shortsСкачать

Линии второго порядка

Окружность

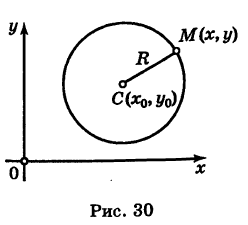
Выведем уравнение окружности (рис. 30) с центром С

Отсюда, вспоминая формулу расстояния между двумя точками, имеем

Так как обе части равенства (2) положительны, то, возводя в квадрат, получим равносильное уравнение

Итак, координаты любой точки М (х, у) данной окружности удовлетворяют уравнению (3). Справедливо также обратное утверждение.

Таким образом, уравнение (3) представляет собой уравнение окружности радиуса R с центром в точке С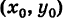. Это уравнение назвают нормальным уравнением окружности.

В частности, полагая х0 = 0 и у0 = 0, получим уравнение окружности с центром в начале координат

Уравнение окружности (3) после несложных преобразований можно привести к виду

где

Таким образом, окружность является кривой второго порядка.

Сравнивая уравнение (5) с общим уравнением кривой второго порядка

(6)

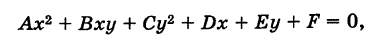
мы видим, что в (5) В = 0 и, кроме того, А — 1, С = 1, т. е. А = С. Обратно, положим в (6) В = 0 и

Деля уравнение (7) почленно на 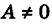и полагая

мы приходим к уравнению вида (5).

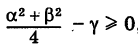
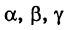
Уравнение (7) называется общим уравнением окружности. Заметим, однако, что не всякое уравнение (7) является уравнением действительной окружности. Легко показать, что (7) определяет действительную кривую (окружность) лишь при где выражаются равенствами (8).

Таким образом, действительная кривая второго порядка является окружностью тогда и только тогда, когда: 1) коэффициенты при квадратных текущих координат равны между собой и 2) отсутствует член, содержащий произведение текущих координат.

Центральные кривые второго порядка

Рассмотрим уравнение второго порядка

без члена с произведением координат х и у (В = О)1. Дополняя члены, содержащие x и у соответственно, до полных квадратов, будем иметь

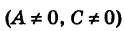
В нашем кратком курсе при рассмотрении общих уравнений кривых второго порядка мы ограничимся лишь этим случаем.

Отсюда, полагая

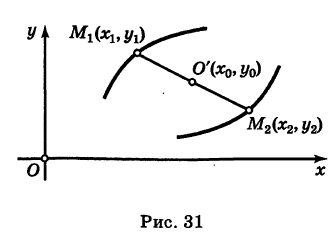
Точка О'(х0, у0) представляет собой центр симметрии кривой (5) (центр кривой). Действительно, если точка Мх(х19 У) лежит на кривой (5), то симметричная ей относительно О’ точка М2(х2, у2) где 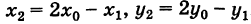— очевидно, также лежит на кривой (5) (рис. 31).

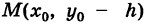
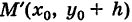
Параллельные осям координат Ох и Оу прямые у = у₀ и х = х₀ являются осями симметрии кривой (5) (оси кривой). Действительно, если точка лежит на кривой (5), то симметричная ей относительно прямой у = у0 точка также лежит на этой кривой. Аналогичным свойством обладает прямая х = х0.

В дальнейшем, для простоты исследования, будем предполагать, что центр кривой находится в начале координат, т. е. х₀ = О, 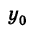= 0. Тогда уравнение кривой примет вид

Определение: Кривая второго порядка (6) называется эллипсом (точнее, принадлежит эллиптическому шипу)у если коэффициенты А и С имеют одинаковые знаки, т. е.

Для определенности будем полагать, что А > 0 и С > 0 (так как в противном случае знаки членов уравнения (6) можно изменить на обратные).

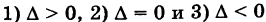
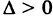
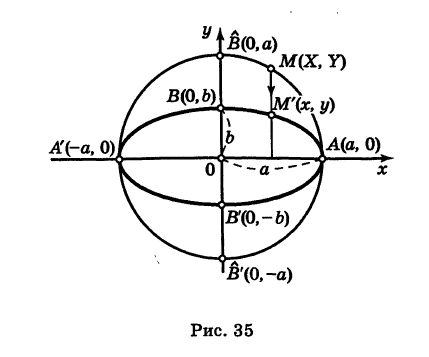
Возможны три случая: . В первом случае, , имеем действительный эллипс

где числа

называются полуосями эллипса. Обычно полагают 0 О, тогда С 0), а знак минус — левой ветви (х 1 — равномерное растяжение окружности.

Предположим, что при нашей деформации точка окружности М(Х, У) переходит в некоторую точку М(х, у) преобразованной кривой (рис. 35). Так как точки М и М’ лежат на одной и той же вертикали, то имеем

Отсюда при 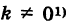получим

Подставляя эти выражения в уравнение (1), находим 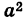, или

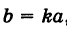
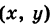
где т. е. преобразованная точка М’ расположена на эллипсе с полуосями а и Ь.

Обратно, если точка М’ 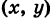принадлежит эллипсу (4), то соответствующая ей в силу (2) точка М(Х, У) лежит на окружности (1).

Таким образом, результат равномерной деформации окружности вдоль одного из ее диаметров представляет собой эллипс.

Асимптоты гиперболы

Рассмотрим гиперболу (см. рис. 33)

Решая уравнение (1) относительно у, получаем

Если х неограниченно возрастает, то 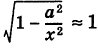и, следовательно, в некотором смысле, имеет место приближенное равенство

Покажем, что ветви гиперболы (1) сколь угодно близко подходят к прямым (см. рис. 33)

носящим название асимптот гиперболы. Действительно, например, при х > О возьмем в формулах (2) и (4) знаки плюс. Рассмотрим соответствующие точки М (х, у) гиперболы (2) и N (х, У) прямой (4), имеющие одну и ту же абсциссу х. Тогда

при

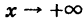
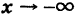
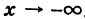
Аналогично рассматриваются еще три случая: знаки минус в (2) и в (4) при ; в (2) знак плюс, в (4) минус при и, наконец, в (2) минус, в (4) плюс при . Заметим, что сопряженная гипербола

как нетрудно проверить, имеет общие асимптоты с гиперболой (1).

Для равнобочной гиперболы (а = Ь)

ее асимптоты у = ±х взаимно перпендикулярны.

График обратной пропорциональности

Рассмотрим кривую (рис. 36)

Выбирая за новые оси координат Ох’ и Оу’ биссектрисы координатных углов и учитывая, что угол поворота будем иметь

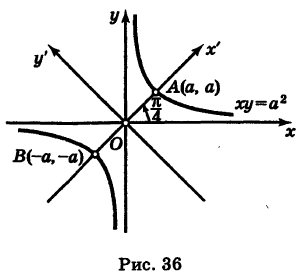
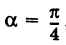
Отсюда на основании (1) получаем

Таким образом, графиком обратной пропорциональности (1) является равнобочная гипербола.

Нецентральные кривые второго порядка

Кривая второго порядка называется нецентральной, если она или не имеет центра симметрии, или же имеет бесконечно много центров симметрии (т. е. не имеет единственного центра). Рассмотрим кривую второго порядка

где 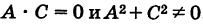. Для определенности будем считать, что

Кроме того, предположим, что 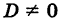, в противном случае мы бы имели пару параллельных прямых.

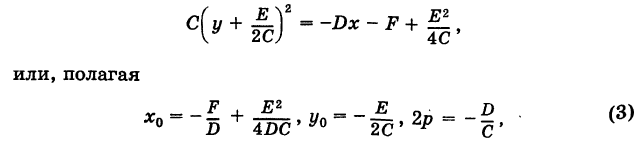
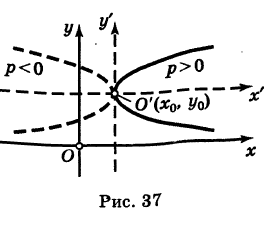
Дополняя в уравнении (1) члены с у до полного квадрата, будем иметь получим

Кривая (4) называется параболой (рис. 37); точка О’ (х0, у0) носит название вершины параболы у а число р называется параметром параболы. Легко убедиться, что прямая у = Уо является осью симметрии параболы (ось параболы); центра симметрии парабола (4) не имеет.

Если вершина параболы находится в начале координат, а ее осью является ось Ох, то мы получаем так называемое каноническое уравнение параболы причем параметр р здесь обычно считается положительным (этого можно добиться, выбирая надлежащее направление оси Ох; рис. 38, а).

Заметим, что если поменять ролями оси Ох и Оу, то каноническое уравнение параболы примет вид

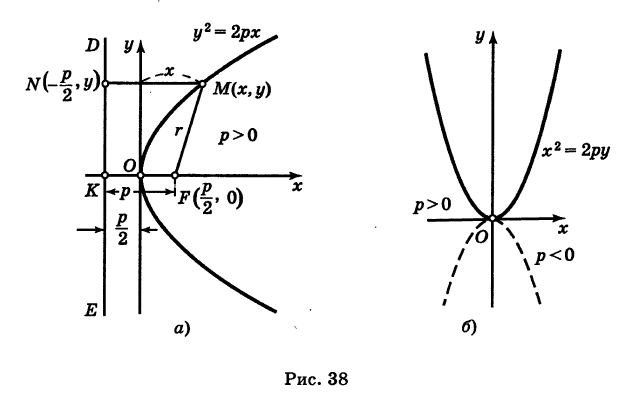
Это уравнение параболы с вертикальной осью (рис. 38, б).

Фокальное свойство параболы

Рассмотрим параболу (рис. 38, а)

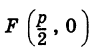
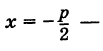
Точка называется ее фокусом, а прямая директрисой.

Для точки М(х, у) ее фокальный радиус г = MF равен

Далее, расстояние от этой точки до директрисы равно

Таким образом, парабола представляет собой множество всех точек плоскости, равноотстоящих от данной точки (фокуса) и от данной прямой (директрисы). Это характеристическое свойство параболы.

Пример:

Определить координаты фокуса и уравнение директрисы параболы

Решение:

Сравнивая это уравнение с уравнением (6), получим 2р = 1; отсюда р = 1/2. Следовательно, фокус параболы имеет координаты (0, 1/4), а уравнение директрисы есть у = -1/4.

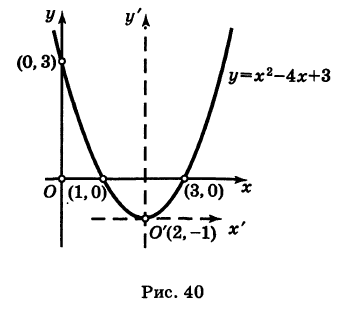
График квадратного трехчлена

Рассмотрим квадратный трехчлен

Дополняя выражение, стоящее в скобках, до полного квадрата, получим

то из формулы (3) получим

Делая параллельный перенос системы координат

окончательно будем иметь

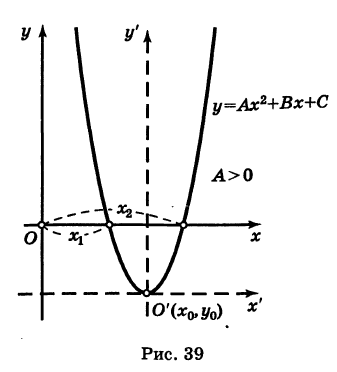
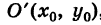
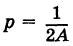
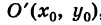
Уравнение (6) , формула (6) представляет собой каноническое уравнение параболы с вертикальной осью, вершина которой находится в точке и параметр . Таким образом, график квадратного трехчлена является параболой с вершиной в точке , ось которой параллельна оси Оу (парабола со смещенной вертикальной осью; рис. 39).

Заметим, что абсциссы 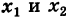точек пересечения параболы (1) с осью Ох являются корнями квадратного уравнения

На этом свойстве основан графический способ решения квадратного уравнения (7).

Пример:

Привести уравнение 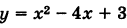к каноническому виду и построить соответствующую параболу.

Решение:

Перенося свободный член в левую часть уравнения и дополняя правую часть до полного квадрата, будем иметь у — 3 + 4 = = х2- 4х + 4, или

Полагая х-2=х’,у + 1 = у’, получим

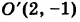
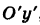
Таким образом, заданное уравнение есть уравнение параболы с вершиной в точке и осью симметрии параллельной оси Оу (рис. 40).

Рекомендую подробно изучить предметы:

Математика
Алгебра
Линейная алгебра
Векторная алгебра
Высшая математика
Дискретная математика
Математический анализ
Математическая логика

Ещё лекции с примерами решения и объяснением:

Полярные координаты
Непрерывность функции
Уравнения поверхности и линии в пространстве
Общее уравнение плоскости
Интегрирование тригонометрических функций
Интегрирование тригонометрических выражений
Интегрирование иррациональных функций
Прямоугольная система координат на плоскости и ее применение

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.