Главные центральные оси треугольника

6.6. ГЛАВНЫЕ ОСИ ИНЕРЦИИ И ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ

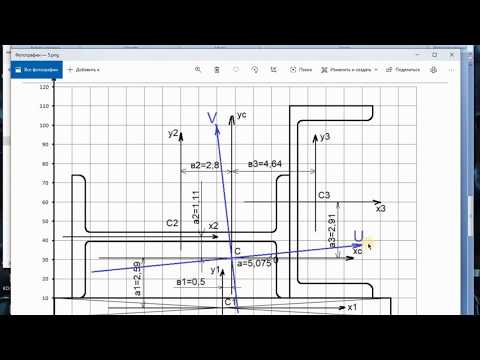
При изменении угла α значения Iz1, Iy1, Iz1y1 (6.13) изменяются, и при некотором значении угла α0 они принимают экстремальные значения. Взяв первую производную по углу α от формул (6.13) и приравняв ее нулю, получим: Эта формула определяет положение двух осей, относительно одной из которых осевой момент максимален, а относительно другой – минимален. Такие оси называют главными. Моменты инерции относительно главных осей называют главными моментами инерции. Их вычисляют следующим образом: Главные оси обладают следующими свойствами: центробежный момент инерции относительно них равен нулю; моменты инерции относительно главных осей экстремальны; для симметричных сечений оси симметрии являются главными. Главные оси, проходящие через центр тяжести фигуры, называют главными центральными осями инерции. Пример 6.4. Определить, каким образом изменяется момент инерции квадратного сечения при его повороте. Решение. Момент инерции относительно повернутой оси: Поскольку оси z, y квадрата являются осями симметрии, то есть главными, то центробежный момент инерции относительно них Izy = 0: Выводы. 1. Моменты инерции квадратного сечения с изменением положения центральных осей остаются постоянными. 2. В квадрате и других правильных многоугольниках (треугольниках, пятиугольниках) любая центральная ось является и главной. Такие фигуры называют фигурами равного сопротивления. Пример 6.5. Для фигуры, представленной в примере 6.1, определить главные центральные моменты инерции. Решение. Расстояния между центральной осью составной фигуры и собственными центральными осями элементов Моменты инерции относительно центральных осей, параллельных основанию и высоте a1= y1 – yC = 5 – 3,5 = 1,5 см; a2= y2 – yC = 1 – 3,5 = –2,5 см; b1= z1 – zC = 1 – 2,5 = –1,5 см; b2= z2 – zC = 5 – 2,5 = 2,5 см. Центробежный момент инерции Направления главных осей инерции Угол α0 (положительный) откладываем против хода часовой стрелки от оси с большим моментом инерции, то есть zC . Величины главных центральных моментов инерции

Видео:Геометрические характеристики. Моменты инерции. Радиусы инерции. Сопромат.Скачать

ПроСопромат.ру

Видео:Моменты инерции относительно Главных Центральных осей для простых фигурСкачать

Технический портал, посвященный Сопромату и истории его создания

Видео:Моменты инерции простейших фигур. Оси центральные и главные. Что это и где. #сопроматСкачать

Вопрос о главных центральных осях инерции сечения

Какие оси называются главными центральными, какими свойствами они обладают?

Центральные оси — это оси, проходящие через центр тяжести сечения. Относительно центральных осей статический момент площади сечения равен 0.

Главные оси — это оси, относительно которых центробежный момент инерции равен 0. Если главные оси проходят через центр тяжести сечения, то они являются главными центральными осями.

Если фигура симметрична относительно одной из осей, то эта ось симметрии является главной центральной осью, а вторая главная ось представляет собой перпендикуляр к этой оси.

Видео:Сопротивление материалов. Лекция: геометрические характеристики сечений - моменты инерцииСкачать

Момент инерции сечения

Меня часто спрашивают: «…а что такое моменты инерции в сопротивлении материалов и зачем они вообще?» Об этом в сегодняшней теме

Видео:Моменты инерции для треугольника. Вывод моментов инерции для треугольниковСкачать

Моменты инерции сечения из простых фигур

Начнем с моментов инерции простых фигур и на их примере выясним для сложных фигур и составных сечений из стандартных профилей.

Начать объяснение о том, что такое моменты инерции нужно с того, что спросить, а что такое площадь?

Обычная площадь квартиры, огорода сечения стержня? Зачем она и почему?

Так вот площадь это характеристика которую придумали и вывели для разных фигур, чтобы была возможность сравнивать земельные наделы. Не всегда они были прямоугольные или квадратные. А сравнить кто сколько получил в надел было нужно. Вот и вывели такую закономерность для прямоугольника, что если перемножить стороны — получим величину, которую можно будет сравнить с перемноженной высотой на основание деленное пополам для треугольника или для круга Пи умножить на эр в квадрате )). Т.е. площади простых фигур

Что касается моментов инерции в сопротивлении материалов, то тут они появились, когда стало понятно, что есть какая то геометрически измеримая величина для разных форм сечения, которая позволит сравнить сопротивляемость этих сечений изгибу.

Проще говоря бревно, которое выполняет роль балки и изгибается может иметь форму прямоугольника, квадрата или круга, а нам нужно сравнить их сопротивляемость изгибу. Вот для этих целей выводили формулу напряжений и оказалось, что в числителе оказался изгибающий момент, а в знаменателе момент инерции:

на балке изображены главные центральные оси z y

прогибы для таких балок будут разными относительно осей z и y, т.к. моменты инерции будут разные.

Видео:Моменты инерции относительно Главных Центральных осей для составной фигурыСкачать

Вывод моментов инерции для простых фигур

Так вот ниже я приведу видео уроки, плейлист, в котором один за одним выведены моменты инерции для простых фигур, а именно для прямоугольника, треугольника и круга. А затем приводится стандартный расчет моментов инерции для более сложной фигуры, которая состоит из нескольких простых. Всегда сложную фигуру можно разбить на несколько простых. Исходя из этого расчет и ведется.

Моменты инерции измеряются в единицах длины в 4 степени, т.е. см⁴ или м⁴. Чаще всего используется см⁴, т.к. такие единицы измерения приведены в сортаменте прокатной стали.

Момент инерции, это величина, которая показывает сопротивляемость сечения изгибу. На примере линейки хорошо понятно что изгиб в одной плоскости и изгиб в другой плоскости будут сильно отличаться, хотя площадь сечения не меняется. Вот это и было выведено в формуле для напряжений и для прогибов. Что величина, которая сопротивляется изгибающему моменту есть интеграл до координаты центра тяжести площадки в квадрате на площадь элементарной площадки.

Центральными осями называют оси, которые проходят через центр тяжести сечения

Главные оси располагаются в сечении таким образом, что центробежный момент относительно них равен нулю. Т.е. это максимальный и минимальный осевые моменты инерции

Оси, которые проходят через центр тяжести сечения и центробежный момент инерции относительно них равен нулю. При этом данные осевые моменты инерции являются экстремальными, т.е. имеют максимальное и минимальное значение. Именно относительно этих осей ведут расчет и к ним приводят нагрузки. Т.е. если какое нибудь внешнее усилие проходит в стороне от главных центральных осей. Это усилие переносят соблюдая правила переноса к главным центральным осям. Только после этого рассматривают действие сил и находят внутренние усилия относительно главных центральных осей инерции.

При вычислении моментов инерции осевых, при переходе от одних осей к другим появляется центробежный момент инерции, как составляющая пары осевых моментов инерции. И только для главных осей центробежные моменты инерции равны нулю. Именно эти оси мы и отыскиваем в наших расчетах. Поэтому мы ищем величину центробежного момента инерции для не главных осей и из свойства, что главные центральные оси это такие оси, относительно которых центробежный момент инерции равен нулю, находим положение главных центральных осей.

Видео:Определение положения главных центральных осей и главных центральных моментов инерцииСкачать

Моменты инерции для прямоугольника

Видео:Центральная симметрия. 6 класс.Скачать

#Сопромат, Моменты инерции. Прямоугольник. Вывод моментов инерции для прямоугольника.

Сопротивление материалов и Моменты инерции для прямоугольника. Понятие моментов инерции, формулы и вывод для прямоугольника. Осевые центробежный моменты инерции. для треугольника вывод моментов инерции в этом видео: https://www.youtube.com/embed/_pixohVoc-4?vq=hd720 Тема моментов инерции возникла в связи стем, что для определения напряжений при изгибе понадобилась геометрическая характеристика, которая сопротивляется внутреннему усилию (изгибающему моменту). В результате вывода формулы напряжений и появилась эта формула, выраженная через интеграл от квадрата координаты помноженной на площадь элементарной площадки. Эту геометрическую характеристику и назвали моментом инерции. пройти полный курс обучения сопромату и строймеху онлайн, по скайпу. Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline

2018-04-09

моменты инерции для прямоугольника для главных центральных осей равны, формула

моменты инерции для прямоугольника для осей проходящих через основные размеры равны, формула

Моменты инерции для треугольника

Видео:8 класс, 9 урок, Осевая и центральная симметрияСкачать

Сопротивление материалов, Моменты инерции для треугольника. Сопромат вывод моментов инерции

Сопротивление материалов и Моменты инерции для треугольника. Сопромат вывод моментов инерции для простых фигур. Моменты инерции для треугольника. Моменты инерции для осей в треугольнике, которые проходят через основные размеры. Вывод и пояснение к этой теме сопротивления материалов. для прямоугольника вывод моментов инерции в этом видео: https://www.youtube.com/watch?v=v1TE1UW_sRE&feature=youtu.be‎ Тема моментов инерции возникла в связи стем, что для определения напряжений при изгибе понадобилась геометрическая характеристика, которая сопротивляется внутреннему усилию (изгибающему моменту). В результате вывода формулы напряжений и появилась эта формула, выраженная через интеграл от квадрата координаты помноженной на площадь элементарной площадки. Эту геометрическую характеристику и назвали моментом инерции. пройти полный курс обучения сопромату и строймеху онлайн, по скайпу Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline

2018-04-09

Моменты инерции треугольника относительно произвольых осей

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Момент инерции круга. Моменты инерции простых фигур. #сопромат

Вывод моментов инерции для круга. Видео урок из темы «Моменты инерции простых фигур». В видео приведен вывод момента инерции полярного, в полярной системе координат Ip Затем выведены моменты инерции осевые Iz, Iy. Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline

2019-09-14

Видео:Осевая симметрия. 6 класс.Скачать

Моменты инерции. Оси центральные и главные. Что это и где. #сопромат

Центральные оси — любая пара взаимно перпендикулярных осей, которые проходят через центр тяжести фигуры Главные оси — оси для которых центробежный момент инерции равен нулю, а осевые моменты имеют максимум и минимум. Об этом и многом другом в видео уроке по моментам инерции в сопротивлении материалов Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline

2019-09-14

Видео:Треугольник и окружность #shortsСкачать

Примеры расчетов моментов инерции для сечений

Ниже приводятся примеры расчетов моментов инерции относительно главных центральных осей, объяснение, что такое центробежный момент инерции и почему оси называются главными центральными для примеров:

• простейшие фигуры — прямоугольник, треугольник
• составные сечения из простейших треугольника и прямоугольника
• составные из прокатных профилей

Пример расчета моментов инерции относительно главных центральных осей для простейших фигур

Подробно объясняется как найти центробежный момент инерции, как найти осевые моменты инерции, как относительно центральных и как относительно главных осей для простых фигур.

Пример расчета моментов инерции для сечения состоящего из прямоугольника и треугольника

Сечения балок может быть составным, т.е. таким, которое складывается из нескольких фигур. В примере, в видеоуроке ниже рассказыватся как найти моменты инерции относительно главных центральных осей для такого сечения балки

Расчет моментов инерции сечения составного из стандартных прокатных профилей

В видеоуроке ниже разбирается порядок расчета моментов инерции относительно главных центральных осей для сечения составленого из трех прокатных профилей уголков

📸 Видео

6. Определение характеристик сечения ( практический курс по сопромату )Скачать

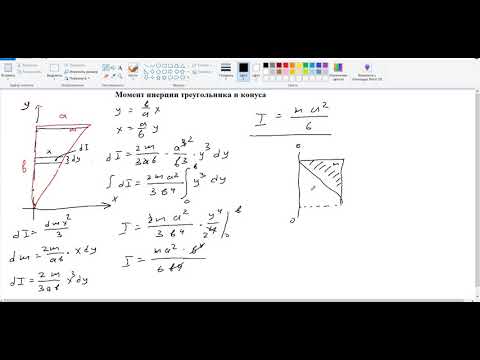
7. Момент инерции треугольника и конусаСкачать

Теория (часть 1) осевые моменты инерцииСкачать

Осевая и центральная симметрия, 6 классСкачать

Моменты инерции сечения из простых фигурСкачать

Определение центра тяжести сложной фигуры. СопроматСкачать

Вычисление моментов инерции составного сеченияСкачать