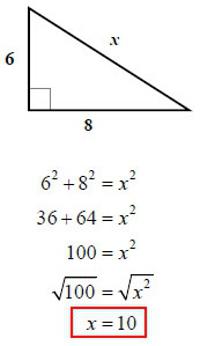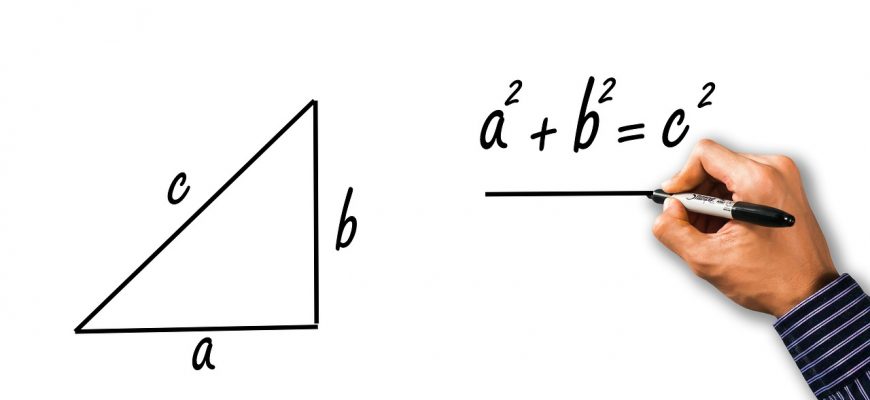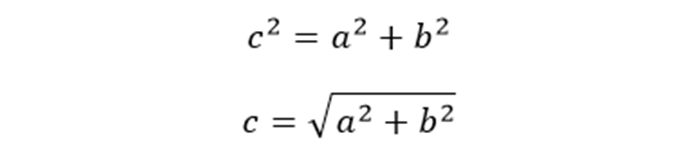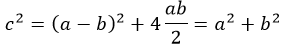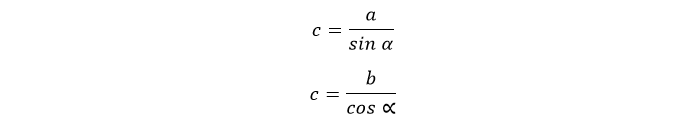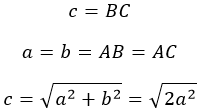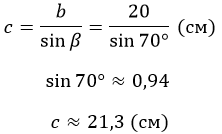Гипотенуза не прямоугольного треугольника

После изучения темы про прямоугольные треугольники ученики часто выбрасывают из головы всю информацию о них. В том числе и то, как найти гипотенузу, не говоря уже о том, что это такое.

И напрасно. Потому что в дальнейшем диагональ прямоугольника оказывается этой самой гипотенузой, и ее нужно найти. Или диаметр окружности совпадает с самой большой стороной треугольника, один из углов которого прямой. И найти ее без этого знания невозможно.

Существует несколько вариантов того, как найти гипотенузу треугольника. Выбор метода зависит от исходного набора данных в условии задачи величин.

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Способ под номером 1: даны оба катета

Это самый запоминающийся метод, потому что использует теорему Пифагора. Только иногда ученики забывают, что по этой формуле находится квадрат гипотенузы. Значит, чтобы найти саму сторону, нужно будет извлечь квадратный корень. Поэтому формула для гипотенузы, которую принято обозначать буквой «с», будет выглядеть так:

с = √ (а 2 + в 2 ), где буквами «а» и «в» записаны оба катета прямоугольного треугольника.

Видео:Теорема Пифагора для чайников)))Скачать

Способ под номером 2: известен катет и угол, который к нему прилежит

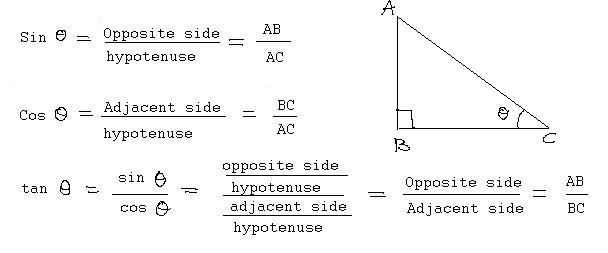
Для того чтобы узнать, как найти гипотенузу, потребуется вспомнить тригонометрические функции. А именно косинус. Для удобства будем считать, что даны катет «а» и прилежащий к нему угол α.

Теперь нужно вспомнить, что косинус угла прямоугольного треугольника равен отношению двух сторон. В числителе будет стоять значение катета, а в знаменателе — гипотенузы. Из этого следует, что последнюю можно будет сосчитать по формуле:

с = а / cos α.

Видео:Как найти гипотенузу в прямоугольном треугольнике, минуя теорему Пифагора?Скачать

Способ под номером 3: даны катет и угол, который лежит напротив него

Чтобы не запутаться в формулах, введем обозначение для этого угла — β, а сторону оставим прежнюю «а». В этом случае потребуется другая тригонометрическая функция — синус.

Как и в предыдущем примере, синус равен отношению катета к гипотенузе. Формула этого способа выглядит так:

с = а / sin β.

Для того чтобы не запутаться в тригонометрических функциях, можно запомнить простое мнемоническое привило: если в задаче идет речь о противолежащем угле, то нужно использовать синус, если — о прилежащем, то косинус. Следует обратить внимание на первые гласные в ключевых словах. Они образуют пары о-и или и-о.

Видео:Нахождение стороны прямоугольного треугольникаСкачать

Способ под номером 4: по радиусу описанной окружности

Теперь, для того чтобы узнать, как найти гипотенузу, потребуется вспомнить свойство окружности, которая описана около прямоугольного треугольника. Оно гласит следующее. Центр окружности совпадает с серединой гипотенузы. Если сказать по-другому, то самая большая сторона прямоугольного треугольника равна диагонали окружности. То есть удвоенному радиусу. Формула для этой задачи будет выглядеть так:

с = 2 * r, где буквой r обозначен известный радиус.

Это все возможные способы того, как находить гипотенузу прямоугольного треугольника. Пользоваться в каждой конкретной задаче нужно тем методом, который больше подходит по набору данных.

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Пример задачи №1

Условие: в прямоугольном треугольнике проведены медианы к обоим катетам. Длина той, которая проведена к большей стороне, равна √52. Другая медиана имеет длину √73. Требуется вычислить гипотенузу.

Так как в треугольнике проведены медианы, то они делят катеты на два равных отрезка. Для удобства рассуждений и поиска того, как найти гипотенузу, нужно ввести несколько обозначений. Пусть обе половинки большего катета будут обозначены буквой «х», а другого — «у».

Теперь нужно рассмотреть два прямоугольных треугольника, гипотенузами у которых являются известные медианы. Для них нужно дважды записать формулу теоремы Пифагора:

(2у) 2 + х 2 = (√52) 2

(у) 2 + (2х) 2 = (√73) 2 .

Эти два уравнения образуют систему с двумя неизвестными. Решив их, легко можно будет найти катеты исходного треугольника и по ним его гипотенузу.

Сначала нужно все возвести во вторую степень. Получается:

Из второго уравнения видно, что у 2 = 73 — 4х 2 . Это выражение нужно подставить в первое и вычислить «х»:

4(73 — 4х 2 ) + х 2 = 52.

292 — 16 х 2 + х 2 = 52 или 15х 2 = 240.

Из последнего выражения х = √16 = 4.

Теперь можно вычислить «у»:

у 2 = 73 — 4(4) 2 = 73 — 64 = 9.

По данным условия получается, что катеты исходного треугольника равны 6 и 8. Значит, можно воспользоваться формулой из первого способа и найти гипотенузу:

√(6 2 + 8 2 ) = √(36 + 64) = √100 = 10.

Ответ: гипотенуза равна 10.

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Пример задачи №2

Условие: вычислить диагональ, проведенную в прямоугольнике с меньшей стороной, равной 41. Если известно, что она делит угол на такие, которые соотносятся как 2 к 1.

В этой задаче диагональ прямоугольника является наибольшей стороной в треугольнике с углом 90º. Поэтому все сводится к тому, как найти гипотенузу.

В задаче идет речь об углах. Это значит, что нужно будет пользоваться одной из формул, в которых присутствуют тригонометрические функции. А сначала требуется определить величину одного из острых углов.

Пусть меньший из углов, о которых идет речь в условии, будет обозначен α. Тогда прямой угол, который делится диагональю, будет равен 3α. Математическая запись этого выглядит так:

Из этого уравнения просто определить α. Он будет равен 30º. Причем он будет лежать напротив меньшей стороны прямоугольника. Поэтому потребуется формула, описанная в способе №3.

Гипотенуза равна отношению катета к синусу противолежащего угла, то есть:

Видео:Катеты и гипотенузаСкачать

Гипотенуза треугольника

Гипотенуза треугольника — это такая сторона треугольника, длина которой равна
квадратному корню из суммы квадратов длин двух других сторон.

Можно сказать, что в треугольнике есть гипотенуза, если длину
какой-нибудь стороны можно выразить по формуле:

Это формула из Теоремы Пифагора. Где с — гипотенуза треугольника, a и b — катеты треугольника.

Не во всех треугольниках есть гипотенуза!

Признаки наличия гипотенузы в треугольнике

Существует ряд случаев / признаков по которым
можно определить, что в треугольнике есть гипотенуза:

• Прямоугольный треугольник;
• Треугольник, у которого один из углов прямой, по условию;
• Два угла треугольника по 45 градусов;
• Треугольник, к которому можно применить Теорему Пифагора;
• Если в треугольнике известны только два угла, и третий угол
  является прямым (по теореме о сумме углов треугольника);
• Квадратный корень из суммы квадратов длин двух
  сторон треугольника равен длине третьей стороне;
• По условию задачи две стороны являются катетами.
• Египетский треугольник;

Если хотя бы один из вышеперечисленных признаков верен,
соответствует условию задачи, то в треугольнике есть гипотенуза.

Пример гипотенузы в треугольнике

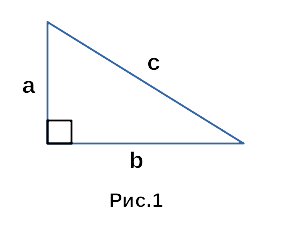
На рисунке 1 изображен прямоугольный треугольник со сторонами a, b, c.

В данном случае, определить какая сторона является гипотенузой
довольно таки просто. Стороны a и b образуют прямой угол,
поэтому сторона c — гипотенуза. Сторона c является гипотенузой
треугольника, так как два смежных с ней угла, образуют в
сумме угол в 90 градусов, т.е прямой.

Длина гипотенузы треугольника

Мы могли бы определить является ли сторона гипотенузой произвольного
треугольника, зная только величину длин всех сторон треугольника.

Как узнать есть ли гипотенуза? Какова её длина?

Допустим, длина стороны a = 3, b = 4, c = 5, тогда по Теореме Пифагора (по признаку гипотенузы в треугольнике):

Все сходится, следовательно гипотенуза в треугольнике есть, и её длина равна 5.
Если в вашем случае ответ не сходится, числа получились в
итоге разные, значит, однозначно гипотенузы в треугольнике нет!

Длину гипотенузы треугольника, можно узнать с помощью Теоремы Пифагора, только в трех базовых случаях:

1. В треугольнике известны длины двух сторон, есть прямой угол;
2. Два угла треугольника по 45 градусов, известна только одна сторона;
3. Известны длины всех сторон треугольника;

Видео:Определение длины гипотенузыСкачать

Гипотенуза — формула, правила и примеры вычислений

Слово «гипотенуза» со школьных времен у многих вызывает негативные ассоциации. Добавим загадочного и непонятного. Происходит от греческого «ὑποτείνουσα».

А ведь означает всего-навсего «вытянутый». И речь идет о простейшей форме треугольника – прямоугольной (рис. 1).

Гипотенузой называют сторону напротив прямого угла. Самую протяженную. В данном случае – с. Остальные составляющие – катеты.

Простыми фигурами интересовались древние строители Вавилона и Египта. А особенно – землемеры. Еще бы: ведь основа любой цивилизации – распределение угодий и налоги.

Считается, что теоретическая база была доказательно предложена Пифагором в V-м веке до н. э. Хотя, скорее всего, это было сделано ранее.

Видео:7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

Теорема Пифагора

Сумма квадратов катетов составляет квадрат гипотенузы:

Верно и обратное утверждение. Треугольник, удовлетворяющий приведенному равенству – прямоугольный.

Формула верна только в Евклидовой геометрии, где параллельные прямые не пересекаются.

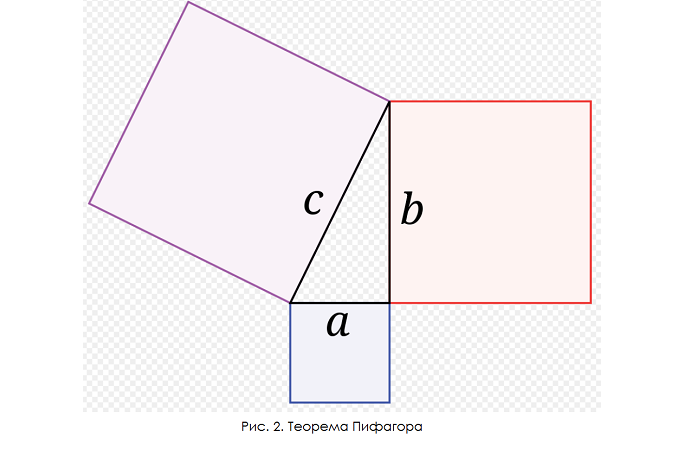
Утверждение приведено в современной интерпретации. В оригинале выглядит несколько по-другому: площадь квадрата, построенного на гипотенузе, идентична сумме площадей квадратов, построенных на катетах (рис. 2).

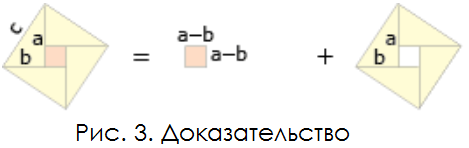
Существует масса способов доказательства. В том числе весьма сложных. А попадаются удивительно изящные, как например, на рисунке 3:

Видео:ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

В тригонометрии

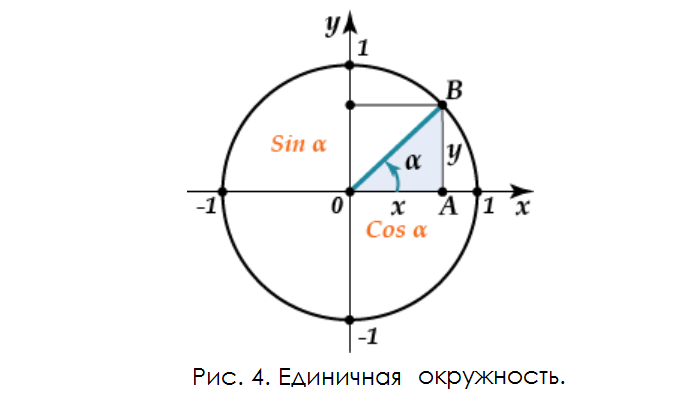
Построим на плоскости прямоугольную систему координат с единичной (с радиусом, равным 1) окружностью с центром в точке (0; 0). B – пересечение угла α и кривой (рис. 4).

На оси абсцисс X отмечается cos α; на оси ординат Y – sin α.

В получившемся прямоугольном треугольнике отрезок 0B является гипотенузой. Учитывая доказанную теорему, выводим основное равенство математической дисциплины:

sin 2 α + cos 2 α = 1

Видео:Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать

Гипотенуза прямоугольного треугольника

Связана со сторонами следующими соотношениями (см. рис. 1):

a – противолежащий α катет;

Величины sin α и cos α меньше либо равны 1, что очевидно из рис. 4. Но в треугольнике не может быть два прямых угла. Как не может быть нулевого.

Это означает, что гипотенуза – всегда наибольшая сторона треугольника, т. е.

Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

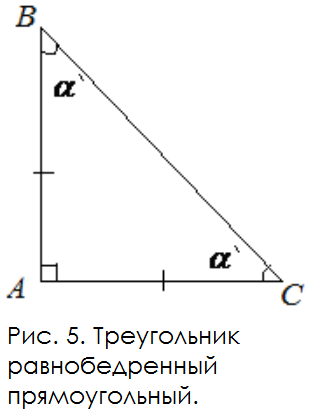
Гипотенуза равнобедренного треугольника

В такой фигуре катеты равны и являются сторонами прямого угла (рис. 5). Расчет гипотенузы c производится по формуле теоремы Пифагора.

Нетрудно заметить, что углы α = 45°. Поскольку сумма всех равна 180°.

Видео:Этой задачей русские дети 10 лет мучили американцев. Американцы не понимали, что делают не такСкачать

Пример решения задачи

Дан прямоугольный треугольник ABC (рис. 1). Рассчитайте длину AB, если b = 20 см, а β = 70°.

AC является катетом, противолежащим углу β. Значит нахождение гипотенузы сводится к отношениям:

Ответ: АВ = 21,3 см.

В интернете есть онлайн калькуляторы для оперативного расчета величины. Но целесообразно ими пользоваться разве что при значительном объеме вычислений. Ведь формулы довольно просты.

Связанные с упомянутыми фигурами задачи распространены в реальной жизни. Приведенные уравнения призваны помочь в решении.

📺 Видео

Площадь прямоугольного треугольника. Как найти площадь прямоугольного треугольника?Скачать

СЕРЬЁЗНО готовимся к ОГЭ 2024! / Полный прогон задания 17 на ОГЭ по математикеСкачать

Найдите углы прямоугольного треугольника, если его гипотенуза равна 12, а площадь равна 18Скачать

Советская олимпиада, которую сегодня решить только 2 школьниковСкачать

Свойства прямоугольного треугольника. 7 класс.Скачать

Геометрия Найдите катет прямоугольного треугольника, если его гипотенуза и второй катетСкачать

Найдите площадь прямоугольного треугольника, если сумма его катетов равна 15, а гипотенуза равна 13Скачать