Индивидуальный учебный проект по теме «Треугольники».
В работе рассматриваются основные типы и свойства треугольников, в том числе изучение которых не входит в школьную программу.
А также изучение сведений о нахождении треугольников в окружающем мире.
Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Скачать:
| Вложение | Размер |
|---|---|
| gyndya_a._treugolniki.docx | 803.48 КБ |
Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Предварительный просмотр:
Муниципальное образовательное учреждение
Дашковская средняя общеобразовательная школа
Итоговый проект по математике
за курс 9 класса
по теме: «Треугольники»
На протяжении всей своей сознательной жизни каждый человек проявляет неподдельный интерес к такой геометрической фигуре, как треугольник. Игра в пирамидки, складывание оригами, составление аппликации из цветной бумаги с помощью треугольных фигурок — все эти действия дают ребёнку первое представление о треугольниках. Треугольники существуют в природе, в архитектуре, в искусстве и в окружающей нас жизни.
Актуальность данного проекта определяется важностью умения видеть математику в мире, в котором мы живём, необходимостью добывать знания о треугольниках, а также применением полученных знаний в повседневной жизни.
Цель : Обобщение знаний о треугольниках, и их практическом применении.
- Изучение исторических сведений о треугольниках;
- Изучение сведений о нахождении треугольников в окружающем мире;
- Исследование свойств треугольников и применения этих свойств в решении практических задач.
Практическая значимость: данный материал способствует формированию представления о прикладных возможностях математики.
Треугольник как символ. Исторические сведения.
Треугольник является одной из первых геометрических фигур, которая стала использоваться в орнаментах древних народов.
В Древнем Египте он был прямоугольным и являлся воплощением триады духовной воли, любви и высшего разума человека. Вертикальная сторона египетского треугольника составляла три единицы длины, основание — четыре, а гипотенуза – пять.
На Древнем Востоке почитали треугольник как символ природы всего сущего. Треугольник с вершиной, соединенной с такой же геометрической фигурой, ацтеки использовали в качестве эмблемы временного цикла. В буддийской традиции два смыкающихся треугольника олицетворяют чистое пламя и Три Драгоценности Будды. Китайский символ восстановления изображается в виде треугольника с подвешенными к нему мечами.
У христиан — треугольник, образованный тремя пересекающимися окружностями, олицетворяет Троицу в единении и равенстве трех ее составляющих. Два соединенных вершинами вертикальных треугольника разделяют символизм песочных часов, олицетворяя неумолимо идущее время и смертность. Также песочные часы часто используются для обозначения благочестивого, тихого образа жизни, краткости человеческой жизни, а также применяются как атрибут отца-времени и порой даже смерти.
Начиная с ранних христиан треугольник был символом Святой Троицы. Равносторонний треугольник толковался как равенство и единая божественная сущность Бога Отца, Бога Сына и Духа Святого. Иногда этот символ составляли из трех переплетенных между собой рыб. Символ Троицы по католической традиции составлялся из трех малых треугольников, вписанных в один большой с кругами на вершинах. Три этих круга означают триединство, но каждый круг независим и совершенен сам по себе. Эта схема иллюстрировала принцип триединства и вместе с тем индивидуальности каждого составляющего Святой Троицы.
Печать Соломона — другое название звезды Давида, образованной наложением друг на друга двух треугольников, т.е. гексаграммы. По преданию, царь Соломон с помощью этого знака управлял духами, заключенными в медный сосуд. Считается, что печать Соломона является мощным амулетом, способным защитить своего обладателя от влияния злых духов.
Раздел II. Треугольник в геометрии.
Треугольник — это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки, образующие треугольник, называются вершинами треугольника.
Стороны треугольника образуют в вершинах треугольника три угла, поэтому треугольник можно также определить как многоугольник, у которого имеется ровно три угла. Треугольник является одной из важнейших геометрических фигур, повсеместно используемых в науке и технике, поэтому глубокое исследование его свойств проводилось начиная с глубокой древности.
2.1.1. Основные элементы треугольника ABC
Вершины – точки A, B, и C;
Стороны – отрезки a = BC, b = AC и c = AB, соединяющие вершины;
Углы – α, β, γ образованные тремя парами сторон. Углы часто обозначают так же, как и вершины, – буквами A, B и C.
Угол, образованный сторонами треугольника и лежащий в его внутренней области, называется внутренним углом, а смежный к нему является внешним углом треугольника.
2.1.2. Виды треугольников.
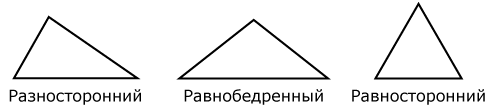
Треугольник называется разносторонним , если любые две стороны его не равны друг другу.
Треугольник, все стороны которого равны, называется равносторонним.
Треугольник называется равнобедренным , если у него две стороны равны.
Треугольник называется остроугольным , если все его углы острые.
Треугольник называется тупоугольным , если один из его углов тупой.
Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°.
Египетский треугольник –прямоугольный треугольник с соотношением сторон 3:4:5. Особенностью треугольника, известной ещё со времён античности, является то, что при таком отношении сторон теорема Пифагора даёт целые квадраты как катетов, так и гипотенузы, то есть 9:16:25.
Название треугольнику с таким отношением сторон дали эллины. В VII — V веках до н. э. греческие философы и общественные деятели активно посещали Египет. Так, например, Пифагор в 535 до н. э. по настоянию Фалеса для изучения астрономии и математики отправился в Египет — и, судя по всему, именно попытка обобщения отношения квадратов, характерного для египетского треугольника, на любые прямоугольные треугольники и привела Пифагора к формулировке и доказательству его знаменитой теоремы.
Египетский треугольник является простейшим (и первым известным) из Героновых треугольников — треугольников с целочисленными сторонами и площадями.
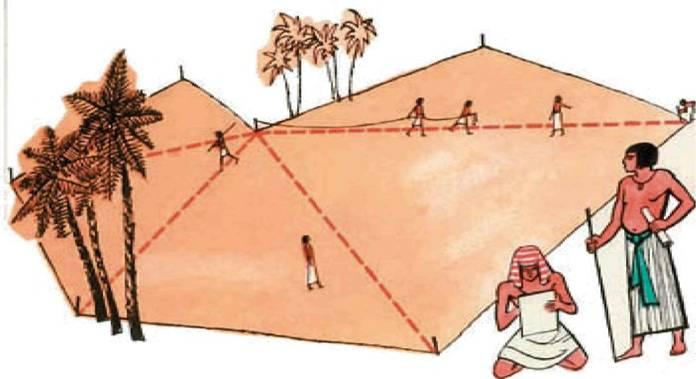
Египетский треугольник с соотношением сторон 3:4:5 активно применялся для построения прямых углов землемерами и архитекторами.
Для построения прямого угла использовался шнур или верёвка, разделённая отметками (узлами) на 12 (3+4+5) частей: треугольник, построенный натяжением такого шнура, с весьма высокой точностью оказывался прямоугольным и сами шнуры-катеты являлись направляющими для кладки прямого угла сооружения.. Применялся египетский треугольник в архитектуре средних веков для построения схем пропорциональности и для построения прямых углов землемерами и архитекторами.
Треуго́льник Рёло́ представляет собой область пересечения трёх равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне. Негладкая замкнутая кривая, ограничивающая эту фигуру, также называется треугольником Рёло.
Треугольник Рёло является простейшей после круга фигурой постоянной ширины. То есть если к треугольнику Рёло провести пару параллельных опорных прямых, то независимо от выбранного направления расстояние между ними будет постоянным. Это расстояние называется шириной треугольника Рёло.
Среди прочих фигур постоянной ширины треугольник Рёло выделяется рядом экстремальных свойств: наименьшей площадью, наименьшим возможным углом при вершине, наименьшей симметричностью относительно центра.
Название фигуры происходит от фамилии немецкого механика Франца Рёло. Он, вероятно, был первым, кто исследовал свойства этого треугольника; также он использовал его в своих механизмах.
2.1.3. Основные свойства треугольника.
Свойства треугольника, изучающиеся в школе, за редким исключением, известны с античности.
Теорема Чевы была доказана в XI веке арабским учёным Юсуфом аль-Мутаманом ибн Худом, однако его доказательство было забыто. Она была доказана вновь итальянским математиком Джованни Чевой в 1678 году.
Дальнейшее изучение треугольника началось в XVII веке: была доказана теорема Дезарга (1636), открыты некоторые свойства точки Торричелли (1659). В XVIII веке была обнаружена прямая Эйлера и окружность шести точек (1765). В 1828 году была доказана теорема Фейербаха. В начале XIX века была открыта точка Жергонна.
Многие факты, связанные с треугольником, были открыты в конце XIX века. К этому времени относится творчество Эмиля Лемуана, Анри Брокара, Жозефа Нейберга, Пьера Сонда́.
Во всяком треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы.
Каждый внешний угол треугольника равен разности между 180° и соответствующим внутренним углом. Для внешнего угла также имеет место теорема о внешнем угле треугольника: внешний угол равен сумме двух других внутренних углов, с ним не смежных .
В треугольнике сумма длин двух его сторон больше длины третьей стороны.
Дополнительное свойство: каждая сторона треугольника больше разности двух других сторон.
Теорема о сумме углов треугольник
Сумма внутренних углов треугольника всегда равна 180°:
В геометрии Лобачевского сумма углов треугольника всегда меньше 180°, а на сфере — всегда больше.
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов.
где R — радиус окружности, описанной вокруг треугольника.
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними Является обобщением теоремы Пифагора.
Теорема о проекциях
Из теоремы о проекциях следует то, что высота, опущенная, например, из вершины С, делит противоположную ей сторону АВ на две части и , считая от вершины А к В.
Свойство «жесткости треугольника».
Треугольник — жёсткая фигура. Представим себе две рейки, у которых два конца скреплены гвоздем. Такая конструкция не является жёсткой: сдвигая или раздвигая свободные концы реек, мы можем менять угол между ними. Теперь возьмем ещё одну рейку и скрепим её концы со свободными концами первых двух реек. Полученная конструкция — треугольник — будет уже жёсткой. В ней нельзя сдвинуть или раздвинуть никакие две стороны, т. е. нельзя изменить ни один угол. Действительно, если бы это удалось, то мы получили бы новый треугольник, не равный исходному. Но это невозможно, так как новый треугольник должен быть равен исходному по третьему признаку равенства треугольников.
Рассмотрим модели двух фигур — треугольника и четырёхугольника и выясним, можно ли, не меняя длины сторон, изменить форму фигуры? Под действием небольшой силы четырёхугольник изменил свою форму, а треугольник нет.
Вывод: можно сказать, что треугольник – не изменяющаяся фигура. В нем нельзя сдвинуть или раздвинуть никакие две стороны, в отличие от любого другого многоугольника. В треугольнике нельзя изменить ни один из углов. Таким образом, треугольник – жесткая фигура. Если заданы три его стороны, то форму треугольника уже изменить нельзя, не разрушив его. Это свойство широко используется на практике.
2.1.4. Замечательные точки треугольника
Замечательные точки треугольника — точки, местоположение которых однозначно определяется треугольником и не зависит от того, в каком порядке берутся стороны и вершины треугольника.
Обычно они расположены внутри треугольника, но и это не обязательно. В частности, точка пересечения высот может находиться вне треугольника.
Замечательными точками треугольника являются точки пересечения:
Факт того, что три медианы пересекаются в одной точке, был доказан ещё Архимедом.
- Центроид делит каждую медиану в отношении 2:1, считая от вершины.
- Если в вершины треугольника поместить равные массы, то центр масс полученной системы будет совпадать с центроидом. Более того, центр масс треугольника с равномерно распределённой массой также находится в центроиде.
- Если М — центроид треугольника , то для любой точки О верно равенство
- Центроид является точкой, для которой сумма квадратов расстояний до вершин треугольника принимает наименьшее значение (теорема Лейбница).
- Три отрезка прямых, соединяющих вершины треугольника с центроидом, разбивают данный треугольник на три равновеликих треугольника (равной площади).
- Три отрезка прямых, соединяющих середины сторон треугольника с центроидом, разбивают данный треугольник на три равновеликих четырёхугольника (равной площади).
- Сумма квадратов сторон треугольника равна утроенной сумме квадратов расстояний от центроида до вершин: треугольника.
- Центр вписанной окружности треугольника находится на одинаковом расстоянии от всех сторон треугольника.
В зависимости от вида треугольника ортоцентр может находиться внутри треугольника (в остроугольном), вне его (в тупоугольном) или совпадать с вершиной (в прямоугольном — совпадает с вершиной при прямом угле).
- Если в четвёрке точек А, В, С, D точка D является точкой пересечения высот треугольника ABC, то и любая из четырёх точек является ортоцентром треугольника, образованного тремя остальными точками. Такую четвёрку иногда называют ортоцентрической системой точек .
- Радиусы окружностей, проходящих через любые три точки ортоцентрической системы , равны (следствие теоремы Гамильтона для окружности Эйлера). Их часто называют окружностями Джонсона.
- Последнее утверждение можно сформулировать так: Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих равные радиусы описанных окружностей (следствие теоремы Гамильтона для окружности Эйлера). При этом одинаковый радиус этих трех окружностей равен радиусу окружности, описанной около исходного остроугольного треугольника.
- Ортоцентр лежит на одной прямой с центроидом , центром описанной окружности
- Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник .
- Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника. .
- Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности .
- Точки, симметричные ортоцентру треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
- Расстояние от центра описанной окружности до стороны равно . расстояние от ортоцентра до вершины равно .
Раздел III . Треугольники вокруг нас.
Изображения треугольников и задачи на треугольники встречаются во многих папирусах Древней Греции и Древнего Египта. Еще в древности стали вводить некоторые знаки обозначения для геометрических фигур.
Древнегреческий ученый Герон (I век) впервые применил знак вместо слова треугольник.
Треугольник является одной из первых геометрических фигур, которая стала использоваться в орнаментах древних народов.
Различные жилища людей: вигвам, юрта, палатка. Все они имеют конусообразную форму, в сечении получается треугольник. Такие сооружения легко обдуваются ветрами, с них быстро стекает вода. Крыши старых деревянных домов и современных многоэтажек имеют форму треугольника. Это связано с тем, что на таких крышах не задерживается талый снег и легко стекает дождевая вода.
Предметы одежды человека. Различные головные уборы: треуголки, пилотки, колпаки, косынки – имеют треугольную форму. Женские платки, прежде чем накинуть на голову, складывают пополам. При шитье юбки часто втачивают клинья, которые тоже имеют форму треугольника, что придает юбке пышность. Чтобы одежда не помялась, ее хранят на плечиках, имеющих треугольную форму.
Солдатский треугольник – письмо без марки и конверта, отправленное солдатом с фронта или солдату на фронт.
Пирами́да Хео́пса — крупнейшая из египетских пирамид , единственное из «Семи чудес света» , сохранившееся до наших дней. Строительство, продолжавшееся двадцать лет, началось около 2560 года до н. э.
На парусных судах используются паруса треугольной формы.
При создании букета или композиции нужно соблюдать гармонию цвета. При этом используется метод равностороннего треугольника .
Треугольник широко используется в предупреждающих знаках дорожного движения.
Широкое применение в жизни человека нашло свойство жесткости треугольника.
Символ Франции знаменитая Эйфелева башня — самая узнаваемая архитектурная достопримечательность Парижа. Колебания башни во время бурь не превышают 15 см. Это объясняется тем, что вся конструкция башни сплетена из треугольников, обладающих жёсткостью.
Во время Великой Отечественной войны для сохранения стекол во время бомбежки их заклеивали бумажными полосками, чтобы получился треугольник.
В основе геодезического купола лежит каркас, представляющий собой пространственную ферму в виде полусферы. Именно из треугольников и состоит основной каркас геокупола. Благодаря своей конструкции геодезические купола выдерживают нагрузки, в несколько раз превышающие допустимые нагрузки для обычных прямоугольных сооружений.
Так, чтобы закрепить столб в вертикальном положении, к нему ставят подпорку. Телеграфные столбы с подпоркой называют анкерными.
Стропила зданий имеют вид треугольников. Это придаёт им крепость и устойчивость.
При строительстве любых мостов в их конструкциях также присутствуют треугольники. Треугольники делают надежными конструкции высоковольтных линий электропередач.
Свойство жесткости треугольника широко используют в практике при строительстве железных конструкций.
п.3.1. Треугольник в математике.
Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля. Числа, составляющие треугольник Паскаля, возникают естественным образом в алгебре, комбинаторике, теории вероятностей, математическом анализе, теории чисел.
Треугольник Серпинского — фрактал, один из двумерных аналогов множества Кантора, предложенный польским математиком Вацлавом Серпинским в 1915 году. Также известен как «салфетка» Серпинского.
Середины сторон равностороннего треугольника соединяются отрезками. Получаются 4 новых треугольника. Из исходного треугольника удаляется внутренность срединного треугольника. Получается множество Т 1 , состоящее из 3 оставшихся треугольников «первого ранга». Поступая точно так же с каждым из треугольников первого ранга, получим множество Т 2 , состоящее из 9 равносторонних треугольников второго ранга. Продолжая этот процесс бесконечно, получим бесконечную последовательность Т n , пересечение членов которой есть треугольник Серпинского.
Важным свойством треугольника Серпинского является его самоподобие — ведь он состоит из трёх своих копий, уменьшенных в два раза (это части треугольника Серпинского, содержащиеся в маленьких треугольниках, примыкающих к углам).
Если в треугольнике Паскаля все нечётные числа окрасить в чёрный цвет, а чётные — в белый, то образуется треугольник Серпинского.
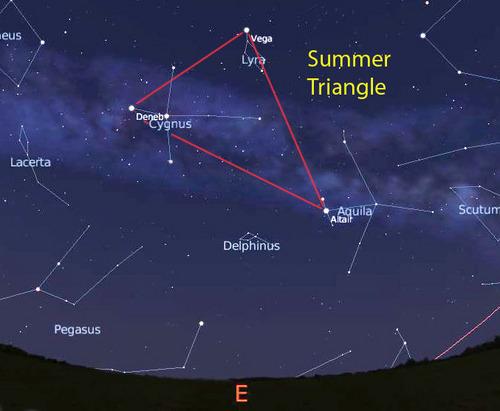
п.3.2. Треугольник в астрономии.
Треуго́льник (лат. Triangulum, Tri) — созвездие северного полушария неба. Занимает на небе площадь 131,8 квадратных градуса, содержит 25 звёзд, видимых невооружённым глазом.
В Треугольнике находится спиральная галактика M33 (галактика Треугольника), третья по величине в Местной группе.
Звезды Треугольника не ярки: α всего лишь третьей звёздной величины. Всего в созвездии можно насчитать 15 звёзд. В телескоп можно увидеть и двойную звезду ι, компоненты которой окрашены в золотисто-жёлтый и зелёно-голубой цвета.
Треугольник Кеплера.
В начале XVII в. знаменитый астроном Кеплер составил диаграмму соединения планет Сатурна и Юпитера. Так в астрономии называют расположение планет, при котором для земного наблюдателя эклиптические долготы равны нулю, а сами небесные тела находятся близко друг к другу или даже перекрываются. Кеплер представил это явление в виде треугольника , который вращается по зодиакальному кругу, совершая полный оборот за 2400 лет.
п.3.3. Треугольник в музыке.
Треуго́льник (итал. triangolo, англ. и фр. triangle, нем. Triangel) — ударный музыкальный инструмент в виде металлического прута (обычно из стали или алюминия), изогнутого в форме треугольника. Один из углов оставлен открытым (концы прута почти касаются).
Треугольник принадлежит к инструментам с неопределённой высотой звука, имеет блестящий и яркий тембр, способный украсить даже мощное оркестровое tutti. Как правило, ему поручаются несложные ритмические фигуры и тремоло. Треугольник подвешивается за один из углов на тонкой проволоке или тесьме, которую держат в руке или прикрепляют к пюпитру. По треугольнику ударяют металлической (реже деревянной) палочкой (на жаргоне музыкантов эта палочка называется «гвоздь»).
Треугольную форму имеют музыкальные инструменты : балалайка, арфа, треугольник.
Треугольники окружают нас повсюду: детские пирамидки, архитектурные сооружения, дорожные знаки, музыкальные инструменты. В повседневной жизни мы почти перестали их замечать, а ведь это очень интересно, знать историю привычных для всех предметов, тем более, если она так увлекательна.
С одной стороны, треугольники имеют тысячелетнюю историю, с другой — это современный раздел математики. Теория треугольников имеет большое значение не только для теоретических исследований по геометрии, но и для других наук.
«Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Всё вокруг – геометрия». Эти слова, сказанные великим французским архитектором Ле Корбюзье, в начале ХХ века, очень точно характеризуют и наше время.
Список использованной литературы
- Атанасян Л. С. Геометрия: Учеб. для общеобразоват. учреждений. – М.: Просвещение, 2002.
- За страницами учебника алгебры: Кн. для учащихся 7 – 9 кл. сред. Шк. — М.: Просвещение, 1990. – 224 с.: ил.
- Мякишев А. Г., Элементы геометрии треугольника., Москва, МЦНМО, 2002.
- Абачиев С. К. О треугольнике Паскаля, простых делителях и фрактальных структурах // В мире науки, 1989, № 9.
Видео:Треугольники. 7 класс.Скачать

Проект «Треугольники. они повсюду» , 7 класс
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Треугольники… они повсюду.
Авторы проекта Сапожникова Елена и Червенко Анисия
Руководитель: учитель математики Сидорова О.С.
2. Последовательность работы над проектом……………….………….….4
Список литературы и ресурсов…………………………………
Начиная с начальных классов на уроках математики мы познакомились с
геометрическими фигурами (луч, отрезок, прямая, угол, треугольник,
многоугольник, окружность, круг). Поэтому в 7 классе новый
учебный предмет — геометрия, не стал для нас абсолютной новостью. а именно решение задач по разным темам убедило нас в том, что
«Треугольник» — фигура, необходимая для решения большинства задач, поэтому мы решили исследовать важность этой фигуры не только в геометрии, но и в жизни человека.
Всѐ то, что мы видим вокруг (прямоугольник окна
или двери, загадочный узор снежинки, здания, капля воды, узел на верѐвке, орнаменты и многое другое, так или иначе относится к треугольникам, ничего не ускользает от его внимательного взгляда. В исследовательском проекте по теме «Треугольники… они повсюду» мы изучили историческую часть, провели исследовательскую и творческую работу. Мы изучили историю развития термина треугольник, рассмотрела геометрические сведения о треугольнике, а так же треугольник в окружающем нас мире. Продуктом нашей работы стал реферат и электронная презентация.
Актуальность данного исследовательского проекта определяется
важностью умения видеть математику в мире, в котором мы живѐм,
внимательно смотреть вокруг и видеть красоту обычных вещей.
Предметом исследования является рассмотрение истории развития
термина треугольник, геометрические сведения о треугольнике и
треугольник в окружающем нас мире.
Проблема: недостаточность сведений о роли треугольника в жизни людей.
Гипотеза : Треугольники окружают на повсюду.
1. Цели и задачи проекта
сформировать представление о понятии треугольник;
сформировать навыки и умения обобщения нового материала;
сформировать математическую грамотность.
Изучение исторических сведений о треугольниках
Исследование геометрических свойств: треугольника
Поиск информации о том, где встречаются треугольники в
окружающем нас мире;
2. Последовательность работы над проектом
Проблема и вытекающие из неѐ задачи исследования.
Сбор и систематизация информации темы.
Обработка полученных результатов.
Заключительная часть проекта.
Представление исследовательского проекта.
Из истории геометрии
Геометрия возникла очень давно, это одна из самых древних наук. Геометрия
(греческое, от ge — земля и metrein — измерять)— наука о пространстве,
точнее — наука о формах, размерах и границах тех частей пространства,
которые в нем занимают вещественные тела. Важную роль играли и
эстетические потребности людей: желание украсить свои жилища и одежду,
рисовать картины окружающей жизни. Все это способствовало
формированию и накоплению геометрических сведений. За несколько
столетий до нашей эры в Вавилоне, Китае, Египте и Греции уже
существовали начальные геометрические знания, которые добывались в
основном опытным путем, но они не были еще систематизированы и
передавались от поколения к поколению в виде правил и рецептов. Не было еще доказательств этих правил, и их изложение не представляло собой научной теории.
Первые шаги культуры всюду, где она возникала, в Китае, в Индии, в Ассирии, в Египте, были связаны с необходимостью измерять расстояния и участки на земле, объемы и веса материалов, продуктов, товаров. Традиционно считается, что родоначальниками геометрии являются древние греки, перенявшие у египтян ремесло землемерия и измерения объѐмов тел и превратившие его в науку.
Превращение это произошло путѐм абстрагирования от всяких свойств тел,
кроме взаимного положения и величины. Наукой геометрия стала, когда от
набора рецептов перешли к установлению общих закономерностей.
Центральное место среди древних трудов по геометрии занимают составленные около 300 до н. э. «Начала» Евклида. Этот труд и поныне остаѐтся образцовым изложением в духе аксиоматического метода: все положения выводятся логическим путѐм из небольшого числа явно указанных и не доказываемых предположений —
аксиом. Геометрия греков, называемая сегодня евклидовой, или
элементарной, занималась изучением простейших форм: прямых,
плоскостей, отрезков, правильных многоугольников и многогранников,
конических сечений, а также шаров, цилиндров, призм, пирамид и конусов.
Треугольник – самая простая замкнутая прямолинейная фигура, одна из
первых, свойства которых человек узнал еще в глубокой древности, т. к. эта
фигура всегда имела широкое применение в практической жизни.
Изображения треугольников и задачи на треугольники встречаются во
многих папирусах Древней Греции и Древнего Египта. Еще в древности
стали вводить некоторые знаки обозначения для геометрических фигур.
Древнегреческий ученый Герон (I век) впервые применил знак ∆ вместо
слова треугольник. Прямоугольный треугольник занимал почетное место в
Вавилонской геометрии. Стороны прямоугольного треугольника: гипотенуза
и катеты. Термин «гипотенуза» происходит от греческого слова
«ипонейноуза», обозначающее «тянущаяся над чем-либо», «стягивающая».
Слово берет начало от образа древнегреческих арф, на которых струны
натягиваются на концах двух взаимно-перпендикулярных подставок. Термин
«катет» происходит от греческого слова «катетос», которое означает начало
«отвес», «перпендикуляр». Евклид говорил: «Катеты – это стороны,
заключающие прямой угол». В Древней Греции уже был известен способ
построения прямоугольного треугольника на местности. Для этого
использовали веревку, на которой были завязаны 12 узелков, на одинаковом
расстоянии друг от друга. При строительстве пирамид в Египте именно так
изготавливали прямоугольные треугольники. Наверно поэтому
прямоугольный треугольник со сторонами 3,4,5 и назвали египетским
Пирамида Хеопса – крупнейшая и Египетских пирамид.
Предполагается, что строительство, продолжавшееся 20 лет закончилось
около 2560 года до нашей эры.
При
Определение: Треугольником называется фигура, которая состоит из
трѐх точек, не лежащих на одной прямой, и трѐх отрезков, попарно
соединяющие эти точки.
На рисунке изображѐн треугольник АВС и указаны основные его
Треугольник с вершинами A , B и C обозначается как Δ ABC . Треугольник
Δ ABC имеет три стороны:
Треугольник Δ ABC имеет следующие углы:
угол — угол ∠ ВАС, образованный сторонами AB и AC и
противолежащий стороне BC ;
угол — угол ∠ АВС, образованный сторонами AB и BC и
противолежащий стороне AC ;
угол — угол ∠ АСВ, образованный сторонами BC и AC и
противолежащий стороне AB .
Величины углов при соответствующих вершинах традиционно
обозначаются греческими буквами (α, β, γ). Всѐ большое семейство
треугольников можно разделить на группы.
По величине углов. Поскольку в евклидовой геометрии сумма углов
треугольника равна 180°, то не менее двух углов в треугольнике должны
быть острыми (меньшими 90°). Выделяют следующие виды треугольников:
Если все углы треугольника острые, то треугольник называется
Если один из углов треугольника тупой (больше 90°), то треугольник
Если один из углов треугольника прямой (равен 90°), то треугольник
называется прямоугольным. Две стороны, образующие прямой угол,
называются катетами, а сторона, противолежащая прямому углу, называется
По числу равных сторон :
Равнобедренным называется треугольник, у которого две стороны
равны. Эти стороны называются боковыми, третья сторона называется
основанием. В равнобедренном треугольнике углы при основании равны.
Равносторонним называется треугольник, у которого все три стороны
равны. В равностороннем треугольнике все углы равны 60°.
Важную роль в треугольнике играют такие отрезки как медианы, высоты и биссектрисы.
Медианой треугольника, проведѐнной из данной вершины, называется
отрезок, соединяющий эту вершину с серединой противолежащей стороны.
Высотой треугольника называется перпендикуляр, опущенный из
вершины на противоположную сторону или еѐ продолжение.
Биссектрисой треугольника называется отрезок биссектрисы угла треугольники, соединяющий его вершину с точкой противоположной стороны.
Мы изучили Признаки равенства треугольников
Треугольник на евклидовой плоскости однозначно можно определить по
следующим тройкам основных элементов:
1. a, b, γ (равенство по двум сторонам и углу лежащему между ними);
a, β, γ (равенство по стороне и двум прилежащим углам);
3.a, b, c (равенство по трѐм сторонам).
Мир, в котором мы живѐм, наполнен геометрией домов и улиц, гор и
полей, творениями природы и человека. Ведь во время работы мы были
архитекторами, кинематографами, фотографами. Наша задача состояла в том,чтобы показать встречаются ли в повседневной жизни треугольники и
В Древнем Египте он был прямоугольным и являлся воплощением триады духовной воли, любви и высшего разума человека.
На Древнем Востоке почитали треугольник как символ природы всего
сущего. Треугольник с вершиной, соединенной с такой же геометрической
фигурой, ацтеки использовали в качестве эмблемы временного цикла
Для средневековых алхимиков треугольник с вершиной, устремленной
вверх, являлся знаком пламени, «мужского огня», а при его наложении на
описанный выше знак женского начала мы получим индуистскую эмблему
объединения созидающего и порождающего начал —гексаграмму. В
буддийской традиции два смыкающихся треугольника олицетворяют чистое
пламя и Три Драгоценности Будды. Китайский символ восстановления
изображается в виде треугольника с подвешенными к нему мечами, а у
христиан —треугольника, образованного посредством трех пересекающихся
окружностей. Это олицетворяет Троицу в единении и равенстве трех ее
составляющих. Два соединенных вершинами вертикальных треугольника
разделяют символизм песочных часов, олицетворяя неумолимо идущее время
и смертность. Также песочные часы часто используются для обозначения
благочестивого, тихого образа жизни, краткости человеческой жизни, а также
применяются как атрибут отца-времени и порой даже смерти.
Троица и треугольник
Начиная с ранних христиан треугольник был символом Святой Троицы.
Равносторонний треугольник толковался как равенство и единая
божественная сущность Бога Отца, Бога Сына и Духа Святого. Иногда этот
символ составляли из трех переплетенных между собой рыб. Символ Троицы
по католической традиции составлялся из трех малых треугольников,
вписанных в один большой с кругами на вершинах. Три этих круга означают
триединство, но каждый круг независим и совершенен сам по себе. Эта схема
иллюстрировала принцип триединства и вместе с тем индивидуальности
каждого составляющего Святой Троицы.
Печать Соломона — другое название звезды Давида, образованной
наложением друг на друга двух треугольников, т.е. гексаграммы. По
преданию, царь Соломон с помощью этого знака управлял духами,
заключенными в медный сосуд. Считается, что печать Соломона является
мощным амулетом, способным защитить своего обладателя от влияния злых
Вначале XVII в. знаменитый астроном Кеплер составил диаграмму
соединения планет Сатурна и Юпитера. Так в астрономии называют
расположение планет, при котором для земного наблюдателя эклиптические
долготы равны нулю, а сами небесные тела находятся близко друг к другу
или даже перекрываются. Кеплер представил это явление в виде
треугольника, который вращается по зодиакальному кругу, совершая полный
оборот за 2400 лет
Треугольник в античной архитектуре
В античной традиции треугольник, обращенный вершиной вверх,
символизировал стремление материи к духу. Поэтому фронтоны
древнегреческих храмов в самой глубокой древности делали треугольными и
всячески украшали. В отличие от поздних, более северных европейских
построек наличие двускатной крыши не было вызвано климатическими
условиями. В Древней Греции был теплыйклимат и снега зимой не было
Треугольники на сосудах
В эпоху неолита у ранних земледельческих народов треугольники в
орнаментах символизировали воздух, землю и огонь. Они — одни из самых
древних символов, связанных с сельскохозяйственными работами, природой
и ее календарными циклами.
Точное происхождение названия этого созвездия неизвестно. Свое
название оно получило на Древнем Востоке, его знали и использовали в
навигации финикийские мореходы. Для них оно символизировало
священный камень пирамидальной формы. Треугольник входил в число 48
классических созвездий античности. Древние греки считали, что это —
перенесенная на небо дельта Нила, что указывает на египетские корни
названия созвездия. Уже в Новое время на звездном небе были выделены
созвездия Южного Треугольника и Наугольника.
Бермудский треугольник — район в Атлантическом океане, в котором
якобы происходят таинственные исчезновения морских и воздушных судов.
Бермудский треугольник – одна из наиболее известных и освещенных
аномальных зон планеты. Расположенный между Пуэрто-Рико, американской
Флоридой и южными Бермудскими островами, в восточной части Саргассова
моря, он получил известность начиная с 1492 года. Еще тогда в вахтенном
журнале «Санта Марии», флагманского корабля Колумбовой экспедиции
были оставлены записи о странных событиях, сопровождавших плавание по
водам Бермудского треугольника – воды, полностью заросшие водорослями,
странное поведение стрелки компаса вблизи границ Саргассова моря,
необъяснимое свечение неба и моря, огромный, возникший внезапно и
внезапно пропавший язык пламени.
Тайны бермудского треугольника
Официально считается что в 1840 году Бермудский треугольник
получил свое название и известность. Именно в этом году недалеко от
Багамских островов (район порта Нассау) в море было обнаружено
дрейфующее судно «Розалия» (Франция), все парусное оснащение и груз
которого были в порядке, а на борту отсутствовала команда. На настоящее
время в районе Бермудского треугольника без следа исчезли более тысячи
человек, и официально зарегистрировано больше полутора сотен случаев
таинственного исчезновения самолетов и кораблей. При этом не удается
найти никаких следов крушения – ни обломков, ни масляных пятен. Самым
известным и необъяснимым исчезновением летательных аппаратов в районе
Бермудского треугольника из задокументированных остается исчезновение
пяти бомбардировщиков ВМФ США 5 декабря 1945 года, причем во время
проведения поисков вслед за ними исчез и самолет спасателей. Но
Бермудский треугольник далеко не всегда и совсем не для всех представляет
опасность. Огромное количество самолетов и кораблей совершенно без
всякой опасности проходили через эту зону, не наблюдая и следа
паранормальных явлений. Нет никакой информации о том, что может
провоцировать аномальную активность Бермудского треугольника. Для
ученых Бермудский треугольник представляет интерес по многим причинам.
«Море Вуду» исследовали на рельеф морского дна, на наличие минералов и
нефти, исследовали геологическое строение океанического дна в этом
районе. Хотя некоторые энтузиасты и спекулируют этими исследованиями,
надо помнить, что ученые исследовали этот регион не в поисках объяснения
загадочных событий. Тайны Бермудского треугольника и в настоящее время
не имеют никаких внятных объяснений, несмотря на большое количество
документальных фото бермудского треугольника, видео, и материалов
Герб и треугольник
На гербах различных стран мы часто можем видеть треугольник,
вписанный в окружность. Это изображение олицетворяет собой мир форм,
заключенный в круге вечности. Изображенный на гербе треугольник так
же означает равенство, демократию.
Герб и флаг Сальвадора. Герб г.Неман Калининградская обл.
В мире можно найти много различных предметов треугольной формы или очень похожей на нее. Так как это одна из простейших фигур, то и употребляется она часто в разных ситуациях:
1. Корона. Состоит из маленьких треугольников, является символом
2.Стрелка. А вернее, ее наконечник.
3. Нос корабля в виде треугольника
4. Журавли прилетают стаями. Перелеты в форме треугольника.
5. На гербах городов и некоторых стран.
6. Железная руда (условные обозначения).
7. Условные обозначения на картах в принципе часто используют
Железная руда (условные обозначения).
Природный газ. (условные обозначения)
Деревья на картах
8.Детские рисунки «ѐлочки» и «человечков»
10. Клубника, кусочек арбуза
14. Чай в пакетиках-пирамидках
15. Некоторые дорожные знаки
16. Кусок сыра (пирога, пиццы и т.д.)
17. Зубчик чеснока (зависит, собственно, от чеснока)
19. Развилка дорог
20. Некоторые виды столов
22. Треугольник в бильярде (для сбора всех шариков)
23. Пионерский галстук
24. Кошачьи или собачьи уши
25. Название фильмов:
«Треугольник» — армянский художественный фильм 1967 года.
Треугольник- спальный район расположенный на окраине города.
«Треугольник» — англо-австралийский мистический триллер 2009
«Чѐрный треугольник» — советский телевизионный художественный
фильм 1981 года.
«Русский треугольник» — художественный фильм 2007 года.
27. Утюг (подошва)
29. Различные значения:
Треугольник — удушающий приѐм.
Треугольник — способ передачи очереди хода сопернику в шахматах.
Треугольник — знак различия на петлицах сержантов и старшин
в Красной Армии.
Треугольник — вид соединения электрических цепей. (физика)
Треугольник – ударный музыкальный инструмент в виде
металлического прута, изогнутого в форме треугольника. Один из углов
Около 30 наименований и можно продолжать и продолжать.
При разложении товаров на прилавках супермаркетов, обязательно учитывают правило «золотого треугольника», основанное на психологии покупателя.
В строительстве и архитектуре большое значение имеет такое свойство фигуры треугольник как его жесткость.
Что такое жесткая фигура? Почему треугольник — жесткая фигура?
Жесткая фигура — это фигура, не подверженная деформации.

С треугольником так поступить не удастся. Стороны треугольника определяют его углы однозначно. Поэтому треугольник — жесткая фигура.
Из всех многоугольников только треугольник является жесткой фигурой.
Это свойство треугольника используется, в частности, при создании железных ажурных конструкций.
Рассматривая термин, треугольник в окружающем нас мире мы увидели, что
математика часть общечеловеческой культуры и мир геометрии –
увлекателен и интересен.
При работе с этим проектом мы убедились, что, треугольники связанны с
другими учебными дисциплинами, такими как история, мифология,
литература, география, астрономия, физика, химия, религиоведение. Работая
над проектом, мы увидели красоту обычных вещей и внимательно смотрели
вокруг, находили, систематизировали информацию и выделяли значимое.
Результат работы — электронное приложение реферат, которые мы
представим на уроках математики 6-7 классах.
Мы надеемся, что наша работа заинтересует вас. Мы считаем, что этот проектпоможет учащимся лучше ориентироваться в математике, открывать новое,понимать красоту, мудрость окружающего мира и учащиеся лучше смогут увидеть, что понятия не изолированы друг от друга, а представляют
определѐнную систему знаний, все звенья которой находятся во взаимной
«Я думаю, что никогда до настоящего времени мы не жили в такой
геометрический период. Всѐ вокруг – геометрия». Эти слова, сказанные
великим французским архитектором Ле Корбюзье, в начале ХХ века, очень
точно характеризуют и наше время.
Список литературы и ресурсов
Демпан И.Я. Мир чисел: «Рассказы о математике»- Издание 4-е 1982г
Нагибин Ф.Ф.,Канин Е. С.Математическая шкатулка. Москва «Просвещение» 1984 г.
Е . Е. Семёнов. Изучаем геометрию. Москва « Просвещение »1987г.
Л.А.Бахтина. Час занимательной математики. Москва «Народное образование» 2003г.
Ю.В.Прохоров , С.А .Теляковский. «Научное издательство –Большая Российская Энциклопедия». Москва 1996 г.
Видео:Вся геометрия треугольника в одной задаче. Планиметрия. ЕГЭ 2023 математика задача 16Скачать

Проект по теме «Треугольники»
Проект по теме «Треугольники». Работа содержит материал о треугольниках.
Просмотр содержимого документа
«Проект по теме «Треугольники»»
Название проекта: Что вы знаете о треугольнике?
Учебный предмет, в рамках которого разрабатывается проект: математика.
По виду деятельности – информационный;
По организационной форме – групповой;
По содержанию – межпредметный;
По времени выполнения – долговременный (несколько недель).
Цель проекта: систематизировать и расширить знания о треугольнике.
Используя толковые словари русского языка, найти значение термина треугольник.
Рассмотреть основные виды треугольников и дать определение, каждого из этих треугольников.
Изучить историю возникновения треугольника.
Узнать о применении треугольников в практической жизни.
Руководитель проекта: М. С. Терехова, учитель математики МОУ «Стальновская школа»
Возраст участников проекта: 11-12 лет.
Аннотация проекта. Проект направлен на обобщение и систематизацию знаний по теме «Треугольник».Треугольник по праву считается простейшей из фигур: любая плоская, то есть простирающаяся в двух измерениях, фигура должна содержать хотя бы три точки, не лежащие на одной прямой. Треугольник всегда имел широкое применение в практической жизни.
Планируемый результат: презентация, выступление учащихся на уроке.
Этапы работы над проектом. Рекомендации для учащихся.
Используя толковые словари русского языка, дать определение термина треугольник.
История возникновения треугольника
Описание примеров практического применения треугольника.
Разделите работу на этапы
Подготовьте план работы над проектом.
Работайте по плану
Совместно решайте возникающие проблемы
При необходимости вносите изменения в план
При необходимости воспользуйтесь консультацией учителя или помощью родителей.
К намеченному времени объедините информацию в одну папку
Сгруппируйте слайды по каждому этапу проекта в итоговой презентации с одним заголовком.
Подготовьте выступление перед классом.
Выступите с проектом. Ответьте на вопросы слушателей.
Необходимое оборудование: компьютер, подключенный к сети Интернет, проекционная аппаратура для презентации; словари, литература по теме «Треугольник» и по истории возникновения треугольника; предметы треугольной формы.
«Когда острый угол треугольника касается круга, эффект не менее значителен, чем у Микеланджело, когда палец Бога касается пальца Адама». В.В.Кандинский.
ОПРЕДЕЛЕНИЕ ТЕРМИНА «ТРЕУГОЛЬНИК»
Определение слова «треугольник» в толковых словарях русского языка
Толковый словарь Ожегова С.И.
Геометрическая фигура — многоугольник с тремя углами, а также всякий предмет, устройство такой формы.
Прямоугольный треугольник, деревянный треугольник, солдатский треугольник.
Название сержантского и старшинского знака различия такой формы на петлицах в Красной Армии (с 1919 по 1943 г.)
В советском учреждении, на предприятии: совместно действующие три руководящих лица — администратор, секретарь партийной организации и председатель профсоюзного комитета
Толковый словарь Ушакова
Геометрическая фигура, ограниченная тремя взаимно пересекающимися прямыми, образующими три внутренних угла (мат.).
Всякий предмет, устройство, имеющие форму такой фигуры.
Ударный музыкальный инструмент из согнутого в форме такой фигуры стального прута, по которому ударяют металлической палочкой (муз)
В учреждении, предприятии или их отделах — общее название для трех руководящих лиц: руководителя по административной линии и руководителей по линии партийной и профсоюзной работы.
Словарь Ефремовой Т.Ф.
Геометрическая фигура на плоскости, ограниченная тремя пересекающимися прямыми, образующими три внутренних угла.
Три человека (двое мужчин и одна женщина или две женщины и один мужчина), связанные любовными отношениями
Какие виды треугольников существуют и каким образом их классифицируют?
В зависимости от величин углов различают следующие виды треугольников.
Треугольник, у которого все углы являются острыми.
Треугольник, у которого один из углов прямой.
Треугольник, у которого один из углов тупой.
В зависимости от соотношения длин сторон различают следующие виды треугольников.
Треугольник, у которого все стороны имеют различную длину.
Треугольник, у которого две его стороны равны между собой. Сторона, не равная двум другим, называется его основанием.
Треугольник, у которого все три его стороны равны между собой.
ИСТОРИЯ ПОЯВЛЕНИЯ ТРЕУГОЛЬНИКА
Крупнейший древнегреческий историк Геродот (V век до нашей эры) оставил описание того, как египтяне после каждого разлива Нила заново размечали плодородные участки его берегов, с которых ушла вода. C этого момента и началась геометрия – «землемерие» ( от греческого «гео» — «земля» и «метрео» — измеряю ).
Древнее землемеры выполняли геометрические построения, измеряли длины и площади; астрологии рассчитывали расположение небесных светил – всё это требовало весьма обширных познаний о свойствах плоских и пространственных фигур, и в первую очередь о треугольнике.
Изображение треугольников и задачи на треугольники встречаются в египетских папирусах, которым более 4000 лет, в старинных индийских книгах и других древних документах. Уже тогда была известна теорема, получившая впоследствии название теоремы Пифагора, которая применялась для построения прямых углов на местности с помощью веревочного треугольника со сторонами 3, 4, 5 (египетский треугольник).
Через 2000 лет в древней Греции учение о треугольнике достигает высокого уровня. Известны такие древнегреческие ученые, как Архимед, Пифагор, Фалес.
Учение о треугольнике развивалось в ионийской школе, основанной в VII веке до нашей эры Фалесом, затем в школе Пифагора. Древние греки решили упорядочить накопленные сведения о треугольнике и написали много трудов. Наиболее совершенной оказалась работа Евклида «Начала» (365-300 до н.э.).
Понятие о треугольнике исторически развивалось, по-видимому, так: сначала рассматривались лишь правильные, затем равнобедренные и, наконец, разносторонние треугольники.
Несколько тысячелетий геометры столь подробно изучили треугольник, что иногда говорят о «геометрии треугольника» как о самостоятельном разделе элементарной геометрии.
ТРЕУГОЛЬНИК В ЖИВОПИСИ
Творчество Василия Васильевича Кандинского – уникальное явление русского и европейского искусства. Именно этому художнику, наделённому могучим дарованием, блестящим интеллектом и тонкой духовной интуицией, суждено было совершить подлинный переворот в живописи и создать первые абстрактные композиции.
По Кандинскому, именно линия и цветовое пятно, а не сюжет являются носителями духовного начала, их сочетания рождают «внутренний звук», вызывающий отклик в душе зрителя. Наряду с треугольниками и квадратами композиции включали в себя круг как символ совершенства и полноты мироздания.
Чтобы зрители лучше понимали его картины, он написал книгу «Линия и точка на плоскости».
В «Вибрации» мы видим именно этот «контакт между острым треугольником и кругом», который художник называет «новым Адамом», тянущимся к Богу, как у Микеланджело.
В картинах «Точки на дуге» и «Три треугольника» можно увидеть, как треугольники применяются в живописи.
«Точки на дуге», 1927 г. «Три треугольника», 1938 г.
Портрет Моны Лизы привлекает тем, что композиция рисунка построена на»золотых треугольниках» (точнее на треугольниках, являющихся кусками правильного звездчатого пятиугольника).
Леонардо да Винчи — Мона Лиза
ТРЕУГОЛЬНИК В МУЗЫКЕ
Треугольник. Этим геометрическим термином называется музыкальный инструмент, который входит в группу ударных и довольно часто применяется в симфонической и оперной музыке. По форме инструмент представляет собой равносторонний треугольник. Сделан он из стального прута. Треугольник подвешивают к пульту и легонько ударяют металлической палочкой. Звук получается высокий (неопределенной высоты), звонкий и нежный, а при сильном ударе пронзительный, напоминающий колокольчики. В музыке Грига к драме Ибсена «Пер Гюнт» треугольник введен в танец Анитры. Его звенящая трель подчеркивает изящный, капризный характер танца. А в «Шехеразаде» и «Испанском каприччио» Римского-Корсакова ритмичное позвякивание треугольника придает музыке еще больший блеск, живость, задор.
ТРЕУГОЛЬНИК В ПРИРОДЕ
Бермудский Треугольник — широко известная аномальная зона. Расположен он в границах между Бермудскими островами, Майями во Флориде и Пуэрто-Рико. Площадь Бермудского треугольника составляет свыше одного миллиона квадратных километров. Рельеф дна в этой акватории хорошо изучен. На шельфе, который составляет значительную часть этого дна, было проведено множество бурений с целью отыскать нефть и другие полезные ископаемые. Течение, температура воды в разное время года, ее соленость и движение воздушных масс над океаном — все эти природные данные занесены во все специальные каталоги. Этот район не особенно сильно отличается от других похожих географических мест. И тем не менее именно в районе Бермудского треугольника загадочно исчезали суда, а затем и самолеты.
Обыкновенный богомол — насекомое, относящееся к семейству настоящих богомолов. Это самый распространенный представитель вида на территории Европы. Это довольно крупное насекомое. Голова у богомола треугольной формы, очень подвижная, соединенная с грудью. Она может вращаться на 180 градусов. У этого насекомого отлично развиты передние лапы, которые имеют мощные и острые шипы. С их помощью оно хватает свою жертву, а затем съедает ее.
ТРЕУГОЛЬНИК В АСТРОНОМИИ
Треугольник (лат. Triangulum, Tri) — созвездие северного полушария неба. Занимает на небе площадь 131,8 квадратных градуса, содержит 25 звёзд, видимых невооружённым глазом.
ТРЕУГОЛЬНИКЕ В АРХИТЕКТУРЕ
Египетские пирамиды тоже в форме треугольника. Пирамида имеет квадрат в плане и треугольник в вертикальном сечении, квадрат соответствует кресту, образованному четырьмя кардинальными точками.
Пирамида Лувра в Париже состоит из 603 ромбов и 70 треугольников из прозрачного стекла толщиной 21 миллиметр. Длина одной стороны основания – 35 метров, угол наклонна стороны 52 градуса. Общий вес пирамиды — 180 тонн.
Небоскреб Утюг является одним из самых известных исторических памятников Нью-Йорка. Знаковое строение высотой в двадцать один этаж известно своей треугольной формой, за что оно и получило название утюга. Этот дом был одной из первых впечатляющих высоток, выстроенных на Манхэттене.
Для проведения Универсиады 2011 в Шэньчжэне, Китай, был построен новый спортивный комплекс. Стадионы напоминают три многогранные светящиеся короны, изготовленные из стеклянных треугольников. Над созданием этой ювелирной работы крупного масштаба работала немецкая студия GMP Architekten.
Небоскрёб Мэри-Экс в Лондоне или Башня Сент-Мэри Экс, 30 (английское наименование 30 St Mary Axe) – это 40-этажное здание, расположенное в столице Великобритании, конструкция которого исполнена в виде сетчатой оболочки с центральным опорным основанием. В здании 5500 треугольных окон. С последних этажей небоскрёба открывается прекрасный панорамный вид на центральную часть Лондона.
Проект под названием NOAH (New Orleans Arcology Habitat) — смелый проект представляет собой треугольное здание высотой 365 метров, своеобразную городскую платформу, расположенную на воде. Необычная форма здания, в данном случае, несет функциональную нагрузку, ведь треугольник является одной из самых устойчивых фигур, а в Орлеане, подверженному ураганам, способность противостоять природной стихии является главенствующей. Треугольник также позволяет сделать здание сквозным, деля NOAH на три отдельных «башни», сходящиеся наверху. Назначение этой системы состоит в том, чтобы рассеивать сильные ветра, уменьшая нагрузку на здание. Для этой же цели внешние края здания изогнуты и наклонены.
Дизайн-студия Parsonson Architects представила проект Salamanca House в родном городе Веллингтон, Новая Зеландия. Жилой дом площадью 225 кв.м. расположен на крутом склоне и представлен двумя этажами. Учитывая малую площадь территории, отведенной под постройку, архитекторы максимально задействовали каждый метр. Спальня и гараж были спроектированы на нижнем уровне, что дало возможность расположить гостиную на втором этаже, объединив ее с кухней и столовой.
ТРЕУГОЛЬНИК И СИМВОЛЫ
Звезда Давида — шестиконечная звезда или гексаграмма, состоит из двух равносторонних треугольников, наложенных друг на друга: символ еврейского народа, знак, размещённый на флаге Государства Израиль. Шестиконечные звёзды также встречаются в символике других государств и населённых пунктов.
Оккультный знак «глаз в треугольнике» (или «Всевидящее око», или «сияющая дельта») считается символом Бога. Происхождение свое он ведет с глубокой древности. Возможно, традиция изображать подобным образом божество берет свое начало еще в Древнем Египте. В этом государстве часто использовался религиозный знак «соколиное око Гора». Треугольник также считается магическим знаком с давних времен.
ТРЕУГОЛЬНИК В ЖИЗНИ
Начиная игру в бильярд, необходимо расположить шары в виде треугольника. Для этого используют специальную треугольную рамку.
Головку сыра и торт часто разрезают на кусочки треугольной формы.
Знаки дорожного движения тоже состоят из треугольников.
В последнее время модными становятся дачи и дома в форме треугольника.
Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля. Числа, составляющие треугольник Паскаля, возникают естественным образом в алгебре, комбинаторике, теории вероятностей, математическом анализе, теории чисел
Треугольник — простейшая плоская фигура: три вершины и три стороны. Но с древнейших времен и до наших дней математики занимаются изучением треугольника. За это время было сделано много важных открытий и даже создана новая наука – тригонометрия.
Исходя из всего этого, можно сделать вывод, что треугольник является важнейшей и неисчерпаемой фигурой в геометрии.
📹 Видео
ВСЕ ВИДЫ ТРЕУГОЛЬНИКОВ😉 #егэ #огэ #математика #профильныйегэ #shorts #геометрия #образованиеСкачать

Средняя линия треугольника и трапеции. 8 класс.Скачать

90 задач по геометрии решается этим способом!Скачать
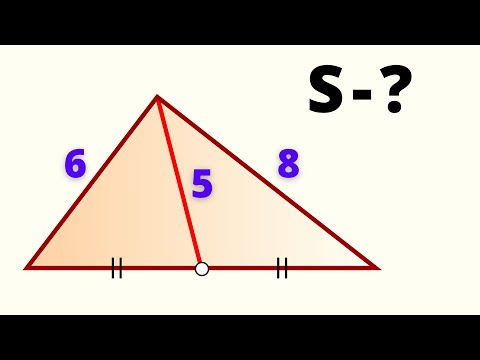
Неравенства треугольника. 7 класс.Скачать

Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Две задачи по геометрии за 7 класс на тему: "Треугольники"Скачать

Площадь Сечения: Разбираемся в Тайнах ГеометрииСкачать

Проверь свои знания по математике за 11 классСкачать

🔥 ФОКУС с треугольником #shortsСкачать

Лайфхак! Площади всех фигур #огэ #математика #shortsСкачать

Найдите угол: задача по геометрииСкачать

Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Свойства равнобедренного треугольника #огэ #математика #shortsСкачать

Реши задачу по геометрии #shortsСкачать

Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать