Треугольник является базовой фигурой геометрии, встречающейся повсеместно. Расчет всех геометрических фигур и тел основаны на наличии в них тех или иных треугольников, благодаря чему становится возможным применить множество теорем и формул, несвойственных конкретным фигурам по отдельности. Равносторонние треугольники, равнобедренные треугольники и прямоугольные треугольники составляют каркас решения геометрических задач, и обладая множеством дополнительных построений внутри треугольника, они предоставляют огромное количество значений тех или иных длин. Все биссектрисы, медианы, высоты, радиусы окружностей, вписанных или описанных около таких треугольников, можно рассчитать в этом разделе через геометрический калькулятор. Для этого необходимо ввести любые имеющиеся вводные данные, и калькулятор выдаст не только значения всех остальных параметров треугольника, но и объяснит преобразования формул, использованные для этих расчетов.
- Произвольный треугольник по заданным параметрам
- Синтаксис
- Примеры
- Параметры треугольника по заданным параметрам
- Сторона a = 8
- Сторона b = 2.1283555449519
- Сторона c = 7.5420719851515
- Полупериметр p = 8.8352137650517
- Угол А = 2.1882518638666 в градусах 125.37759631119
- Угол B = 2.873202966917 в градусах 164.62240368881
- Угол C = 1.221730476396 в градусах 70
- Площадь треугольника S = 8
- Высота ha на сторону a = 2
- Высота hb на сторону b = 7.5175409662872
- Высота hc на сторону c = 2.1214329472723
- Медиана ma на сторону a = 3.8348889915443
- Медиана mb на сторону b = 7.7012304590352
- Медиана mc на сторону c = 4.4770789813853
- Решение треугольников онлайн
- Решение треугольника по трем сторонам
- Решение треугольника по двум сторонам и углу между ними
- Решение треугольника по стороне и любым двум углам
- 🎦 Видео
Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Произвольный треугольник по заданным параметрам
| Введите известные даные треугольника | |
| Сторона а | |
| Сторона b | |
| Сторона c | |
| Угол А в градусах | |
| Угол B в градусах | |
| Угол C в градусах | |
| Медиана на сторону а | |
| Медиана на сторону b | |
| Медиана на сторону c | |
| Высота на сторону a | |
| Высота на сторону b | |
| Высота на сторону c | |
| Координаты вершины А | |
| X Y | |
| Координаты вершины B | |
| X Y | |
| Координаты вершины C | |
| X Y | |
| Площадь треугольника S | |
| Полупериметр сторон треугольника p | |
| Результат расчета параметров заданного треугольника | |||||||||||||||||||||||||||||||
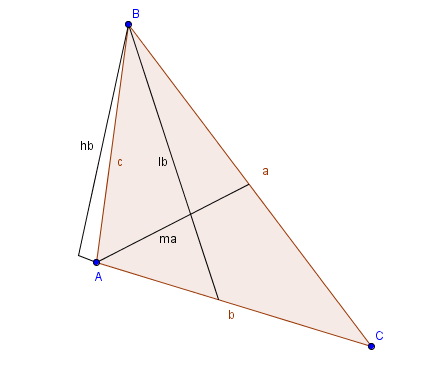
Представляем Вам калькулятор, который позволял рассчитывать все возможные параметры треугольника по заданным параметрам. Хотелось бы обратить Ваше внимание именно на то, что это универсальный бот. Он рассчитывает все параметры произвольного треугольника, при произвольно заданных параметрах. Такого бота вы не найдете нигде. Вам известна сторона и две высоты? или две стороны и медиана? Или биссектриса два угла и основание треугольника? По любым запросам, мы можем получить правильный расчет параметров треугольника. Вам нет необходимости искать формулы и делать расчет самостоятельно. За вас уже все сделано. Создайте запрос и получите точный ответ. Показан произвольный треугольник. Сразу оговоримся как и что обозначается, дабы в дальнейшем не было путаницы и ошибок в расчетах. Стороны противоположные любому углу называются так же только маленькой буквой. То есть напротив угла А лежит сторона треугольника а, стороне с противостоит угол С. ma — это медина, падающая на сторону а, соответственно есть еще медианы mb и mc падающие на соответствующие стороны. lb — это биссектриса , падающая на сторону b, соответственно есть еще биссектрисы la и lc падающие на соответствующие стороны. hb — это высота, падающая на сторону b, соответственно есть еще высоты ha и hc падающие на соответствующие стороны. Ну и второе, помните что треугольником является фигура в которой присутствует фундаментальное правило: Сумма любых(!) двух сторон должна быть больше третьей. Поэтому не удивляйтесь если получите ошибку При таких данных треугольника не существует при попытке рассчитатать параметры треугольника со сторонами 3, 3 и 7. Видео:Виды треугольниковСкачать  СинтаксисДля позволяателей XMPP клиентов запрос вот такой treug Для пользователй сайта, все сделано на этой странице. Список параметров — параметры которые известны, разделенные точкой с запятой параметр записываетя как параметр=значение Например если известна сторона а с значением 10, то так и записываем a=10 Более того, значения могут быть не только в виде вещественного числа, но и например как результат какого то выражения Например если нам нужно посчитать площадь треугольника с сторонами 1, 3, А вот и сам список парметров которые могут фигурировать в расчетах. Площадь треугольника S Высота ha на сторону a Высота hb на сторону b Высота hc на сторону c Медиана ma на сторону a Медиана mb на сторону b Медиана mc на сторону c Координаты вершин (xa,ya) (xb,yb) (xc,yc) Видео:Площади треугольников с равным углом.Скачать  ПримерыРассчитать параметры треугольника если известны сторона = 8, угол прилежащей к этой стороне =70 градусов и высота, падающая на эту сторону =2 пишем treug a=8;C=70;ha=2 Параметры треугольника по заданным параметрамСторона a = 8Сторона b = 2.1283555449519Сторона c = 7.5420719851515Полупериметр p = 8.8352137650517Угол А = 2.1882518638666 в градусах 125.37759631119Угол B = 2.873202966917 в градусах 164.62240368881Угол C = 1.221730476396 в градусах 70Площадь треугольника S = 8Высота ha на сторону a = 2Высота hb на сторону b = 7.5175409662872Высота hc на сторону c = 2.1214329472723Медиана ma на сторону a = 3.8348889915443Медиана mb на сторону b = 7.7012304590352Медиана mc на сторону c = 4.4770789813853Вот и все, все параметры треугольника. Вопрос, почему мы сторону назвали а, а не в или с? Это не влияет на решение. Главное выдержать условие о котором я уже сказал «Стороны противоположные любому углу называются так же, только маленькой буквой.» А далее нарисовать в уме треугольник, и применить к заданному вопросу. Можно было бы взять вместо а в, но тогда прилежащий угол будет не С а А ну и высота будет hb. Результат если вы проверите, будет один и тот же. Как рассчитать треугольник если известны координаты его вершин? Например вот такими (xa,ya) =3,4 (xb,yb) =-6,14 (xc,yc)=-6,-3 пишем запрос treug xa=3;ya=4;xb=-6;yb=14;xc=-6;yc=-3 Видео:Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать  Решение треугольников онлайнС помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже. Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°. Видео:Геометрия 7 класс (Урок№23 - Сумма углов треугольника.)Скачать  Решение треугольника по трем сторонамПусть известны три стороны треугольника a, b, c (Рис.1). Найдем
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения
Пример 1. Известны стороны треугольника ABC: Решение. Из формул (1) и (2) находим:
И, наконец, находим угол C:
Видео:Теперь ты будешь находить углы за секунды. Как найти внешний угол треугольника? #математика #углыСкачать  Решение треугольника по двум сторонам и углу между нимиПусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
Найдем сторону c используя теорему косинусов:
Далее, из формулы
Далее из (3) с помощью калькулятора находим угол A. Поскольку уже нам известны два угла то находим третий:
Пример 2. Известны две стороны треугольника ABC: Решение. Иcпользуя теорму косинусов найдем сторону c:
Из формулы (3) найдем cosA:
Поскольку уже нам известны два угла то находим третий:
Видео:Внешний угол треугольникаСкачать  Решение треугольника по стороне и любым двум угламПусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
Так как, уже известны два угла, то можно найти третий:
Далее, для находждения сторон b и c воспользуемся тероемой синусов:
Пример 3. Известна одна сторона треугольника ABC: Решение. Поскольку известны два угла, то легко можно найти третий угол С:
Найдем сторону b. Из теоремы синусов имеем:
Найдем сторону с. Из теоремы синусов имеем: 🎦 Видеовиды треугольников по угламСкачать  Углы треугольникаСкачать 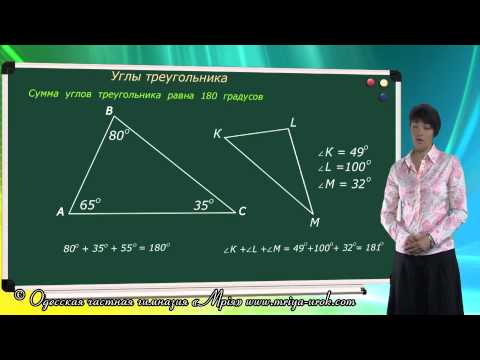 Геометрия 7 класс (Урок№9 - Треугольник.)Скачать  Классификация треугольников по сторонам и по угламСкачать  Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать  Отношение площадей треугольников с равным угломСкачать  Как найти величины углов всех треугольников. Сумма углов треугольника. Геометрия 7 класс.Скачать  #11 Генератор треугольников CSS Triangle GeneratorСкачать  Виды треугольников по видам угловСкачать  7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать  Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать  Виды треугольников по углам.Скачать  Виды треугольниковСкачать  |
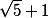 то вот в запросе пишем a=1;b=3;c=sqrt(5)+1
то вот в запросе пишем a=1;b=3;c=sqrt(5)+1 .
.




 .
. Найти
Найти 
 .
.
 .
. ,
,  .
.


 .
. .
. .
. и
и  (Рис.2). Найти сторону c и углы A и B.
(Рис.2). Найти сторону c и углы A и B.

 .
.

 .
.
 .
.
 .
. ,
,  .
. ,
,  .
. и углы
и углы  (Рис.3). Найти стороны b и c и угол С.
(Рис.3). Найти стороны b и c и угол С.


