Противолежащий катет — одно из важнейших понятий прямоугольного треугольника, на которое опирается определение синуса, тангенса и котангенса и которое широко используется при решении различных геометрических задач.
Один и тот же катет может выступать как в роли противолежащего, так и в роли прилежащего катета. Все зависит от того, по отношению к какому углу он рассматривается.
Как определить противолежащий катет?
Само название — противо лежащий — подсказывает его расположение.
Противолежащий катет — это катет, который лежит напротив данного угла.
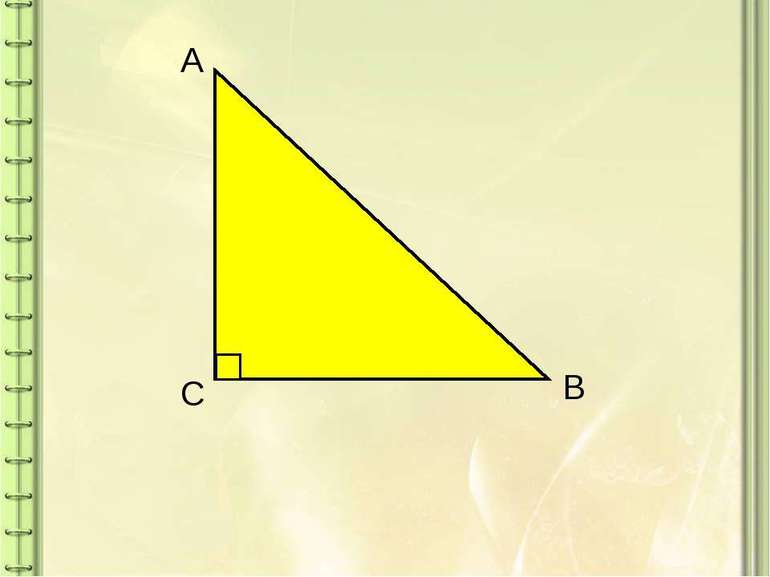
в треугольнике ABC
катет, противолежащий углу A
В этом же треугольнике ABC
катет, противолежащий углу C
Найти противолежащий катет поможет такая подсказка:
в названии катета, противолежащего данному углу, нет буквы, по которой назван этот угол.
(угол — A, противолежащий катет — BC. В названии BC нет буквы A;
угол — C, противолежащий катет — AB. В названии AB нет буквы С).
Одна из букв в названии противолежащего катета — «имя» прямого угла (в приведенных выше примерах — это B).
Противолежащий катет обязательно лежит напротив острого угла. Напротив прямого угла лежит гипотенуза!
Видео:Катеты и гипотенузаСкачать
Прямоугольный треугольник
Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).
Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.
Стороны, прилежащие к прямому углу, называются катетами .
Признаки равенства прямоугольных треугольников
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).
Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).
Свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна 90˚.
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.
И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.
3. Теорема Пифагора:
, где 
– катеты, 
– гипотенуза. Видеодоказательство
4. Площадь 
прямоугольного треугольника с катетами :
5. Высота 
прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:
6. Центр описанной окружности – есть середина гипотенузы.
7. Радиус 
описанной окружности есть половина гипотенузы :
8. Медиана, проведенная к гипотенузе, равна ее половине
9. Радиус 
вписанной окружности выражается через катеты и гипотенузу следующим образом:
Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.
Видео:7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать
Противолежащий катет в прямоугольном треугольнике — определение, формулы и задачи
Видео:Лайфхак нахождения катета в прямоугольном треугольникеСкачать
Основные понятия
Прямоугольным треугольником называется геометрическая фигура, состоящая из трех точек и отрезков, которые их соединяют. При этом один из углов обязательно равен 90°.
Чтобы точно знать, как определить противолежащий и прилежащий катеты, стоит запомнить утверждение: противолежащая сторона в прямоугольном треугольнике — это часть фигуры, которая размещена напротив этого угла, другая же будет прилежащей к гипотенузе. Отличить их очень просто: к примеру, в треугольнике ABC катетом, противолежащим ∠А, будет сторона ВС. По отношению к ∠С им станет АВ. Важное свойство: если противолежащий угол равен 30°, то катет будет равняться половине гипотенузы.
Чтобы легко понять размещение, стоит запомнить утверждение: в названии стороны, что находится напротив определенного угла, нет буквы, которая его обозначает. Он всегда будет острым, поскольку напротив 90° находится гипотенуза.
Слово «катет» имеет греческое происхождение. Оно переводится как «перпендикуляр», «опущенный», «отвесной». Это название распространено в архитектуре, здесь оно имеет значение отвеса, который опускают через середину задка ионической капители.
Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать
Катет в тригонометрии
Длину сторон можно найти, обратившись к тригонометрии. Синусом острого угла в прямоугольном треугольнике является отношение противоположного катета к гипотенузе. Выражается это утверждение так: sin А = a/с.
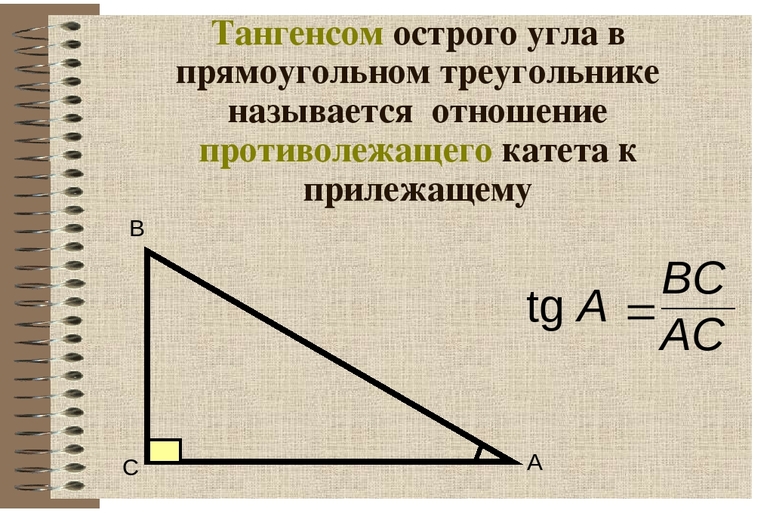
Косинус — отношение противоположного угла к гипотенузе. Это выражение описывается формулой cos А = b/с. Тангенс — отношение противолежащего катета к прилежащему, что можно записать следующим образом: tg А = а/b.
Видео:Известна площадь прямоугольного треугольника и один из острых углов. Найти противолежащий катетСкачать
Решение задач
Для решения задач часто используются понятия синус, косинус и тангенс. Здесь нужно руководствоваться формулой с = a/sin а = b/sin b, где c — гипотенуза, а и b — катеты, противоположные определенным углам. Если в задаче требуется найти сторону, то формула имеет другой вид:
Используя тригонометрическое значение угла (тангенс), для нахождения противолежащей стороны применяют формулы a = b/tg b и b = a/tg a. Часто в заданиях используют углы 30, 45, 60 и 90°, поэтому для практического использования стоит запомнить их тригонометрическое значение. Решение задач происходит по алгоритму, который включает следующие действия:
- Следует проанализировать фигуру, вычислить в ней сторону либо угол.
- Далее нужно подумать, как элементы треугольника связаны с тригонометрическими функциями либо между собой.
В конце приступают к решению, то есть записывают соотношение известных понятий.
Пример задачи: есть треугольник АВС, где ∠С = 90°, sin А = 7/25, АВ = 5 см. Найти сторону АС. При решении нужно использовать формулу sin А = ВС/АВ = 7/25.
Введем длину единичного отрезка, которая равная х см, тогда BC = 7x, АВ = 25x. Используя теорему Пифагора, где c² = a² + b², получаем AC² = (25x)² — (7x)² = 24x.
По условию АВ = 5 см, то есть АВ = 25х = 5, тогда х = 1/5. Если х = 1/5, то АС = 24/5 = 4,8 см.
Таким образом, изучая материал о прямоугольных треугольниках, ученики знакомятся с катетами и их свойствами. Они учатся решать задания, используя различные понятия либо комбинируя приобретенные ранее знания с новой темой.
🌟 Видео
Теорема Пифагора для чайников)))Скачать
№594. В прямоугольном треугольнике один из катетов равен b, а противолежащий угол равен β.Скачать
ПРИЛЕЖАЩИЙ КАТЕТ, КАК ТЕБЯ НАЙТИ?Скачать
№485. Найдите катет прямоугольного треугольника, лежащий против угла 60°, если гипотенуза равна с.Скачать
Нахождение стороны прямоугольного треугольникаСкачать
Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать
SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать
Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать
Как просто запомнить, что такое sin, cos, tg?! #косинус #синус #тангенс #математика #огэ #егэСкачать
Нахождение катета прямоугольного треугольникаСкачать
Определение длины гипотенузыСкачать
Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать
Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать
Что такое синус, косинус и тангенс угла в прямоугольном треугольнике. Часть 1Скачать
№256. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего из катетовСкачать
