Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Свойства острых углов в прямоугольном треугольнике
Острый угол в прямоугольном треугольнике — угол,
градусная мера которого менее 90º.
- Если известны 2 угла: чтобы найти острый угол надо из 90º
вычесть известный угол. - Катет прямоугольного треугольника, лежащий против острого угла в 30º,
равен половине гипотенузы. - Если в прямоугольном треугольнике острые углы равны, значит и катеты равны.
Видео:«Жертвоприношение. Часть 1: Треугольник смерти» | Путинизм как он есть #19Скачать

Как найти острый угол в прямоугольном треугольнике
- Если известны 2 угла: чтобы найти острый угол надо из 90º
вычесть известный угол. - Если известны катет a и катет b: чтобы найти острый угол надо
использовать формулу тангенса. - Если известна гипотенуза c и катет a: чтобы найти острый угол надо
использовать формулу синуса. - Если известна гипотенуза c и катет b: чтобы найти острый угол надо
использовать формулу косинуса.
Видео:«Жертвоприношение. Часть 1: Треугольник смерти» (версия 18+) | Путинизм как он есть #19Скачать

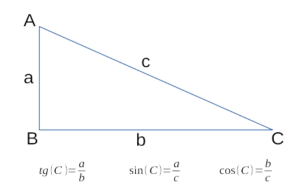
Определение синуса, косинуса, и тангенса острого угла прямоугольного треугольника
Синусом острого угла прямоугольного треугольника называется
отношение противолежащего этому углу катета к гипотенузе.
Косинусом острого угла прямоугольного треугольника называется
отношение прилежащего к этому углу катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называется
отношение противолежащего этому углу катета к прилежащему катету.
Видео:Найдите углы прямоугольного треугольника, если его гипотенуза равна 12, а площадь равна 18Скачать

Острый угол
Острый угол — это угол, меньший прямого.
Градусная мера острого угла больше нуля, но меньше 90 градусов.
∠ABC, ∠MNK, ∠DEF — острые углы.
Чтобы построить острый угол заданной градусной меры, пользуются транспортиром.
Построить с помощью транспортира угол 72º.
1) Отмечаем точку — вершину угла.
2) От точки проводим луч — сторону угла.
3) Совмещаем вершину угла с отметкой в центре транспортира (у разных моделей транспортира положение этой отметки может быть разным) так, чтобы отметка 0º была расположена на стороне угла.
4) Находим 72º на той шкале, где находится 0º, и ставим точку.
5) От вершины угла через отмеченную точку проводим луч — вторую сторону угла.
На рисунках изображено построение угла 72º с началом отсчёта по нижней шкале и с началом отсчёта по верхней шкале.
∠ABC=72º
∠CDE=72º
Чтобы определить по рисунку, является ли угол острым, можно воспользоваться угольником. Если приложить вершину угольника к вершине угла так, чтобы сторона угольника прошла через одну сторону угла, то другая сторона угольника закроет вторую сторону угла:
Видео:8 класс, 29 урок, Синус, косинус и тангенс острого угла прямоугольного треугольникаСкачать

Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂
Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается . Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .
Угол обозначается соответствующей греческой буквой .
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет , лежащий напротив угла , называется противолежащим (по отношению к углу ). Другой катет , который лежит на одной из сторон угла , называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.
Давайте докажем некоторые из них.
- Сумма углов любого треугольника равна . Значит, сумма двух острых углов прямоугольного треугольника равнa .
- С одной стороны, как отношение противолежащего катета к гипотенузе. С другой стороны, , поскольку для угла катет а будет прилежащим.Получаем, что . Иными словами, .
- Возьмем теорему Пифагора: . Поделим обе части на : Мы получили основное тригонометрическое тождество.
- Поделив обе части основного тригонометрического тождества на , получим: Это значит, что если нам дан тангенс острого угла , то мы сразу можем найти его косинус. Аналогично,
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Мы знаем, что сумма углов любого треугольника равна .
Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до .
| 0 | |
| 0 | |
| 0 | |
| 0 | − |
| − | 0 |
Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Ты нашел то, что искал? Поделись с друзьями!
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
1. В треугольнике угол равен , . Найдите .
Задача решается за четыре секунды.
2 . В треугольнике угол равен , , . Найдите .
Найдем по теореме Пифагора.
Часто в задачах встречаются треугольники с углами и или с углами и . Основные соотношения для них запоминайте наизусть!
Для треугольника с углами и катет, лежащий напротив угла в , равен половине гипотенузы.
Треугольник с углами и — равнобедренный. В нем гипотенуза в раз больше катета.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
🔥 Видео
Геометрия. 8 класс. Тригонометрические функции острого угла в прямоугольном треугольнике/17.11.2020/Скачать

Треугольники: остро-, тупо- и прямоугольныеСкачать

Математика 2 класс (Урок№33 - Угол. Виды углов: прямой, острый, тупой.)Скачать

Сравнение углов. Виды углов. Чертежный треугольник. 5 класс.Скачать

Урок СИНУС, КОСИНУС И ТАНГЕНС ОСТРОГО УГЛА ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКАСкачать

Найдите площадь прямоугольного треугольника с острым углом 15° и гипотенузой равной 4Скачать

ТРИГОНОМЕТРИЯ с нуля — Синус, косинус, тангенс и котангенс острого углаСкачать

Геометрия. 8 класс. Тригонометрические функции острого угла в прямоугольном треугольнике/19.11.2020/Скачать

#63. Задание 6: прямоугольный треугольникСкачать

ЕГЭ база #15 / Треугольники и их элементы / Угол между биссектрисой, медианой и высотой / решу егэСкачать

КАК НАЙТИ КОСИНУС ОСТРОГО УГЛА ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА? ОПРЕДЕЛЕНИЕ. ЗАДАЧА | ГЕОМЕТРИЯ 8 классСкачать

Геометрия. 8 класс. Тригонометрические функции острого угла в прямоугольном треугольникеСкачать

Синус, косинус и тангенс острого угла в прямоугольном треугольникеСкачать