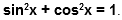Где находится п 12 на числовой окружности

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Как обозначать числа с пи на числовой окружности?

Надеюсь, вы уже прочитали про числовую окружность и знаете, почему она называется числовой, где на ней начало координат и в какой стороне положительное направление. Если нет, то бегом читать ! Если вы, конечно, собираетесь находить точки на числовой окружности.

Видео:10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

Обозначаем числа (2π), (π), (frac ), (-frac ), (frac )

Как вы знаете из прошлой статьи, радиус числовой окружности равен (1). Значит, длина окружности равняется (2π) (вычислили по формуле (l=2πR)). С учетом этого отметим (2π) на числовой окружности. Чтобы отметить это число нужно пройти от (0) по числовой окружности расстояние равно (2π) в положительном направлении, а так как длина окружности (2π), то получается, что мы сделаем полный оборот. То есть, числу (2π) и (0) соответствует одна и та же точка. Не переживайте, несколько значений для одной точки — это нормально для числовой окружности.

Теперь обозначим на числовой окружности число (π). (π) – это половина от (2π). Таким образом, чтобы отметить это число и соответствующую ему точку, нужно пройти от (0) в положительном направлении половину окружности.

Отметим точку (frac ) . (frac ) – это половина от (π), следовательно чтобы отметить это число, нужно от (0) пройти в положительном направлении расстояние равное половине (π), то есть четверть окружности.

Обозначим на окружности точки (-) (frac ) . Двигаемся на такое же расстояние, как в прошлый раз, но в отрицательном направлении.

Нанесем (-π). Для этого пройдем расстояние равное половине окружности в отрицательном направлении.

Теперь рассмотрим пример посложнее. Отметим на окружности число (frac ) . Для этого дробь (frac ) переведем в смешанный вид (frac ) (=1) (frac ) , т.е. (frac ) (=π+) (frac ) . Значит, нужно от (0) в положительную сторону пройти расстояние в пол окружности и еще в четверть.

Задание 1. Отметьте на числовой окружности точки (-2π),(-) (frac ) .

Видео:Как искать точки на тригонометрической окружности.Скачать

Обозначаем числа (frac ), (frac ), (frac )

Выше мы нашли значения в точках пересечения числовой окружности с осями (x) и (y). Теперь определим положение промежуточных точек. Для начала нанесем точки (frac ) , (frac ) и (frac ) .
(frac ) – это половина от (frac ) (то есть, (frac ) (=) (frac ) (:2)) , поэтому расстояние (frac ) – это половина четверти окружности.

(frac ) – это треть от (π) (иначе говоря, (frac ) (=π:3)), поэтому расстояние (frac ) – это треть от полукруга.

(frac ) – это половина (frac ) (ведь (frac ) (=) (frac ) (:2)) поэтому расстояние (frac ) – это половина от расстояния (frac ) .

Вот так они расположены друг относительно друга:

Замечание: Расположение точек со значением (0), (frac ) ,(π), (frac ) , (frac ) , (frac ) , (frac ) лучше просто запомнить. Без них числовая окружность, как компьютер без монитора, вроде бы и полезная штука, а использовать крайне неудобно.

Разные расстояние на окружности наглядно:

Видео:Длина дуги числовой окружности | Алгебра 10 класс #9 | ИнфоурокСкачать

Обозначаем числа (frac ), (-frac ), (frac )

Обозначим на окружности точку (frac ) , для этого выполним следующие преобразования: (frac ) (=) (frac ) (=) (frac ) (+) (frac ) (=π+) (frac ) . Отсюда видно, что от нуля в положительную сторону надо пройти расстояние (π), а потом еще (frac ) .

Отметим на окружности точку (-) (frac ) . Преобразовываем: (-) (frac ) (=-) (frac ) (-) (frac ) (=-π-) (frac ) . Значит надо от (0) пройти в отрицательную сторону расстояние (π) и еще (frac ) .

Нанесем точку (frac ) , для этого преобразуем (frac ) (=) (frac ) (=) (frac ) (-) (frac ) (=2π-) (frac ) . Значит, чтобы поставить точку со значением (frac ) , надо от точки со значением (2π) пройти в отрицательную сторону расстояние (frac ) .

Видео:Соответствие чисел точкам числовой окружностиСкачать

Обозначаем числа (10π), (-3π), (frac ) ,(frac ), (-frac ), (-frac )

Запишем (10π) в виде (5 cdot 2π). Вспоминаем, что (2π) – это расстояние равное длине окружности, поэтому чтобы отметить точку (10π), нужно от нуля пройти расстояние равное (5) окружностям. Нетрудно догадаться, что мы окажемся снова в точке (0), просто сделаем пять оборотов.

Из этого примера можно сделать вывод:

Числам с разницей в (2πn), где (n∈Z) (то есть (n) — любое целое число) соответствует одна и та же точка.

То есть, чтобы поставить число со значением больше (2π) (или меньше (-2π)), надо выделить из него целое четное количество (π) ((2π), (8π), (-10π)…) и отбросить. Тем самым мы уберем из числа, не влияющие на положение точки «пустые обороты».

Точке, которой соответствует (0), также соответствуют все четные количества (π) ((±2π),(±4π),(±6π)…).

Теперь нанесем на окружность (-3π). (-3π=-π-2π), значит (-3π) и (–π) находятся в одном месте на окружности (так как отличаются на «пустой оборот» в (-2π)).

Кстати, там же будут находиться все нечетные (π).

Точке, которой соответствует (π), также соответствуют все нечетные количества (π) ((±π),(±3π),(±5π)…).

Сейчас обозначим число (frac ) . Как обычно, преобразовываем: (frac ) (=) (frac ) (+) (frac ) (=3π+) (frac ) (=2π+π+) (frac ) . Два пи – отбрасываем, и получается что, для обозначения числа (frac ) нужно от нуля в положительную сторону пройти расстояние равное (π+) (frac ) (т.е. половину окружности и еще четверть).

Отметим (frac ) . Вновь преобразования: (frac ) (=) (frac ) (=) (frac ) (+) (frac ) (=5π+) (frac ) (=4π+π+) (frac ) . Ясно, что от нуля надо пройти расстояние равное (π+) (frac ) – и мы найдем место точки (frac ) .

Нанесем на окружность число (-) (frac ) .
(-) (frac ) (= -) (frac ) (-) (frac ) (=-10π-) (frac ) . Значит, место (-) (frac ) совпадает с местом числа (-) (frac ) .

Обозначим (-) (frac ) .
(-) (frac ) (=-) (frac ) (+) (frac ) (=-5π+) (frac ) (=-4π-π+) (frac ) . Для обозначение (-) (frac ) , на числовой окружности надо от точки со значением (–π) пройти в положительную сторону (frac ) .

Видео:Как найти координаты точек на тригонометрической окружностиСкачать

Точка пи / 12 где находиться на тригонометрической окружности?

Математика | 10 — 11 классы

Точка пи / 12 где находиться на тригонометрической окружности.

π / 12 = 180 / 12 = 15°

пояснение на картинке.

Видео:Алгебра 10 класс. 20 сентября. Числовая окружность #6 координаты точекСкачать

Диаметр окружности равен 12 см?

Диаметр окружности равен 12 см.

Какое расстояние может быть от центра этой окружности до точки, чтобы эта точка находилась внутри окружности?

Видео:Точки на числовой окружностиСкачать

Число 3п соответствует точке тригонометрической окружности с ординатой ?

Число 3п соответствует точке тригонометрической окружности с ординатой ?

Видео:Задание №13. Как отбирать корни в тригонометрической окружности? 🤔Скачать

Начертите окружность с центром в точке О и радиусом 3 см 5 мм?

Начертите окружность с центром в точке О и радиусом 3 см 5 мм.

Проведите прямую, которая пересекает окружность в точках М и К.

На каком расстояние от центра окружности находятся эти точки?

Видео:Определение значений по точкам на числовой окружностиСкачать

Начерти окружность с центром О и радиус 3 см 5 мм?

Начерти окружность с центром О и радиус 3 см 5 мм.

Проведите прямую, которая пересекает окружность в точках М и К, На каком расстоянии от центра окружности находятся эти точки?

Видео:Числовая окружностьСкачать

Отметь красным цветом точки которые находятся на окружности с центром в точке О?

Отметь красным цветом точки которые находятся на окружности с центром в точке О.

Видео:Промежутки на числовой окружностиСкачать

Подскажите где на окружности находятся точки [0 ; 2pi]?

Подскажите где на окружности находятся точки [0 ; 2pi].

Видео:Тригонометрическая окружность. Как выучить?Скачать

Вася сказал, что окружность это геометрическая фигура все точки которой находятся на одинаковом расстоянии от данной точки, а Валя сказала что такая фигура — не обязательно окружность?

Вася сказал, что окружность это геометрическая фигура все точки которой находятся на одинаковом расстоянии от данной точки, а Валя сказала что такая фигура — не обязательно окружность.

Кто из них прав?

Видео:Отбор корней по окружностиСкачать

Где находится на числовой окружности точка — пи / 12?

Где находится на числовой окружности точка — пи / 12.

Видео:Отбор корней по окружностиСкачать

Отметьте в тетради точку о?

Отметьте в тетради точку о.

Постройте окружность с центром в этой точке.

Измерь радиус окружности.

Чему равен диаметр.

Объясните пожалусто как диаметр находить))).

Видео:Алгебра 10 класс. 15 сентября. Числовая окружность #1Скачать

Нарисуй две окружности радиусом 3 см, чтобы они пересекались?

Нарисуй две окружности радиусом 3 см, чтобы они пересекались.

Отметь точки, которые принадлежат обеим окружностям.

Отметь точку, которая находится внутри обеих окружностей.

Сколько таких точек?

На этой странице сайта размещен вопрос Точка пи / 12 где находиться на тригонометрической окружности? из категории Математика с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 10 — 11 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

56•60 = 3360 секунд 56 я умножаю на 60 секунд вот тебе ответ 3360.

(1 00 + 80 : 5) : 2 = 58 ((100 — 80) * 5) : 2 = 50.

Делители числа 12 это числа : 12, 6, 4, 3, 2, 1. Эти точки и нужно изобразить на координатном луче.

Видео:Урок 1.3 Как расставлять точки на числовой окружности?Скачать

Единичная окружность

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Деление окружности на 12 равных частейСкачать

Единичная окружность в тригонометрии

Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.

Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.

Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.

Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.

Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.

Поясним, как единичная окружность связана с тригонометрией.

В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.

Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.

Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.

Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:

• Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
• Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
• В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
• В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.

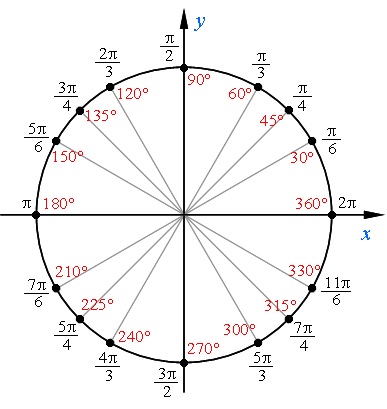
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:

Радиан — одна из мер для определения величины угла.

Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.

Число радиан для полной окружности — 360 градусов.

Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.

Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.

Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:

• 2π радиан = 360°
• 1 радиан = (360/2π) градусов
• 1 радиан = (180/π) градусов
• 360° = 2π радиан
• 1° = (2π/360) радиан
• 1° = (π/180) радиан

Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.

Уравнение единичной окружности

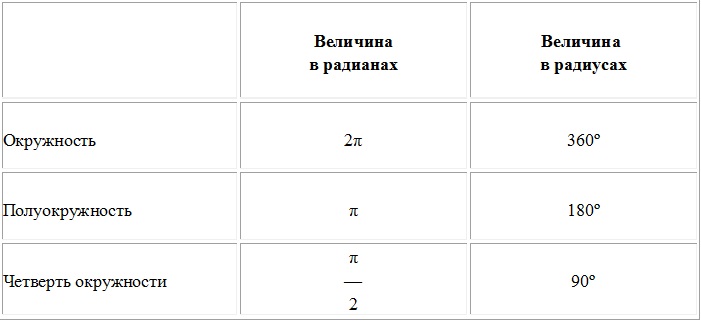
При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Видео:Координаты точек на числовой окружности, часть 5. Алгебра 10 класс.Скачать

Где находится п 12 на числовой окружности

Единичной окружностью называют окружность радиуса 1.

Числовая окружность — это единичная окружность, точки которой соответствуют определенным действительным числам.

Отсчет по числовой окружности может вестись как по часовой стрелке, так и против часовой стрелки. Отсчет от точки А против часовой стрелки называется положительным направлением. Отсчет от точки А по часовой стрелке называется отрицательным направлением.

Центр радиуса числовой окружности соответствует началу координат (числу 0). Горизонтальный диаметр соответствует оси x, вертикальный — оси y. Начальная точка А числовой окружности находится на оси x и имеет координаты (1; 0).

Любая точка числовой окружности с координатами (x; y) не может быть меньше -1, но не может быть больше 1:&nbsp ;&nbsp

Есть несколько простых закономерностей, которые помогут вам легко запомнить основные имена числовой окружности. Перед тем как начать, напомним: отсчет ведется в положительном направлении, то есть от точки А (2П) против часовой стрелки.

1) Начнем с крайних точек на осях координат. Начальная точка — это 2П (крайняя правая точка на оси х, равная 1). Как вы знаете, 2П — это длина окружности. Значит, половина окружности — это 1П или П. Ось х делит окружность как раз пополам. Соответственно, крайняя левая точка на оси х, равная -1, называется П. Крайняя верхняя точка на оси у, равная 1, делит верхнюю полуокружность пополам. Значит, если полуокружность — это П, то половина полуокружности — это П/2. Одновременно П/2 — это и четверть окружности. Отсчитаем три таких четверти от первой до третьей — и мы придем в крайнюю нижнюю точку на оси у, равной -1. Но если она включает три четверти — значит имя ей 3П/2.

Определение. Если точка М числовой окружности соответствует числу t, то абсциссу точки М называют косинусом числа t и обозначают соs t, а ординату точки М называют синусом числа t и обозначают sin t.
Если М(t) = М(х;у), то х = cost, у = sint.

Определение. Отношение синуса числа t к косинусу того же числа называют тангенсом числа t. Отношение косинуса числа t к синусу того же числа называют котангенсом числа t.

Видео:РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Где находится п 12 на числовой окружности

Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам.

Единичной окружностью называют окружность радиуса 1.

Общий вид числовой окружности.

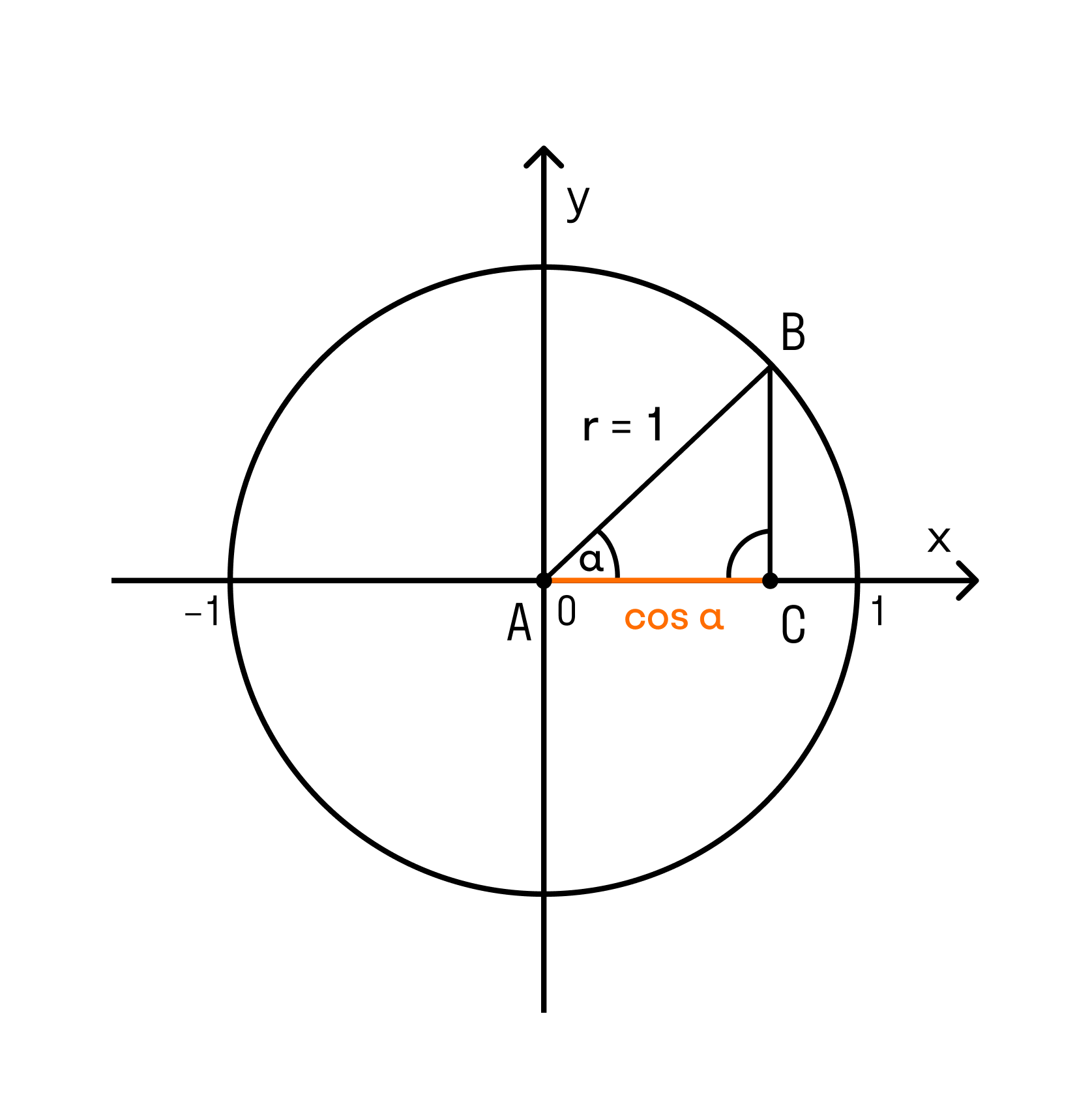
1) Ее радиус принимается за единицу измерения.

2) Горизонтальный и вертикальный диаметры делят числовую окружность на четыре четверти (см.рисунок). Их соответственно называют первой, второй, третьей и четвертой четвертью.

3) Горизонтальный диаметр обозначают AC, причем А – это крайняя правая точка.
Вертикальный диаметр обозначают BD, причем B – это крайняя верхняя точка.
Соответственно:

первая четверть – это дуга AB

вторая четверть – дуга BC

третья четверть – дуга CD

четвертая четверть – дуга DA

4) Начальная точка числовой окружности – точка А.

Отсчет по числовой окружности может вестись как по часовой стрелке, так и против часовой стрелки.
Отсчет от точки А против часовой стрелки называется положительным направлением.
Отсчет от точки А по часовой стрелке называется отрицательным направлением.

Числовая окружность на координатной плоскости.

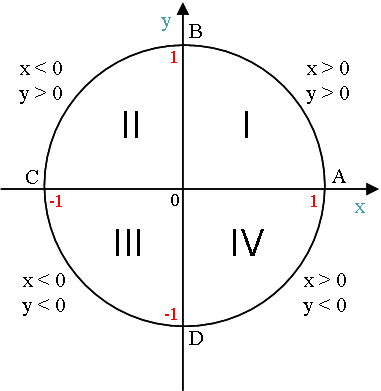
Центр радиуса числовой окружности соответствует началу координат (числу 0).

Горизонтальный диаметр соответствует оси x, вертикальный – оси y.

Начальная точка А числовой окружности находится на оси x и имеет координаты (1; 0).

Значения x и y в четвертях числовой окружности:

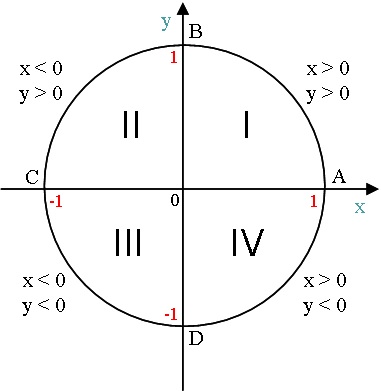
x 0, y Основные величины числовой окружности:

Величина
в радианах

Величина
в радиусах

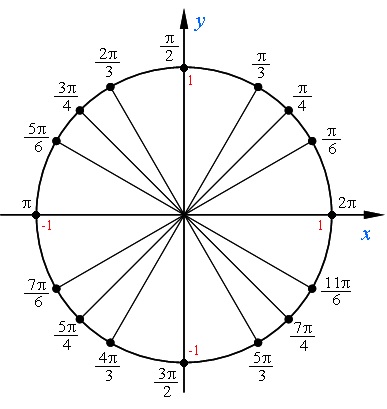
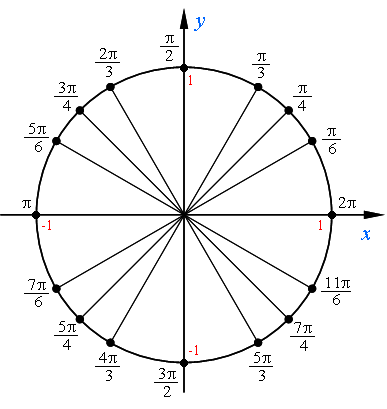
Имена и местонахождение основных точек числовой окружности:

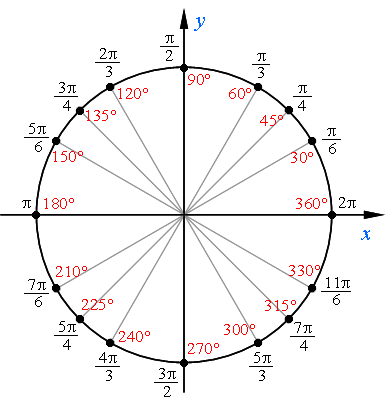
Как запомнить имена числовой окружности.

Есть несколько простых закономерностей, которые помогут вам легко запомнить основные имена числовой окружности.

Перед тем как начать, напомним: отсчет ведется в положительном направлении, то есть от точки А (2π) против часовой стрелки.

1) Начнем с крайних точек на осях координат.

Начальная точка – это 2π (крайняя правая точка на оси х, равная 1).

Как вы знаете, 2π – это длина окружности. Значит, половина окружности – это 1π или π. Ось х делит окружность как раз пополам. Соответственно, крайняя левая точка на оси х, равная -1, называется π.

Крайняя верхняя точка на оси у, равная 1, делит верхнюю полуокружность пополам. Значит, если полуокружность – это π, то половина полуокружности – это π/2.

Одновременно π/2 – это и четверть окружности. Отсчитаем три таких четверти от первой до третьей – и мы придем в крайнюю нижнюю точку на оси у, равной -1. Но если она включает три четверти – значит имя ей 3π/2.

2) Теперь перейдем к остальным точкам. Обратите внимание: все противоположные точки имеют одинаковый числитель – причем это противоположные точки и относительно оси у, и относительно центра осей, и относительно оси х. Это нам и поможет знать их значения точек без зубрежки.

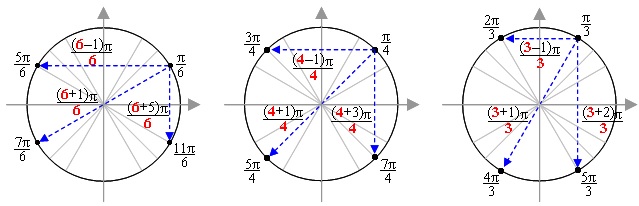
Надо запомнить лишь значение точек первой четверти: π/6, π/4 и π/3. И тогда мы «увидим» некоторые закономерности:

— Относительно оси у в точках второй четверти, противоположных точкам первой четверти, числа в числителях на 1 меньше величины знаменателей. К примеру, возьмем точку π/6. Противоположная ей точка относительно оси у тоже в знаменателе имеет 6, а в числителе 5 (на 1 меньше). То есть имя этой точки: 5π/6. Точка, противоположная π/4, тоже имеет в знаменателе 4, а в числителе 3 (на 1 меньше, чем 4) – то есть это точка 3π/4.
Точка, противоположная π/3, тоже имеет в знаменателе 3, а в числителе на 1 меньше: 2π/3.

— Относительно центра осей координат все наоборот: числа в числителях противоположных точек (в третьей четверти) на 1 больше значения знаменателей. Возьмем опять точку π/6. Противоположная ей относительно центра точка тоже имеет в знаменателе 6, а в числителе число на 1 больше – то есть это 7π/6.

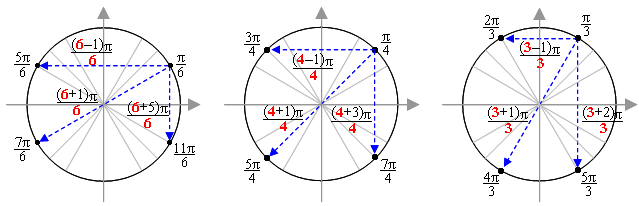
Точка, противоположная точке π/4, тоже имеет в знаменателе 4, а в числителе число на 1 больше: 5π/4.
Точка, противоположная точке π/3, тоже имеет в знаменателе 3, а в числителе число на 1 больше: 4π/3.

— Относительно оси х (четвертая четверть) дело посложнее. Здесь надо к величине знаменателя прибавить число, которое на 1 меньше – эта сумма и будет равна числовой части числителя противоположной точки. Начнем опять с π/6. Прибавим к величине знаменателя, равной 6, число, которое на 1 меньше этого числа – то есть 5. Получаем: 6 + 5 = 11. Значит, противоположная ей относительно оси х точка будет иметь в знаменателе 6, а в числителе 11 – то есть 11π/6.

Точка π/4. Прибавляем к величине знаменателя число на 1 меньше: 4 + 3 = 7. Значит, противоположная ей относительно оси х точка имеет в знаменателе 4, а в числителе 7 – то есть 7π/4.
Точка π/3. Знаменатель равен 3. Прибавляем к 3 на единицу меньшее число – то есть 2. Получаем 5. Значит, противоположная ей точка имеет в числителе 5 – и это точка 5π/3.

3) Еще одна закономерность для точек середин четвертей. Понятно, что их знаменатель равен 4. Обратим внимание на числители. Числитель середины первой четверти – это 1π (но 1 не принято писать). Числитель середины второй четверти – это 3π. Числитель середины третьей четверти – это 5π. Числитель середины четвертой четверти – это 7π. Получается, что в числителях середин четвертей – четыре первых нечетных числа в порядке их возрастания:
(1)π, 3π, 5π, 7π.
Это тоже очень просто. Поскольку середины всех четвертей имеют в знаменателе 4, то мы уже знаем их полные имена: π/4, 3π/4, 5π/4, 7π/4.

Особенности числовой окружности. Сравнение с числовой прямой.

Как вы знаете, на числовой прямой каждая точка соответствует единственному числу. К примеру, если точка А на прямой равна 3, то она уже не может равняться никакому другому числу.

На числовой окружности все иначе, поскольку это окружность. К примеру, чтобы из точки А окружности прийти к точке M, можно сделать это, как на прямой (только пройдя дугу), а можно и обогнуть целый круг, а потом уже прийти к точке M. Вывод:

Пусть точка M равна какому-то числу t. Как мы знаем, длина окружности равна 2π. Значит, точку окружности t мы можем записать двояко: t или t + 2π. Это равнозначные величины.
То есть t = t + 2π. Разница лишь в том, что в первом случае вы пришли к точке M сразу, не делая круга, а во втором случае вы совершили круг, но в итоге оказались в той же точке M. Таких кругов можно сделать и два, и три, и двести. Если обозначить количество кругов буквой k, то получим новое выражение:
t = t + 2πk.

Отсюда формула:

Если точка M числовой окружности равна числу t, то она равна и числу вида t + 2πk, где k – любое целое число:

M(t) = M(t + 2πk),

где k ∈ Z.

Число k называется параметром.

Уравнение числовой окружности
(второе уравнение – в разделе «Синус, косинус, тангенс, котангенс»):