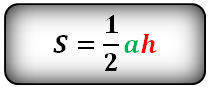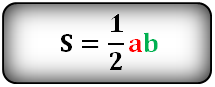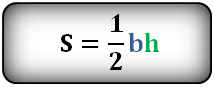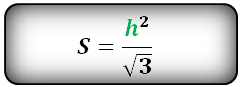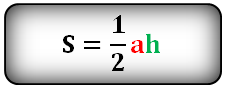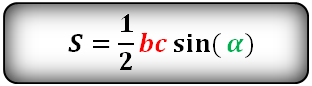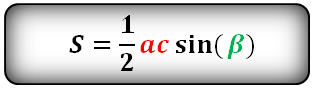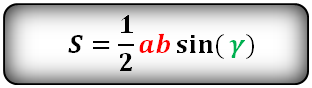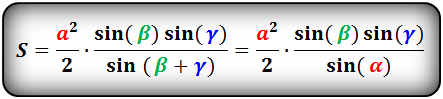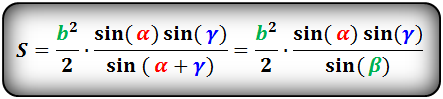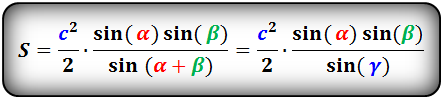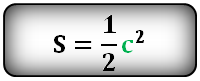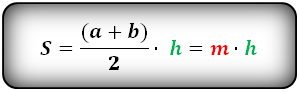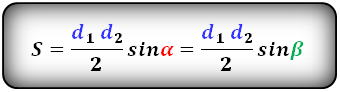- 1. Формула площади круга через радиус или диаметр
- 2. Формула расчета площади треугольника
- 3. Площадь треугольника, формула Герона
- 4. Площадь прямоугольного треугольника по катетам
- 5. Как вычислить площадь равнобедренного треугольника ?
- 6. Площадь равностороннего треугольника равна:
- 7. Найти площадь треугольника, угол и две стороны
- 8. Площадь треугольника по стороне и двум углам, формула.
- 9. Формула расчета площади прямоугольника
- 10. Как рассчитать площадь квадрата через диагональ или сторону
- 11. Формулы площади параллелограмма
- 12. Площадь произвольной трапеции
- 13. Площадь равнобедренной трапеции
- Формулы площадей фигур
- Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
- Формула площади треугольника по трем сторонам
- Формула площади треугольника по двум сторонам и углу между ними
- Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
- Формулы площади квадрата
- Формула площади квадрата по длине стороны
- Формула площади квадрата по длине диагонали
- Формула площади прямоугольника
- Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
- Формула площади параллелограмма по двум сторонам и углу между ними
- Формула площади параллелограмма по двум диагоналям и углу между ними
- Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
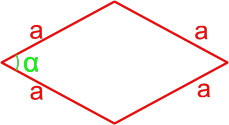
- Формула площади ромба по длине стороны и углу
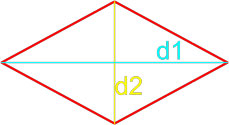
- Формула площади ромба по длинам его диагоналей
- Формулы площади трапеции
- Формула Герона для трапеции
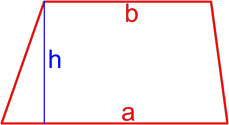
- Формула площади трапеции по длине основ и высоте
- Формулы площади дельтоида
- Формула площади дельтоида по двум неравным сторонам и углу между ними
- Формула площади дельтоида по равным сторонам и углу между ними
- Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности
- Формула площади дельтоида по двум диагоналям
- Формулы площади произвольного выпуклого четырехугольника
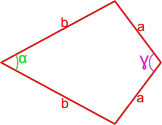
- Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними
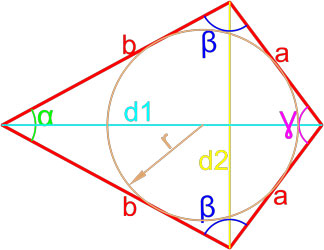
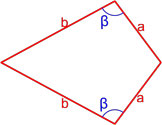
- Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов
- Формула площади вписанного четырехугольника (формула Брахмагупты)
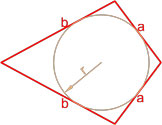
- Формула площади четырехугольника с вписанной окружностью
- Формула площади четырехугольника с вписанной и описанной окружностями
- Формулы площади круга
- Формула площади круга через радиус
- Формула площади круга через диаметр
- Площадь сегмента круга
- Площадь кругового сегмента через угол в градусах.
- Площадь кругового сегмента через угол в радианах.
- Формула площади эллипса
- Как найти площадь треугольника
- Основные понятия
- Формула площади треугольника
- Общая формула
- 1. Площадь треугольника через основание и высоту
- 2. Площадь треугольника через две стороны и угол между ними
- 3. Площадь треугольника через описанную окружность и стороны
- 4. Площадь треугольника через вписанную окружность и стороны
- 5. Площадь треугольника по стороне и двум прилежащим углам
- 6. Формула Герона для вычисления площади треугольника
- Для прямоугольного треугольника
- Площадь треугольника с углом 90° по двум сторонам
- Площадь треугольника по гипотенузе и острому углу
- Площадь прямоугольного треугольника по катету и прилежащему углу
- Площадь треугольника через гипотенузу и радиус вписанной окружности
- Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
- Площадь прямоугольного треугольника по формуле Герона
- Для равнобедренного треугольника
- Вычисление площади через основание и высоту
- Поиск площади через боковые стороны и угол между ними
- Площадь равностороннего треугольника через радиус описанной окружности
- Площадь равностороннего треугольника через радиус вписанной окружности
- Площадь равностороннего треугольника через сторону
- Площадь равностороннего треугольника через высоту
- Таблица формул нахождения площади треугольника
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

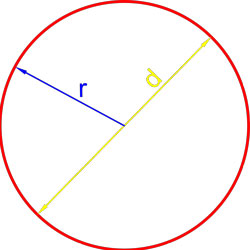
1. Формула площади круга через радиус или диаметр
Зная диаметр или радиус круга, можно найти его площадь.
r — радиус круга
D — диаметр
Формула площади круга, (S):
Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

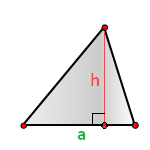
2. Формула расчета площади треугольника
h — высота треугольника
a — основание
Площадь треугольника (S):
Видео:Формулы площади треугольника. Вписаная и описаная окружностьСкачать

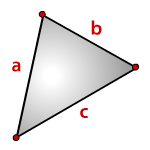
3. Площадь треугольника, формула Герона
a , b , c , — стороны треугольника
p— полупериметр, p=( a + b + c )/2
Формула ( Герона ) площади треугольника через полупериметр ( S ):
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

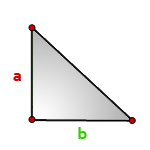
4. Площадь прямоугольного треугольника по катетам
Зная катеты прямоугольного треугольника, можно по формуле, найти его площадь.
a , b — катеты треугольника
Формула площади прямоугольного треугольника, (S):
Видео:Геометрия 9 класс (Урок№22 - Формулы площади правильного многоугольника,стороны и радиуса впис.окр.)Скачать

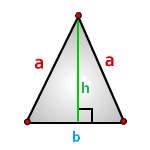
5. Как вычислить площадь равнобедренного треугольника ?
b — основание треугольника
a — равные стороны
h — высота
Формула площади треугольника через высоту h и основание b , ( S ):
Формула площади треугольника через, стороны a , b , (S):

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

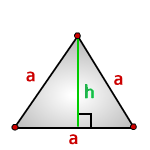
6. Площадь равностороннего треугольника равна:
Формулы расчета, площади равностороннего треугольника.
a — сторона треугольника
h — высота
Площадь треугольника только через сторону a , (S):
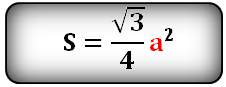
Площадь треугольника только через высоту h , ( S ):
Площадь треугольника через сторону a и высоту h , (S):
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

7. Найти площадь треугольника, угол и две стороны
Зная у треугольника, две стороны и синус угла между ними, находим по формуле, его площадь.
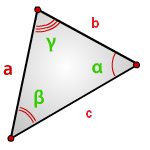
a , b , c — стороны треугольника
α , β , γ — углы
Формулы площади треугольника, через две стороны и угол между ними, ( S ):
Видео:Формулы радиусов описанной и вписанной окружностей правильного многоугольника 2Скачать

8. Площадь треугольника по стороне и двум углам, формула.
a , b , c — стороны треугольника
α , β , γ — противолежащие углы
Площадь треугольника через сторону и два угла (S):
Видео:Радиус вписанной окружности, формулу через площадь и полупериметрСкачать

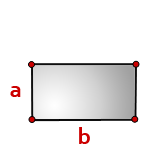
9. Формула расчета площади прямоугольника
b — длина прямоугольника
a — ширина
Формула площади прямоугольника, (S):
Видео:Радиус описанной окружностиСкачать

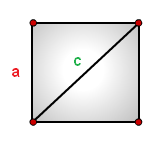
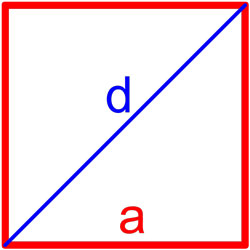
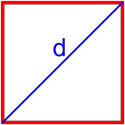
10. Как рассчитать площадь квадрата через диагональ или сторону
a — сторона квадрата
c — диагональ
Формула площади квадрата через сторону a , (S):
Формула площади квадрата через диагональ c , (S):
Видео:Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать

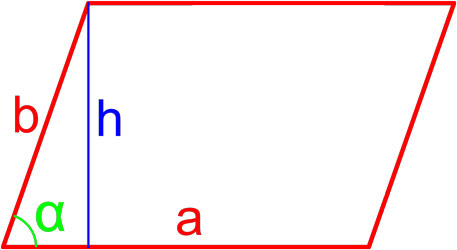
11. Формулы площади параллелограмма
1. Формула площади параллелограмма через стороны и углы
a, b — стороны параллелограмма
α , β — углы параллелограмма
Формула площади через стороны и углы параллелограмма, ( S ):
2. Формула площади параллелограмма через сторону и высоту
a, b — стороны параллелограмма
H b — высота на сторону b
H a — высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):
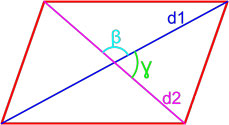
3. Формула площади параллелограмма через диагонали и угол между ними
D — большая диагональ
d — меньшая диагональ
α , β — углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):
Видео:112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписаннойСкачать

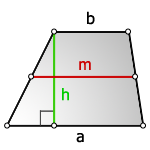
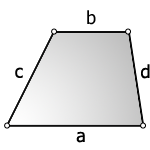
12. Площадь произвольной трапеции
1. Формула площади трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
m — средняя линия
h — высота трапеции
Формула площади трапеции, (S):
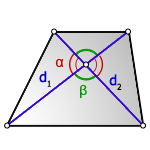
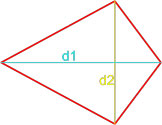
2. Формула площади трапеции через диагонали и угол между ними
d 1, d 2 — диагонали трапеции
α , β — углы между диагоналями
Формула площади трапеции, (S):
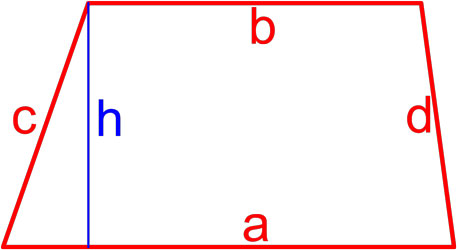
3. Формула площади трапеции через четыре стороны
b — верхнее основание
a — нижнее основание
c, d — боковые стороны
Формула площади трапеции, (S):
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

13. Площадь равнобедренной трапеции
1. Формула площади равнобедренной трапеции через стороны и угол
b — верхнее основание
a — нижнее основание
c — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобокой трапеции через радиус вписанной окружности
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α , β — углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α , β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
m — средняя линия трапеции
c — боковая сторона
α , β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Формулы площадей фигур
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Видео:Площадь треугольника через радиус вписанной и описанной окружности#огэматематикаСкачать

Формулы площади треугольника
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.
где a — одна из сторон треугольника, h — высота, проведенная к стороне треугольника.
Формула площади треугольника по трем сторонам
Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c .
S = p p — a p — b p — c ,
где p — полупериметр треугольника: p = a + b + c 2
a, b, c — стороны треугольника.
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
S = 1 2 a · b · sin γ ,
где a, b — стороны треугольника,
γ — угол между сторонами a и b .
Формула площади треугольника по трем сторонам и радиусу описанной окружности
a, b, c — стороны треугольника,
R — радиус описанной окружности.
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
где S — площадь треугольника,
r — радиус вписанной окружности,
p — полупериметр треугольника: p = a + b + c 2
Видео:Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать

Формулы площади квадрата
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.
где S — площадь квадрата,
a — длина стороны квадрата.
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.
где S — площадь квадрата,
d — длина диагонали квадрата.
Видео:Формула радиуса описанной окружности треугольника. Геометрия 9 классСкачать

Формула площади прямоугольника
Площадь прямоугольника равна произведению длин двух его смежных сторон.
где S — площадь прямоугольника,
a, b — длины сторон прямоугольника.
Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Формулы площади параллелограмма
Параллелограмм — это четырёхугольник, у которого противолежащие стороны параллельны.
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.
где S — площадь параллелограмма,
a, h — длины сторон параллелограмма.
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
где S — площадь параллелограмма,
a, b — длины сторон параллелограмма,
α — угол между сторонами параллелограмма.
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.
S = d1 · d2 · sin β 2 = d1 · d2 · sin γ 2 ,
где S — площадь параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
β , γ — угол между диагоналями параллелограмма.
Видео:Геометрия. 9 класс. Формулы для нахождения радиусов вписанной и описанной окружностей треугольникаСкачать

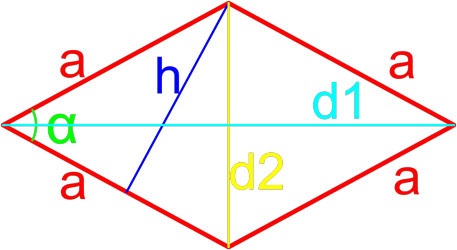
Формулы площади ромба
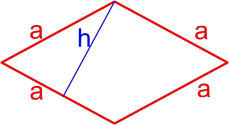
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
где S — площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба.
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
где S — площадь ромба,
a — длина стороны ромба,
α — угол между сторонами ромба.
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.
где S — площадь ромба,
d1, d2 — длины диагоналей ромба.
Видео:Теорема синусов и косинусов. Связь площади треугольника с радиусами вписанной и описанной окружностиСкачать

Формулы площади трапеции
Трапеция — это четырёхугольник, у которого две ( a, b ) стороны параллельны (основания), а две другие ( c, d ) стороны не параллельны (боковые стороны).
Формула Герона для трапеции
где S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,
p = a + b + c + d 2 — полупериметр трапеции.
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы её оснований на высоту.
где S — площадь трапеции,
a, b — длины основ трапеции,
h — высота трапеции.
Формулы площади дельтоида
Дельтоид — это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания.
Формула площади дельтоида по двум неравным сторонам и углу между ними
Площадь дельтоида равна произведению длин неравных сторон на синус угла между ними.
где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
β — угол между неравными сторонами дельтоида.
Формула площади дельтоида по равным сторонам и углу между ними
Площадь дельтоида равна полусумме произведения каждой из пар равных сторон на синус угла между ними.
S = a 2 sin γ + b 2 sin α 2 ,
где S — площадь дельтоида,
a, b — длины сторон дельтоида,
α — угол между равными сторонами b ,
γ — угол между равными сторонами a .
Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности
Площадь дельтоида равна произведению суммы неравных сторон на радиус вписанной окружности.
где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
r — радиус вписанной окружности.
Формула площади дельтоида по двум диагоналям
Площадь дельтоида равна половине произведения длин двух диагоналей.
где S — площадь дельтоида,
d1, d2 — диагонали дельтоида.
Формулы площади произвольного выпуклого четырехугольника
Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними
Площадь произвольного выпуклого выпуклого четырехугольника равна половине произведения его диагоналей умноженной на синус угла между ними.
S = d1 · d2 · sin γ 2 ,
где S — площадь четырехугольника,
d1, d2 — диагонали четырехугольника,
γ — любой из четырёх углов между диагоналями.
Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника,
θ = α + β 2 — полусумма двух противоположных углов четырехугольника.
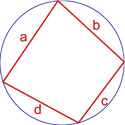
Формула площади вписанного четырехугольника (формула Брахмагупты)
Если вокруг четырехугольника можно описать окружность, то его площадь равна
S = p — a p — b p — c p — d ,
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника.
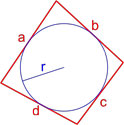
Формула площади четырехугольника с вписанной окружностью
Если в четырехугольник можно вписать окружность, то его площадь равна:
где S — площадь четырехугольника,
r — радиус вписанной окружности,
p = a + b + c + d 2 — полупериметр четырехугольника.
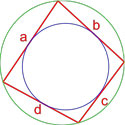
Формула площади четырехугольника с вписанной и описанной окружностями
Если в четырехугольник можно вписать окружность, а также около него можно описать окружность, то его площадь равна:
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника.
Формулы площади круга
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.
где S — площадь круга,
r — радиус круга.
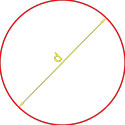
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.
где S — площадь круга,
d — диаметр круга.
Площадь сегмента круга
Площадь кругового сегмента через угол в градусах.
где S — площадь сегмента круга,
R — радиус круга,
α° — угол в градусах.
Площадь кругового сегмента через угол в радианах.
где S — площадь сегмента круга,
R — радиус круга,
α° — угол в радианах.
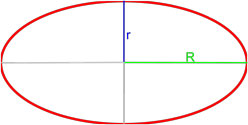
Формула площади эллипса
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.
где S — площадь эллипса,
a — длина большей полуоси эллипса,
b — длина меньшей полуоси эллипса.
Как найти площадь треугольника
О чем эта статья:
8 класс, 9 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.
Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!
Общая формула
1. Площадь треугольника через основание и высоту
, где — основание, — высота.
2. Площадь треугольника через две стороны и угол между ними
, где , — стороны, — угол между ними.
3. Площадь треугольника через описанную окружность и стороны
, где , , — стороны, — радиус описанной окружности.
4. Площадь треугольника через вписанную окружность и стороны
, где , , — стороны, — радиус вписанной окружности.
Если учитывать, что — это способ поиска полупериметра, то формулу можно записать следующим образом:
5. Площадь треугольника по стороне и двум прилежащим углам
, где — сторона, и — прилежащие углы.
6. Формула Герона для вычисления площади треугольника
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
, где , , — стороны, — полупериметр, который можно найти по формуле:
Для прямоугольного треугольника
Площадь треугольника с углом 90° по двум сторонам
Площадь треугольника по гипотенузе и острому углу
, где — гипотенуза, — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу
, где — катет, — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и радиус вписанной окружности
, где — гипотенуза, — радиус вписанной окружности.
Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
, где , — части гипотенузы.
Площадь прямоугольного треугольника по формуле Герона
, где , — катеты, — полупериметр, который можно найти по формуле:
Для равнобедренного треугольника
Вычисление площади через основание и высоту
, где — основание, — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними
, где — боковая сторона, — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности
, где — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности
, где — радиус вписанной окружности.
Площадь равностороннего треугольника через сторону
Площадь равностороннего треугольника через высоту
Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу, использовать как закладку в тетрадке или учебнике и обращаться к ней по необходимости.