Равносторонний треугольник — это самый простой правильный многоугольник из возможных. При нахождении его площади возникают частные варианты его расчета. Важно знать и понимать признаки и свойства этого вида фигур, для более легкого вычисления этого параметра. Все методы, представленные ниже, достаточно просты в применении, и не потребуют глубокого осмысления….
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Признаки и свойства фигуры
Для того чтобы рассчитать его площадь необходимо понимать свойства и признаки, которыми он обладает. Можно выделить следующие основные признаки этой фигуры:
- Значение величины его углов одинаково во всех случаях и равняется 60 градусам, вне зависимости от размера сторон.
- Биссектриса, высота и медиана выпущенные из одного угла будут совпадать.
- Любая сторона равностороннего треугольника равна двум другим.
- Центр правильного треугольника будет являться центром для вписанной и описанной окружности.
- Является частным случаем равнобедренного треугольника.
Важно! Если хотя бы один из этих признаков соблюдается, значит, треугольник является равносторонним. 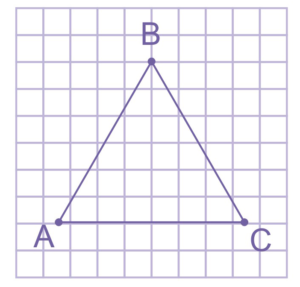
Дополнительно этот частный случай фигуры обладает следующими свойствами:
- Средняя линия, которая делит две боковые стороны пополам, равняется половине основания, параллельно которому она располагается.
- Сумма всех его углов не превышает 180 градусов.
- Радиус вписанной окружности рассчитывается по следующей формуле r =
, а описанной согласно выражению R =
.
- Радиус описанной окружности в правильном треугольнике в 2 раза больше радиуса вписанной.
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Расчет через сторону
Существует множество способов расчета площади этой фигуры. Все они имеют свои преимущества и недостатки. Применяются в зависимости от условий, представленных задаче. Самая популярный способ найти искомое значение для равностороннего треугольника вычисляется через произведение половины сторон и синуса угла между ними, выглядит это следующим образом: 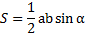
В случае с равносторонним, этот способ упрощается в значительной степени. Для этого нужно обратиться к рассмотренным выше признакам и свойствам. Исходя из того, что все углы этой фигуры равны, и равняются 60 градусам. Синус 60 градусов, согласно таблице Брадиса, равняется 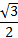
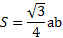
Учитывая то, что все стороны этой фигуры равны, то преобразованное выражение даст такой результат: 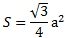
Данная формула отлично подойдет в случае, если известна величина стороны этой фигуры. В таком виде вычислять данный показатель гораздо легче и быстрее.
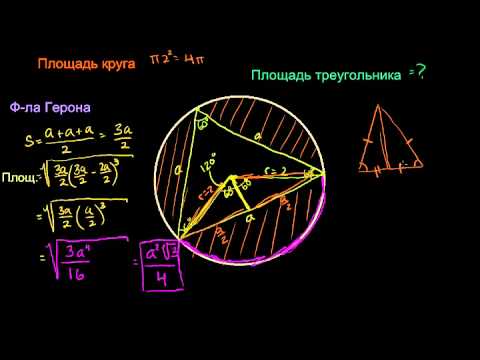
Те, кто помнит формула Герона, знают, как найти площадь этой фигуры. В процессе преобразования выражение изменится в представленное выше. Площадь этой фигуры по Герону рассчитывается так: 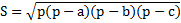
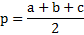
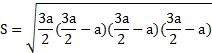
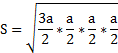
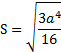
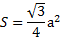
Полученная формула площади и представленные ниже функции могут быть использованы только, в случае, если фигура является правильной, в ином случае не будет давать правильный ответ.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Расчет по высоте
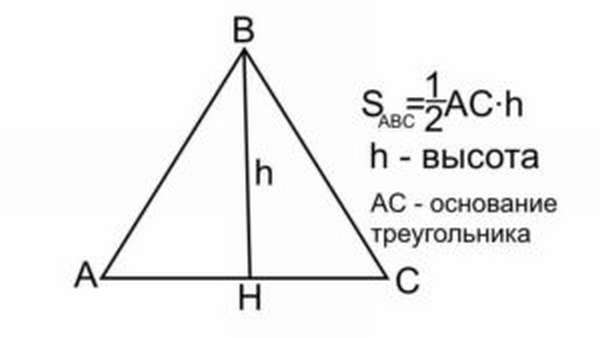
Найти площадь равностороннего треугольника можно также, если известна его высота и сторона. Половина длины высоты умножается на сторону, выбрана может быть любая высота и сторона, ведь согласно свойствам, они все одинаковые: 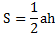
Если в задаче указана информация о том, что треугольник является равносторонним и известна величина высоты. А чему равна длина стороны неизвестно, то можно воспользоваться формулой, позволяющей ее рассчитать. Найти сторону можно разделив двойную величину высоты на корень квадратный из трех, математически выглядит следующим образом: 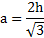
Для того чтобы не делать лишних расчетов можно вывести формулу этого показателя сразу же через высоту. Квадрат высоты делится на корень квадратный из трех. Она будет выглядеть так: 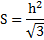
Видео:№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

Расчет через окружности
В математике популярен также прием расчета, рассматриваемого в статье, значения через помещение фигуры в окружность или наоборот. Такая окружность называется описанной. Если она находится внутри, то она называется вписанной. Именно в этом разделе возникает большинство вопросов, как найти площадь равностороннего многоугольника с тремя углами.
Описанная окружность обязательно должна проходить через все вершины, вписанная должна проходить через стороны только в одной точке по касательной.
Если в условии задачи дан радиус вписанной и описанной окружности, то из них также можно составить выражение, так как вместе они дадут суммарную длину высоты. Как рассчитывается площадь при ее помощи, показано выше: h = R + r .
Преобразовав формулу 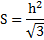
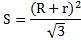
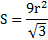
Если же будет дан размер радиуса описанной окружности, то выражение будет выглядеть следующим образом: 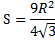
Использование этих свойств пригодится для расчета стороны фигуры. Для того чтобы ее найти можно воспользоваться выражением 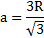
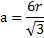
Учитывая радиус описанной окружности можно найти искомое значение при помощи возведения стороны в куб, после чего результат делится на радиус, увеличенный в 4 раза. Математически его можно записать следующим образом: 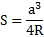
Процесс расчета, чему равен показатель площади равностороннего треугольника через любую из предложенных формул не должен вызывать особых затруднений. Для того чтобы успешно справиться с этой задачей не нужно запоминать все указанные способы, достаточно запомнить основные общие формулы расчета, а также свойства и признаки этой фигуры.
Внимание! Для проверки правильности расчетов можно воспользоваться несколькими способами, результаты должны совпасть.
Площадь равностороннего треугольника
Площадь равностороннего треугольника, вписанного в окружность
Применив логическое мышление, расчеты с легкостью преобразовываются в частные случаи, коих гораздо больше. Нецелесообразно забивать голову большим количеством нерелевантной информации, лучше развивать причинно-следственную связь для преобразования выражений.
Видео:КАК НАЙТИ ДЛИНУ ОКРУЖНОСТИ, ОПИСАННОЙ ОКОЛО ПРАВИЛЬНОГО ТРЕУГОЛЬНИКА? Примеры | ГЕОМЕТРИЯ 9 классСкачать

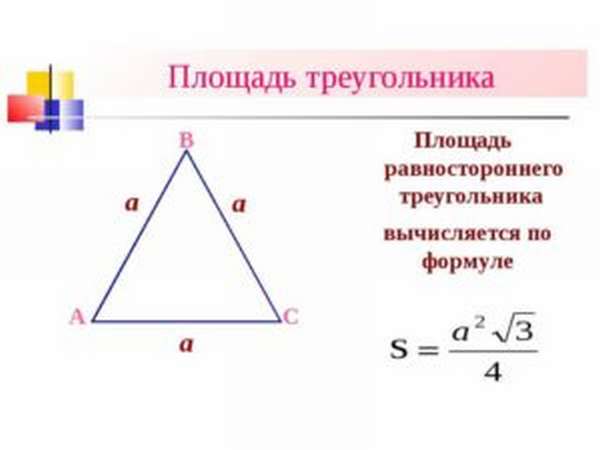
Правильный треугольник. Площадь правильного треугольника
Правильный треугольник — треугольник, у которого все стороны равны. Каждый угол правильного треугольника равен градусов.
Правильный треугольник называют еще равносторонним.
Каждая из высот правильного треугольника является также его медианой и биссектрисой.
Центры вписанной и описанной окружностей правильного треугольника совпадают.
Пусть сторона правильного треугольника равна .
Высота правильного треугольника:
Радиус окружности, вписанной в правильный треугольник: .
Радиус описанной окружности в два раза больше: .
Площадь правильного треугольника: .
Все эти формулы легко доказать. Если вы нацелены на решение задач части — докажите их самостоятельно.
. Сторона правильного треугольника равна . Найдите радиус окружности, вписанной в этот треугольник.
Задача решается в одну строчку. Радиус вписанной окружности .
. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна .
Сравним формулы для высоты правильного треугольника и радиуса вписанной окружности. Очевидно, радиус вписанной окружности равен высоты.
. Сторона правильного треугольника равна . Найдите радиус окружности, описанной около этого треугольника.
Радиус окружности, описанной вокруг правильного треугольника, равен .
Видео:Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать

Площадь правильного треугольника — формулы, свойства и признаки
Видео:112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписаннойСкачать

Формулы площади
правильного треугольника
- Формула площади правильного треугольника,
выраженная через сторону:
Формула площади правильного треугольника,
выраженная через периметр:
Формула площади правильного треугольника,
выраженная через радиус вписанной окружности:
Формула площади правильного треугольника,
выраженная через радиус описанной окружности:
Мы рассмотрели признаки, того что площадь в треугольнике является
площадью правильного треугольника, и рассмотрели формулы площади
характерные для правильного треугольника.
Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Признаки площади
правильного треугольника
Площадь в произвольном треугольнике, является площадью
правильного треугольника, если выполняется ряд признаков.
Например, если один из признаков правильного треугольника
истинен для произвольного треугольника, то площадь
можно найти по формулам истинным только для
правильного треугольника.
В правильном треугольнике все углы имеют градусную
меру в 60 градусов.Также, в правильном треугольнике
сумма градусных мер всех углов 180 градусов.
Перечислим основные признаки правильного треугольника:
- Все углы равны.
- Все стороны равны.
- Каждый угол по 60 градусов.
Если, для произвольного треугольника истинен один из
вышеперечисленных признаков, то треугольник правильный.
Соответственно, площадь в правильном треугольнике можно
найти, по формулам площади правильного треугольника.
📸 Видео
Треугольник и окружность #shortsСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

Геометрия 9 класс (Урок№22 - Формулы площади правильного многоугольника,стороны и радиуса впис.окр.)Скачать

Геометрия Площадь равностороннего треугольника, вписанного в окружность, равна Q^2 Доказать чтоСкачать

Площадь треугольника. Как найти площадь треугольника?Скачать

Геометрия Сторона равностороннего треугольника, вписанного в окружность равна a. Вычислить площадьСкачать

Площадь вписанного равностороннего треугольникаСкачать
Формулы для радиуса окружности #shortsСкачать

Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

Формулы радиусов описанной и вписанной окружностей правильного многоугольника 2Скачать

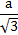 , а описанной согласно выражению R =
, а описанной согласно выражению R = 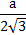 .
.


