Электрон движется по окружности сила эквивалентного тока (5 видео)

Электрон движется в однородном магнитном поле с индукцией 0,1 Тл по окружности

Содержание

Условие задачи:
Решение задачи:
Ответ: 1,76·10 10 рад/с.
Презентация к защите
Электрон движется по окружности сила эквивалентного тока
📹 Видео

Видео:Физика - Магнитное полеСкачать

Условие задачи:

Электрон движется в однородном магнитном поле с индукцией 0,1 Тл по окружности. Определить угловую скорость вращения электрона.

Задача №8.2.11 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Видео:Метод эквивалентного генератора МЭГ - Самое подробное объяснение задачиСкачать

Решение задачи:

На электрон, движущийся в магнитном поле, действует сила Лоренца (F_Л), которую определяет следующая формула:

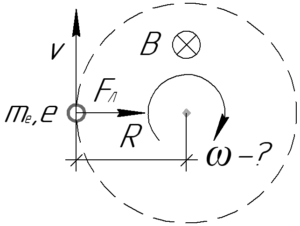
Здесь (B) – индукция магнитного поля, (upsilon) – скорость электрона, (e) – модуль заряда электрона, (alpha) – угол между вектором скорости и вектором магнитной индукции. Так как другого не сказано в условии, то (alpha=90^circ).

Направление действия силы Лоренца определяется правилом левой руки: если ладонь левой руки расположить так, чтобы линии магнитной индукции входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (или против направления отрицательного заряда, как в нашем случае), то большой палец, оставленный на 90°, покажет направление силы Лоренца. В нашем случае (при таком направлении вектора магнитной индукции) сила Лоренца направлена вправо.

Сила Лоренца (F_Л) сообщает электрону центростремительное ускорение (a_ц), поэтому из второго закона Ньютона следует, что:

Центростремительное ускорение (a_ц) можно определить через скорость (upsilon) и радиус кривизны траектории (R) по формуле:

Подставим (3) в (2), тогда:

Приравняем правые части (1) и (4):

Известно, что угловая скорость (omega) равна отношению линейной скорости (upsilon) к радиусу кривизны (R), поэтому:

[Besin alpha = omega ]

Выразим из этого уравнения искомую угловую скорость электрона (omega):

Масса электрона (m_e) равна 9,1·10 -31 кг, а его заряд (e) (вернее модуль заряда) равен 1,6·10 -19 Кл. Численный ответ равен:

Видео:Электротехника (ТОЭ). Лекция 9. Метод эквивалентного генератора | Решение задачСкачать

Ответ: 1,76·10 10 рад/с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Видео:Метод эквивалентного источникаСкачать

Презентация к защите

Магнитное поле движущегося электрического заряда

Электрон в невозбуждённом атоме водорода в соответствии с теорией Нильса Бора движется вокруг ядра по круговой орбите радиусом r @ 50 × 10 — 12 м. Вычислить силу эквивалентного кругового тока и напряжённость поля Н в центре окружности.

1. Электрон на стационарной круговой орбите находится, в соответствии с классической моделью атома, вследствие равенства по модулю силы Кулона, обусловленной электрическим взаимодействием электрона с ядром и силой инерции вызванной криволинейным его движением, сопровождающимся нормальным ускорением

, (1)

где e 0 @ 9 × 10 — 12 Ф/м — электрическая постоянная, е @ 1,6 × 10 — 19 Кл — заряд электрона, r — радиус орбиты электрона, me @ 1 × 10 — 30 кг — масса электрона.

2. Определим из равенства (1) скорость электрона v

. (2)

3. Частота вращения электрона вокруг ядра

. (3)

4. Сила тока по определению определяется в виде первой производной заряда, прошедшего через поперечное сечение по времени

. (4)

5. Модуль напряжённости магнитного поля, создаваемого вращающимся электрона определим, используя известные уравнения для магнитного поля кругового тока

. (5)

3.2.2. Определить максимальную магнитную индукцию Вmax поля, создаваемого электроном, движущимся по прямолинейной траектории со скоростью v = 10 Мм/с, в точке, отстоящей от траектории на расстоянии d = 1 × 10 — 9 м.

1. Определим величину эквивалентного тока I создаваемого движущимся электроном

, (1)

где е @ 1,6 × 10 — 19 Кл — заряд электрона.

2. Магнитная индукция будет иметь максимальную величину в момент прохождения электроном заданной точки

, (2)

в данном случае a 1 ® 0, a 2 @ 900, т.е.

. (3)

3.2.3. На расстоянии d = 10 нм от траектории прямолинейно движущегося электрона максимальное значение индукции составляет Вmax = 160 мкТл. Определить скорость электрона.

1. Для решения задачи воспользуемся уравнением (3) предыдущей задачи

. (1)

3.3. Сила, действующая на проводник с током

в магнитном поле

3.3.1. Прямолинейный проводник, по которому течёт постоянный ток силой I = 1000 A, расположен в однородном магнитном поле перпендикулярно линиям магнитной индукции. С какой силой F поле, характеризующееся индукцией В = 1 Тл действует на отрезок проводника длиной l = 1 м?

1. В соответствие с законом ампера сила, действующая на проводник с током в магнитном поле, определяется следующим векторным соотношением

, (1)

модуль силы Ампера

. (2)

2. В данном случае угол , откуда следует — . Сила, отнесённая к длине l = 1 м, определится в виде отношения

. (3)

ВОЛНОВЫЕ ПРОЦЕССЫ. ОПТИКА.

Волновой процесс. Характеристики волны. Волновое уравнение.

Представим себе цепочку, состоящую из равноотстоящих друг от друга материальных точек, которые связаны пружинками и могут движения, деформируя пружинки. Если сместить от положения равновесия какую-либо частицу, то она начнет совершать колебательное движение и, взаимодействуя через пружинки, вовлечет в колебания соседние частицы. Все частицы будут совершать колебания, тождественные с исходной, но не одновременно, а запаздывая по фазе. Таким образом, колебания будут распространяться в пространстве.

Если смещение от положения равновесия частицы с координатой 0 записать

, (3.1.1)

то для частицы с координатой х

————●///●///●///●///●———-х , (3.1.2)

х где – время, в течение которого

Рис.3.1.1 возмущение распространится от

источника до данной точки. Обозначим скорость распространения возмущения . Тогда и (3.1.2) перепишется . (3.1.3)

Величина – есть та разность фаз, на которую колебания точки на расстоянии х отстают по фазе от колебаний начальной точки. Аргумент косинуса – это фаза волны. Таким образом, фаза волны является функцией координат и времени.

Аналогичным образом процесс будет протекать в упругой среде, поскольку ее частицы взаимодействуют друг с другом похожим образом. Таким образом, процесс колебаний распространяется в пространстве. При этом необходимо отметить, что переноса вещества в пространстве не происходит, частицы среды лишь колеблются около положения равновесия. Распространение в пространстве различных видов возмущений вещества и поля, проявляющееся в переносе энергии возмущения, называется волновым процессом или волной. Если речь идет о колебаниях частиц среды, то волна называется упругой.

Видео:Электрическое поле. Напряженность электрического поля. Силовые линии электрического поля. 10 класс.Скачать

Электрон движется по окружности сила эквивалентного тока

электрон невозбужденном атоме водорода

Электрон в невозбужденном атоме водорода движется вокруг ядра по окружности радиуса r = 0,53·10 –8 см. Вычислить магнитный момент р_м эквивалентного кругового тока и механический момент М, действующий на круговой ток, если атом помещен в магнитное поле с индукцией В = 0,1 Тл, направленной параллельно плоскости орбиты электрона.

Принимая, что электрон в невозбужденном атоме водорода движется по круговой орбите радиусом r = 52,8 пм, определите: 1) магнитный момент р_m эквивалентного кругового тока; 2) орбитальный механический момент L_e электрона; 3) исходя из полученных числовых значений, гиромагнитное отношение орбитальных моментов, доказав, что оно совпадает со значением, определяемым универсальными постоянными.

Электрон в невозбужденном атоме водорода движется вокруг ядра по окружности радиусом r = 53 пм. Вычислить силу эквивалентного кругового тока I и напряженность H поля в центре окружности.

Фотон с энергией ε = 16,5 эВ выбил электрон из невозбужденного атома водорода. Какую скорость v будет иметь электрон вдали от ядра атома?

Фотон с энергией Е = 6,5 эВ выбил электрон из невозбужденного атома водорода (то есть электрон в атоме водорода находился на 1-ой боровской орбите). Какую скорость будет иметь выбитый электрон?

Фотон, соответствующий длине волны 0,015 мкм, выбил электрон из невозбужденного атома водорода. Вычислить скорость электрона за пределами атома.

Электрон в невозбужденном атоме водорода получил энергию 12,1 эВ. На какой энергетический уровень он перешёл? Сколько линий спектра могут излучиться при переходе электрона на более низкие энергетические уровни?