- 5. ДВИЖЕНИЕ ЭЛЕКТРОНОВ В ОДНОРОДНОМ МАГНИТНОМ ПОЛЕ.
- Шаг винтовой линии электрона
- §14. Движение заряженных частиц в электрическом и магнитном полях
- 14.3 Движение по винтовой линии в однородном магнитном поле.
- Движение электрона
- Содержание
- 1. Движение электрона в равномерном магнитном поле, неизменном во времени и направленном перпендикулярно скорости……………………..3
- Время одного оборота
- 🎬 Видео
Видео:Урок 276. Сила Лоренца. Движение заряженных частиц в магнитном полеСкачать

5. ДВИЖЕНИЕ ЭЛЕКТРОНОВ В ОДНОРОДНОМ МАГНИТНОМ ПОЛЕ.
В некоторых электровакуумных приборах используется движение электронов в магнитном поле.
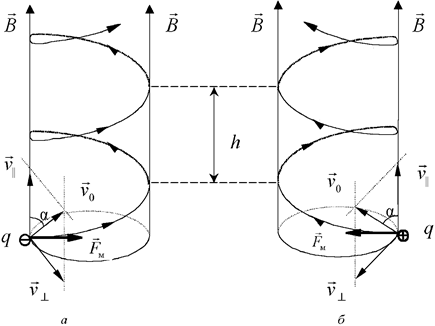
Рассмотрим случай, когда электрон влетает в однородное магнитное поле с начальной скоростью v0, направленной перпендикулярно магнитным силовым линиям. В этом случае на движущийся электрон действует так называемая сила Лоренца F, которая перпендикулярна вектору нО и вектору напряженности магнитного поля Н. Величина силы F определяется выражением: F= еv0Н.
При v0 = 0 сила Рравна нулю, т. е. на неподвижный электрон магнитное поле не действует.
Сила F искривляет траекторию электрона в дугу окружности. Поскольку сила F действует под прямым углом к скорости нО, она не совершает работы. Энергия электрона и его скорость не изменяются по величине. Происходит лишь изменение направления скорости. Известно, что движение тела по окружности (вращение) с постоянной скоростью получается благодаря действию направленной к центру центростремительной силы, которой именно и является сила F.
Направление поворота электрона в магнитном поле в соответствии с правилом левой руки удобно определяется по следующим правилам. Если смотреть в направлении магнитных силовых линий, то электрон движется по часовой стреле. Иначе говоря, поворот электрона совпадает с вращательным движением винта, который ввинчивается по направлению магнитных силовых линий.
Определим радиус r окружности, описываемой электроном. Для этого воспользуемся выражением для центростремительной силы, известным из механики: F = mv20/r. Приравняем его значению силы F = еv0Н: mv20/r = еv0Н. Теперь из этого уравнения можно найти радиус: r= mv0/(еН).
Чем больше скорость электрона v0, тем сильнее он стремится двигаться прямолинейно по инерции и радиус искривления траектории будет больше. С другой стороны, с увеличением Н растет сила F, искривление траектории возрастает и радиус окружности уменьшается.
Выведенная формула справедлива для движения в магнитном поле частиц с любыми массами и зарядом.
Рассмотрим зависимость rот mи е. Заряженная частица с большей массой mсильнее стремится лететь по инерции прямолинейно и искривление траектории уменьшится, т. е. rстанет больше. А чем больше заряд е, тем больше сила F и тем сильнее искривляется траектория, т. е. ее радиус становится меньше.
Выйдя за пределы магнитного поля, электрон дальше летит по инерции по прямой линии. Если же радиус траектории мал, то электрон может описывать в магнитном поле замкнутые окружности.
Таким образом, магнитное поле изменяет только направление скорости электронов, но не ее величину, т. е. между электроном и магнитным полем нет энергетического взаимодействия. По сравнению с электрическим полем действие магнитного поля на электроны является более ограниченным. Именно поэтому магнитное поле применяется для воздействия на электроны значительно реже, нежели электрическое поле.
Видео:Физика - движение по окружностиСкачать

Шаг винтовой линии электрона
Электрон, ускоренный разностью потенциалов U = 6 кВ, влетает в однородное магнитное поле под углом α = 30° к направлению поля и движется по винтовой траектории. Индукция магнитного поля B = 13 мТл. Найти радиус R и шаг h винтовой траектории.
Дано:
U = 6 кВ = 6·10 3 В
В = 13 мТл = 13 ·10 -3 Тл
Решение:
Разложим вектор скорости ν частицы на две составляющие (рис.): v 1 , направленную вдоль линий магнитной индукции, и v2, перпендикулярную этим линиям. Модули этих составляющих – соответственно υ 1 = ν cos α и v 2 = υ sin α
На частицу действует сила Лоренца, обусловленная со ставляющей v 2 . Вследствие этого частица движется по окружности со скоростью v 2 в плос кости, перпендикулярной магнитному полю. Радиус этой окружности определим, составив уравнение на основании второго закона Ньютона.
По второму закону Ньютона F Л = m е a, где a = υ 2 / R – центростремительное ускорение.
Скорость найдем из закона сохранения энергии
Одновременно частица будет двигаться и вдоль поля. Это равномерное движение со скоростью v 1 , так как состав ляющая v 1 не вызывает появления силы Лоренца. В ре зультате одновременного движения по окружности и по прямой частица будет двигаться по винтовой линии, «навиваясь» на линии магнитной индукции. Шаг винтовой линии
где Т — период обращения частицы по окружности:
получаем шаг винтовой линии
Ответ:
Заряд q влетает со скоростью 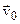
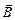
Рис. 12.7. Траектория движения заряда в магнитном поле:
а – отрицательный заряд; б – положительный заряд
Уравнение движения электрона определяется II законом Ньютона (12.1) с учетом магнитной силы (11.9)
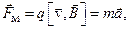
где q – заряд электрона.
Разложим скорость на составляющие, направленные параллельно и перпендикулярно вектору 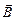
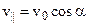
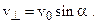
При движении электрона со скоростью 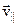
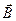
При движении электрона со скоростью 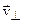
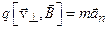
или, в скалярном виде,
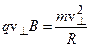
электрон будет двигаться по окружности радиусом
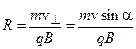
В результате сложения этих двух движений электрон будет двигаться по винтовой линии радиусом R и шагом винта h:
где T – период движения по окружности:
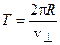
Таким образом получаем, что шаг винта будет равен:
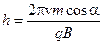
1. Как будет двигаться заряженная частица, влетевшая в однородное магнитное поле под углом в вектору 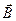
2. Если заряженная частица, пролетая некоторую область про-
странства, не отклоняется от первоначального направления движения, можно ли утверждать, что магнитное поле в этой области пространства отсутствует?
3. Протон и электрон, имеющие одинаковую скорость, попадают в однородное магнитное поле, индукция которого В перпендикулярна скорости зарядов. Как будут отличаться траектории заряженных частиц?
4. Чему равна работа силы, действующей на электрон, движущийся в однородном магнитном поле с индукцией В?
5. Покажите, что какой бы скоростью ни обладал электрон, влетающий в однородное магнитное поле с индукцией В, и каков бы ни был угол α между векторами 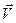
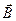
6. Какова форма траектории электрона, движущегося в совпадающих по направлению электрическом и магнитном полях, в случаях, когда: 1) начальная скорость электрона направлена вдоль полей, 2) скорость электрона перпендикулярна к Е и В?
7. Можно ли определить, каким полем вызвано отклонение пучка протонов, попавшего в некоторую область пространства, – электрическим или магнитным?
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Как то на паре, один преподаватель сказал, когда лекция заканчивалась – это был конец пары: «Что-то тут концом пахнет». 8526 – 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Видео:Движение заряженной частицы в магнитном поле | Физика ЕГЭ с Никитой АрхиповымСкачать

§14. Движение заряженных частиц в электрическом и магнитном полях
14.3 Движение по винтовой линии в однородном магнитном поле.
Рассмотрим теперь произвольный случай движения заряженной частицы в однородном магнитном поле.
Введем систему декартовых координат, так, чтобы вектор индукции однородного магнитного поля (
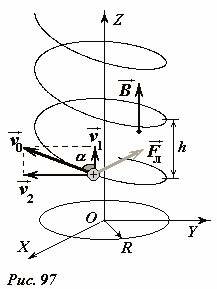
vec B) был направлен вдоль оси Oz (рис. 97). Пусть вектор скорости (
vec upsilon_0) частицы массы m, имеющей электрический заряд q, направлен под произвольным углом α к вектору индукции поля. Разложим этот вектор на две составляющих[
vec upsilon_1] – параллельную вектору индукции и (
vec upsilon_2) – перпендикулярную ему. Действующая на частицу сила Лоренца (
vec F_L) перпендикулярна векторам скорости и индукции, то есть лежит в плоскости xOy. Модуль этой силы равен
F_L = q upsilon_0 B sin alpha = q upsilon_2 B) . (1)
Если спроецировать уравнение второго закона Ньютона для частицы
m vec a = q vec upsilon imes vec B) , (2)
на плоскость xOy, то получим уравнение, в которое только компонента скорости, перпендикулярная полю. Это уравнение описывает движение частицы, движущейся перпендикулярно вектору индукции, которое было подробно рассмотрено ранее. Оно представляет собой равномерное движение по окружности радиуса
и угловой скоростью
не зависящими, ни от модуля скорости частицы, ни от ее направления.
Проекция магнитной силы на ось Oz равна нулю, поэтому проекция скорости на эту остается постоянной. Следовательно, эта координата изменяется по линейному закону
z = z_0 + upsilon_1 t = z_0 + upsilon_0 t cos alpha) . (6)
Таким образом, движение частицы можно представить в виде суперпозиции равномерного движения вдоль оси Oz и равномерного движения по окружности в перпендикулярной плоскости. Траекторией этого движения является винтовая линия, радиус которой определяется формулой (3), а шаг рассчитывается по формуле
h = upsilon_1 t = 2 pi frac cos alpha) . (7)
Таким образом, заряженные частицы движутся по спиралям (точнее винтовым линиям), навивающимся на силовые линии магнитного поля. Такой же характер движения сохраняется и в неоднородном магнитном поле – частицы движутся по спиралям, навивающимся на силовые линии поля, при этом радиус и шаг спирали плавно изменяются с изменением индукции поля. Направление смещения (дрейфа) частиц в магнитном поле определяется направлением начальной скорости частиц и не зависит ни от знака заряда частицы, ни от направления вектора индукции поля, последние определяют только направление вращения вокруг силовой линии. Такое движение заряженных частиц позволяет конструировать различные «магнитные ловушки» для накопления заряженных частиц, управлять движением сильно ионизованного газа (плазмы). Аналогичный характер имеет движение заряженных частиц и в магнитном поле Земли.
Видео:Движение электронов в магнитном поле - Сила ЛоренцаСкачать

Движение электрона
Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Содержание
Видео:Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

1. Движение электрона в равномерном магнитном поле, неизменном во времени и направленном перпендикулярно скорости……………………..3
2. Движение электрона в неизменном во времени магнитном поле, когда скорость электрона не перпендикулярна силовым линиям……………….4
3. Фокусировка пучка электронов постоянным во времени
магнитным полем (магнитная линза)……………………………………….6
4. Движение электронов в равномерном электрическом поле. Принцип работы электронного осциллографа………………………………………. 7
5. Фокусировка пучка электронов постоянным во времени
электрическим полем (электрическая линза)……………………………….8
6. Движение электрона в равномерных, взаимно перпендикулярных, неизменных во времени магнитном и электрическом полях………………9
7. Движение заряженных частиц в кольцевых ускорителях………………11
Движение заряженных частиц в магнитном и электрическом полях
1. Движение электрона в равномерном магнитном поле, неизменном во времени и направленном перпендикулярно скорости.
В данных разделах под заряженной частицей мы будем подразумевать электрон. Заряд его обозначим q=-qэ и массу m. Заряд примем равным qэ=1,601.10-19 Кл, при скорости движения, значительно меньшей скорости света, масса m=0,91.10-27 г. Полагаем, что имеет место достаточно высокий вакуум, так что при движении электрон не сталкивуается с другими частицами. На электрон, движущийся со скоростью 


На рис 1 учтено, что заряд электрона отрицателен, и скорость его 


Электрон будет двигаться по окружности радиусом r с угловой частотой ωц, которую называют циклотронной частотой. Центробежное ускорение равно силе f, деленной на массу 

Видео:Движение свободных электронов в металлахСкачать

Время одного оборота

2. Движение электрона в неизменном во времени магнитном поле, когда скорость электрона не перпендикулярна силовым линиям.
Рассмотрим два случая: в первом — электрон будет двигаться в равномерном, во втором – в неравномерном поле.
а) Движение в равномерном поле. Через α на рис 2. Обозначен угол между скоростью электрона 














Поступательное и одновременно вращательное движение иногда называют дрейфом электрона.
б) Движение в неравномерном поле. Если магнитное поле неравномерно, например сгущается ( рис.2 в.), то при движении по спирали электрон будет попадать в точки поля, где индукция В увеличивается. Но чем больше индукция В, тем при прочих равных условиях меньше радиус спирали r. Дрейф электрона будет происходить в этом случае по спирали со всем уменьшающимся радиусом. Если бы
магнитные силовые линии образовывали расходящийся пучок, то электрон при своем движении попадал бы в точки поля со все уменьшающейся индукцией и радиус спирали возрастал бы.
3. Фокусировка пучка электронов постоянным во времени магнитным полем (магнитная линза).
Из катода электронного прибора (рис. 3) выходит расходящийся пучок электронов. Со скоростью 
Разложим скорость электрона 


Первая 




4. Движение электронов в равномерном электрическом поле. Принцип работы электронного осциллографа.
Электрон, пройдя расстояние от катода К до узкого отверстия в аноде А (рис. 4, а), под действием ускоряющего напряжения Uак увеличивает свою кинетическую энергию на величину работы сил поля.
Скорость 
При дальнейшем прямолинейном движении по оси х электрон попадает в равномерное электрическое поле, напряженностью Е между отклоняющими пластинами 1 и 2 (находятся в плоскостях, параллельных плоскости zох).
Напряженность Е направлена вдоль оси у. Пока электрон движется между отклоняющимися пластинами, на него действует постоянная сила Fy = —qэE. направленная но оси —у. Под действием этой силы электрон движется вниз равноускоренно, сохраняя постоянную скорость 
5. Фокусировка пучка электронов постоянным во времени электрическим полем (электрическая линза).
Фокусировка основана на том что, проходя через участок неравномерного электрического поля, электрон отклоняется в сторону эквипотенциали с большим значением потенциала (рис. 5, а). Электрическая линза образована катодом, испускающим электроны, анодом, куда пучок электронов приходит сфокусированным, и фокусирующей диафрагмой, представляющей собой пластинку с круглым отверстием в центре (рис. 5, б). Диафрагма имеет отрицательный потенциал по отношению к окружающим ее точкам пространства, вследствие этого эквинотенциали электрического поля как бы выпучиваются через
диафрагму по направлению к катоду. Электроны, проходя через отверстие в диафрагме и отклоняясь в сторону, фокусируются на аноде.
6. Движение электрона в равномерных, взаимно перпендикулярных, неизменных во времени магнитном и электрическом полях.
Пусть электрон с зарядом q= —qэ, и массой т с начальной скоростью 




Уравнение движения 
Следовательно, 
В соответствии с формулой (2) заменим qэB/m на циклотронную частоту ωц. Тогда


Продифференцируем (4) по t и в правую часть уравнения подставим (5).

Решим уравнение классическим методом: vy=vy пр+vy св :
Составим два уравнения для определения постоянных интегрирования.
Так как при t=0 vy=v, то 




Таким образом,
Пути, пройденные электроном по осям у и z:

На рис. 6, б, в, г изображены три характерных случая движения при различных значениях v0. На рис. 6, б трохоида при v0=0, максимальное отклонение по оси z равно 
Если v0>0 и направлена по оси +y, то траекторией является растянутая
трохоида (рис. 6, в) с максимальным отклонением 
🎬 Видео
Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Движение заряженной частицы в магнитном поле 2021-1Скачать

Движение электрона в магнитном поле.Скачать

Лучшая модель атома? [Минутка физики]Скачать
![Лучшая модель атома? [Минутка физики]](https://i.ytimg.com/vi/eybcxXiYJfc/0.jpg)
Физика 9 класс (Урок№4 - Движение тела по окружности. Период и частота)Скачать

потомучто Откуда электрон берет энергию чтобы вечно вращаться вокруг ядраСкачать
Движение заряженных частиц Лекция 9-2Скачать

Атом:Загадка Электронов. Квантовая механика.Скачать

Движение электронов в атоме. 1 часть. 8 класс.Скачать

55. Движение частиц в электромагнитных поляхСкачать

Положительно заряженная частица в магнитном и электрическом поле. Выполнялка 36Скачать

Пучок электронов в магнитном полеСкачать

Теория движения заряженных частиц в электрическом поле .Часть 1Скачать