Две окружности с центрами в точках o и o1

Условие

Две окружности с центрами O1 и O1 пересекаются в точках А и В, причем точки О1 и О2 лежат по разные стороны от прямой АВ. Продолжение диаметра СА первой окружности и хорды СВ этой же окружности пересекает вторую окружность в точках D и E соответственно.

а) Докажите, что треугольники CBD и O1AO2 подобны.

б) Найти AD, если углы DAE и BAC равны, радиус второй окружности в четыре раза больше радиус первой и АВ=2.

Видео:Две окружности с центрами О1 и О3 и радиусами 7 и 6 касаютсяСкачать

Окружность. Относительное взаимоположение окружностей.

Если две окружности имеют только одну общую точку, то говорят, что они касаются.

Если же две окружности имеют две общие точки, то говорят, что они пересекаются.

Трех общих точек две не сливающиеся окружности иметь не могут, потому, что в противном случае через три точки можно было бы провести две различные окружности, что невозможно.

Будем называть линией центров прямую, проходящую через центры двух окружностей (например, прямую OO₁).

Теорема.

Если две окружности имеют общую точку по одну сторону от линии центров, то они имеют общую точку и по другую сторону от этой линии, т.е. такие окружности пересекаются.

Пусть окружности O и O₁ имеют общую точку A, лежащую вне линии центров OO_1. Требуется доказать, что эти окружности имеют еще общую точку по другую сторону от прямой OO₁.

Опустим из A на прямую OO₁ перпендикуляр AB и продолжим его на расстояние BA₁, равное AB. Докажем теперь, что точка A₁ принадлежит обеим окружностям. Из построения видно, что точки O и O₁ лежат на перпендикуляре, проведенном к отрезку AA₁ через его середину. Из этого следует, что точка O одинаково удалена от A и A₁. То же можно сказать и о точке O₁. Значит обе окружности, при продолжении их, пройдут через A₁.Таким образом, окружности имеют две общие точки : A (по условию) и A₁ (по доказанному). Следовательно, они пересекаются.

Следствие.

Общая хорда (AA₁) двух пересекающихся окружностей перпендикулярна к линии центров и делится ею пополам.

Теоремы.

1. Если две окружности имеют общую точку на линии их центров или на ее продолжении, то они касаются.

2. Обратно: если две окружности касаются, то общая их точка лежит на линии центров или на ее продолжении.

Признаки различных случаев относительного положения окружностей.

Пусть имеем две окружности с центрами O и O₁, радиусами R и R₁ и расстоянием между центрами d.

Эти окружности могут находиться в следующих 5-ти относительных положениях:

1. Окружности лежат одна вне другой, не касаясь. В этом случае, очевидно, d > R + R₁ .

2. Окружности имеют внешнее касание. Тогда d = R + R₁, так как точка касания лежит на линии центров O O₁.

3. Окружности пересекаются. Тогда d R + R₁, потому что в треугольнике OAO₁ сторона OO₁ меньше суммы, но больше разности двух других сторон.

4. Окружности имеют внутреннее касание. В этом случае в d = R — R₁, потому что точка касания лежит на продолжении линии OO₁.

5. Одна окружность лежит внутри другой, не касаясь. Тогда, очевидно,

d R + R₁, то окружности расположены одна вне другой, не касаясь.

2. Если d = R + R₁, то окружности касаются извне.

3. Если d R — R₁, то окружности пересекаются.

4. Если d = R — R₁, то окружности касаются изнутри.

5. Если d R Е R₁. Значит, все эти случаи исключаются. Остается один возможный, именно тот, который требовалось доказать. Таким образом, перечисленные признаки различных случаев относительно положения двух окружностей не только необходимы, но и достаточны.

Видео:Геометрия Две окружности с центрами O1 и O3 и радиусами 4,5 и 2,5 касаются друг с другом внешнимСкачать

Две окружности с центрами О1 и О2, радиусы у которых равны пересекаются в точках M и N, через точку М проведена прямая параллельной О1О2 и пересекающая окружность с центром О2 в точке Д?

Геометрия | 5 — 9 классы

Две окружности с центрами О1 и О2, радиусы у которых равны пересекаются в точках M и N, через точку М проведена прямая параллельной О1О2 и пересекающая окружность с центром О2 в точке Д.

Используя переллельный перенос докажите , что четырехугольник О1МДО2 является параллелограммом.

О1М и О2Д — радиусы равных окружностей.

Следовательно, они равны.

Опустив перпендикуляры Ма из М и Дн из Д на прямую О1О2, получим равные между собой отрезки, ониравные также высоте четырехугольника О1О2ДМ.

Прямоугольные треугольники О1аМ и О2нД равны по гипотенузе и катету, и их основания лежат на одной прямой.

Сдвигая окружность О1 по прямой О1О2, получим совмещениеО1 и О2, т.

Совпадут и перпендикулярные отрезки между прямыми, опущенные из точек пересечения радиусов с окружностью.

Расстояние между их вершинами М и Д, О1 и О2 равны.

Следовательно, МД = О1О2.

Четырехугольник, в котором стороны попарно равны и параллельны, — параллелограмм

Четырехугольник О1МДО2 является параллелограммом, что и требовалось доказать.

Видео:Геометрия Окружности с центрами в точках O1 и O2 не имеют общих точек. Внутренняя общая касательнаяСкачать

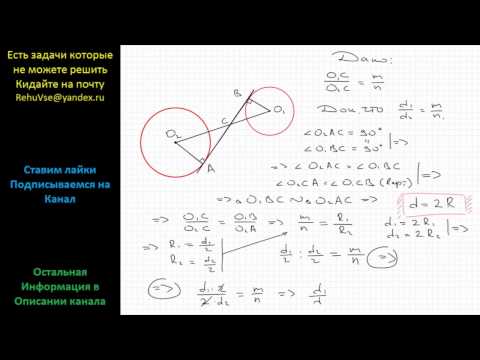
Докажите что если две окружности с центрами О и О1 пересекаются в точках А и В, то АВ _|_ ОО1?

Докажите что если две окружности с центрами О и О1 пересекаются в точках А и В, то АВ _|_ ОО1.

Видео:Г: Три равные окружности с центрами О1, О2, О3 и радиусом R попарно касаются друг друга в точках А ВСкачать

Диагонали ромба «abcd» пересекаются в точке «о» ?

Диагонали ромба «abcd» пересекаются в точке «о» .

Докажите , что прямая «bd» касается окружности с центром «а» и радиусом , равным «ос».

Видео:ОГЭ Задание 25 Две окружностиСкачать

Диагонали ромба АВСD пересекаются в точке О?

Диагонали ромба АВСD пересекаются в точке О.

Докажите, что прямая BD касается окружности с центром А и радиусом, равным ОС.

Видео:Задача по темам: окружность, равнобедренный треугольник. "Окружности с центрами в точках Р и Q ..."Скачать

Две окружности с равными радиусами пересекаются в двух точках?

Две окружности с равными радиусами пересекаются в двух точках.

Докажите, что их общая хорда перпендикулярна к отрезку, соединяющему центры окружностей.

Видео:Геометрия Две окружности радиуса R с центрами O1 и O2 касаются друг друга. Их пересекает прямаяСкачать

Докажите, что прямая, проходящая через центр окружности, пересекает окружность в двух точках?

Докажите, что прямая, проходящая через центр окружности, пересекает окружность в двух точках.

Видео:ОГЭ по математике. Окружности с центрами. 1 Вар.Скачать

Две окружности равных радиусов пересекаются в точках А и В?

Две окружности равных радиусов пересекаются в точках А и В.

Докажите, что отрезок, соединяющий центры окружностей, перпендикулярен АВ.

Видео:Теорема о числе точек пересечения двух окружностейСкачать

Через точку А к окружности проведены касательная АБ и секущая, которая пересекает окружность в точках E и F и проходит через центр окружности?

Через точку А к окружности проведены касательная АБ и секущая, которая пересекает окружность в точках E и F и проходит через центр окружности.

Найдите радиус окружности если AB = 12, а AF = 18.

Видео:Геометрия Две окружности пересекаются в точках A и B. Через точку A проведены диаметры AC и AD этихСкачать

Окружности радиусов 4 и 3, расстояние между центрами которых равно 5, пересекаются в точках А и В?

Окружности радиусов 4 и 3, расстояние между центрами которых равно 5, пересекаются в точках А и В.

Через точку В проведена прямая, пересекающая большую окружность в точке С, а меньшую в точке D ( точка В лежит между С и D).

Опредилите косинусы углов треугольника АСD.

Видео:Два кольца из разных проводников с центрами в точках O1 и O2 соединены, как показано на рисункеСкачать

Через концы диаметра AB окружности с центром О, проведены параллельные прямые, пересекающие окружность в точках М и К?

Через концы диаметра AB окружности с центром О, проведены параллельные прямые, пересекающие окружность в точках М и К.

Докажите, что МК — диаметр окружности.

С рисунком, пожалуйста!

Видео:№675. Стороны угла О касаются каждой из двух окружностей, имеющих общую касательную в точке АСкачать

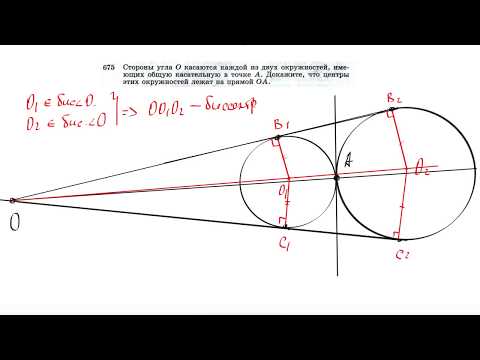
Две окружности пересекаются в точках P и Q?

Две окружности пересекаются в точках P и Q.

Через точку A первой окружности проведены прямые AP и AQ, пересекающие вторую окружность в точках B и C.

Докажите, что касательная в точке A к первой окружности параллельна прямой BC.

На странице вопроса Две окружности с центрами О1 и О2, радиусы у которых равны пересекаются в точках M и N, через точку М проведена прямая параллельной О1О2 и пересекающая окружность с центром О2 в точке Д? из категории Геометрия вы найдете ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

📺 Видео

9.52.1. Планиметрия. Гордин Р.К.Скачать

ЕГЭ Задание 16 Три окружностиСкачать

10.19.1. Планиметрия. Гордин Р.К.Скачать

Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

Два кольца из разных проводников с центрами в точках O1 и O2 соединены, как показано на рисунке.Скачать

2023 На окружности с центром в точке О отмечены точки А и Б так что угол аоб равен 45Скачать

Геометрия В точках пересечения двух окружностей с радиусами 4 и 8 см касательные к ним взаимноСкачать

Г: Две окружности касаются друг друга внешним образом в точке С. Радиусы окружностей равны 2 и 7Скачать